Мы начнем с простой игры, которая называется Квадраты. Игра начинается с произвольного целого неотрицательного числа (скажем, 75). Два игрока по очереди вычитают из него натуральные числа, являющиеся полными квадратами (то есть 1, 4, 9, 16, 25 и т.д.), так чтобы оставшееся число было неотрицательным. Проигрывает тот, кто не может сделать очередной ход. Вот как, например, может протекать игра:

75 50 46 30 5 4 0

На этом рисунке ходы первого игрока изображены красной стрелкой, а ходы второго — зеленой. Мы видим, что в приведенном примере второй игрок выиграл, поскольку у первого нет больше допустимых ходов. Но возникает сомнение: играл ли первый игрок достаточно хорошо? Мог ли он выиграть, действуй он по-другому? Если бы оба игрока играли наилучшим образом, с каким результатом закончилась бы эта партия?

Предположим, что игра начинается с неотрицательного числа n. Возможны два исхода:

  1. первый игрок имеет стратегию, позволяющую ему выиграть при любых действиях второго; 
  2. такой стратегии у первого игрока нет, поэтому второй всегда может выиграть.

В случае (a) будем называть число n выигрышным, а в случае (b) — проигрышным.

Давайте разберем простые примеры.
  1. 0 — безусловно проигрышное число, потому что в этой позиции нельзя сделать ни одного хода.
  2. Любой полный квадрат — 1, 4, 9, 16, ... — выигрышное число, потому что можно за один ход превратить его в ноль, предложив противнику проигрышную позицию.
Путем несложных рассуждений можно заполнить такую таблицу:

Таблица 1

0

1

2

3

4

5
     

где череп с костями символизируют проигрышную позицию, а пустые клетки соответствуют выигрышным позициям. Можно сформулировать правило, по которому заполняется такая таблица:

Если первый игрок может сделать ход и попасть в проигрышную позицию, то изначальная позиция — выигрышная.
В противном случае, любая позиция, в которую можно сделать ход, — выигрышная, и поэтому изначальная позиция  — проигрышная.


Если вы задумаетесь на мгновение над этим правилом, оно станет для вас очевидным. Действительно, вы хотите, чтобы ваш соперник проиграл, поэтому вы должны оставить ему проигрышную позицию. Если вы не сможете этого сделать, то проиграете вы сами.

Чтобы дать вам почувствовать, как все это работает, мы продолжили таблицу 1 и заполнили ее для всех n вплоть до 21. Вот что у нас получилось:

Таблица 2

0

1

2

3

4

5

6

7

8

9

10
           

 

11

12

13

14

15

16

17

18

19

20

21
             

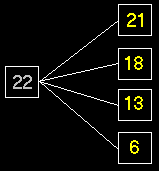
Теперь мы хотим проанализировать число 22. В этой позиции возможны 4 разных хода:


Каждое из четырех полученных чисел — 6, 13, 18, 21 — выигрышное. Поэтому само число 22  — проигрышное. Таким способом мы можем легко исследовать любую начальную позицию в этой игре.



Как сделать правильный ход

Мало просто знать, что позиция, в которой вы оказались — выигрышная. Надо еще суметь сделать правильный ход.

 

Пример 1. Начальная позиция: n=19. Какой первый ход нужно сделать?

Решение. Взгляните на таблицу 2. Число 19 — выигрышное. Для победы нам необходимо выбрать такой ход, после которого сопернику достанется проигрышная позиция. У нас всего 4 варианта: 18, 15, 10 и 3. Вновь обратимся к таблице 2, и выберем из наших четырех чисел проигрышные. Нам подходят числа 15 и 10: любой из этих ходов оставит сопернику проигрышное число.

Пример 2. Из начального числа n=18 первый игрок вычел 4, оставив сопернику число 14. Что делать дальше?

Решение. И вновь воспользуемся таблицей 2. Мы видим, что 14 — выигрышное число (первый игрок сделал не самый лучший ход!). Поэтому у второго игрока появилась возможность выиграть партию. Для этого ему нужно оставить первому игроку проигрышное число, например, 10. Победа!

Сейчас мы приведем более эффективный способ определения выигрышных и проигрышных позиций. Этот метод похож на решето Эратосфена, позволяющее находить все простые числа в заданном диапазоне. Предположим, что нам хочется определить исходы всех игр с начальными значениями от 0 до 15. мы знаем, что 0 — проигрышное число:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17
                                 

 

Добавляя к числу 0 квадраты, мы получаем числа 1, 4, 9, которые являются выигрышными, потому что из них можно попасть в проигрышное число 0:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17
                         

 

Самое маленькое непомеченное число — 2 — проигрышное, потому что иначе мы бы его уже пометили:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17
                       

 

Прибавляя к числу 2 квадраты, получаем новые выигрышные числа (2+1, 2+4, 2+9) :

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17
                 

 

Следующее непомеченное число — 5 — снова проигрышное. Продолжая так и далее, мы заполним всю таблицу:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

 


Выигрывай быстро, проигрывай медленно!

Пример 3. Представьте, что вам досталось начинать игру с проигрышного числа 17. Надежды нет?

Решение. Только без паники.  Теоретически, ваш противник имеет выигрышную стратегию. Но кто вам сказал, что он достаточно хорошо знает математику, и не сделает ошибки по ходу игры? Но представьте на минуту, что первым ходом вы вычитаете из 17 число 16 и оставляете сопернику 1. Тут уже ему ничего не остается, кроме как сделать последний победный ход. Значит, стоит оставлять число как можно большее? И это не так. Самое большое число, которое вы сможете оставить — 16. Но оно является полным квадратом, и второй игрок тут же оставит вам ноль. На самом деле, нужно оставлять такое число, чтобы для победы второму игроку оставалось как можно больше ходов до победы.

Будем называть удаленностью позиции n число, определяемое по следующим правилам:
  1. Если n=0, то удаленность равна 0.
  2. Если позиция n — выигрышная, то ее удаленность на 1 больше, чем наименьшая удаленность позиции, в которую можно попасть из n за один ход.
  3. Если позиция n — проигрышная, то ее удаленность на 1 больше, чем наибольшая удаленность позиции, в которую можно попасть из n за один ход.

Удаленность позиции характеризует количество ходов, необходимых для завершения партии. Приведенное выше правило основывается на простой идее. Игрок, имеющий выигрышную стратегию, стремится победить как можно быстрее, чтобы свести к минимуму возможность случайной ошибки при выборе очередного хода. Проигрывающий же старается как можно дольше оттягивать свое поражение, надеясь на оплошность соперника. Коротка эту стратегию можно сформулировать так:

ВЫИГРЫВАЙ БЫСТРО,
ПРОИГРЫВАЙ МЕДЛЕННО!

Продемонстрируем, как работает это правило. Пусть мы уже вычислили удаленности всех позиций до n=16, и теперь хотим узнать, чему же равна удаленность числа 17.

 

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17
0 1 2 3 1 2 3 4 5 1 4 3 6 7 3 4 1  

 

Из числа 17 можно получить числа 16, 13, 8 или 1. Их удаленности равны 1, 7, 5, 1 соответственно. Поскольку число 17 — проигрышное, его удаленность на 1 больше, чем наибольшая из удаленностей чисел 16, 13, 8, 1, то есть равна 7+1=8. Из проигрышного числа нужно всегда делать ход в то число, удаленность которого наибольшая возможная. В данном случае это число 13.

В завершение заметим, что нечетное значение удаленности соответствует выигрышным позициям, а четное — проигрышным.



Ним Витхоффа

Вот правила этой игры. Дана пара неотрицательных целых чисел (которые могут быть равны). Два игрока ходят по очереди. За один ход разрешается  (a) либо вычесть любое число из одного из данных, (b) либо вычесть из обоих данных чисел одно и то же число. При этом требуется, чтобы оба числа оставались неотрицательными. Проигрывает тот, кто не может сделать хода (то есть игрок, который оставляет своим ходом получает позицию (0,0), выигрывает).

Эта игра эквивалентна игре Ферзь Витхоффа, в которую играют на шахматной доске, на которой стоит изначально в клетке (n,m) стоит ферзь. За один ход разрешается передвинуть ферзя на любое количество клеток влево, вверх или влево-вверх. Выигрывает тот, кто приведет ферзя в клетку (0,0).


Мы можем проанализировать эту игру так же, как предыдущую.

11                    
10                    
9                    
8                    
7                    
6                    
5                    
4                    
3                    
2                    
1                    
0
  0 1 2 3 4 5 6 7 8 9 10 11



11              
10            
9            
8            
7            
6            
5            
4            
3              
2
1
0
  0 1 2 3 4 5 6 7 8 9 10 11



11        
10      
9    
8    
7      
6      
5
4          
3
2
1
0
  0 1 2 3 4 5 6 7 8 9 10 11


Продолжая так и далее, мы найдем проигрышные позиции (m, n) (m < n) : (0,0), (1,2), (3,5), (4,7), (6,10), (8,13), ... . Можно заметить и обобщить эту закономерность: чтобы найти (i+1)-ю проигрышную позицию, требуется найти наименьшее натуральное число k, которое не участвует в записи предыдущих позиций (ни на первом, ни на втором месте в паре). Искомая позиция —  (k, k+i).