Теоретический материал

Сайт:	Информатикс
Курс:	Динамическое программирование
Книга:	Теоретический материал

Напечатано::	Гость
Дата:	Понедельник, 18 Август 2025, 06:33

Введение
Некоторые обозначения и определения
Задача о замощении домино
Задача о симпатичных узорах
Связь ДП по профилю и линейной алгебры
Задача о расстановке королей
Задача о расстановке коней
ДП по изломанному профилю
Задачи, на которых можно потренироваться

Введение

К большинству олимпиадных задач ограничения (по времени, по памяти) жюри подбирает по принципу "как можно больше". То есть чтобы любые разумные реализации правильного решения проходили, а всё остальное -- нет.

Когда встречается задача с маленькими ограничениями (например, до 10), это означает, что либо автор намеренно сбивает Вас с правильного пути, либо действительно эта задача решается каким-то (оптимизированным) перебором.

Динамическое программирование по профилю -- одна из таких оптимизаций. Часто в таких задачах дело происходит на прямоугольной таблице, одна из размерностей которой достаточно мала (не более 10). Требуется проверить существование, посчитать количество способов, стоимость и т.д. (как в обычном динамическом программировании). Асимптотика алгоритма, основанного на этой идее, является экспоненциальной только по одной размерности, а по второй -- линейная или даже лучше.

Некоторые обозначения и определения

Матрицей размера n×m называется прямоугольная таблица n×m, составленная из чисел.

Обычно матрицы обозначают заглавными латинскими буквами. Элемент i-й строки j-го столбца матрицы A обозначают через a_ij или a[i, j] (соответствующая маленькая латинская буква с индексами).

Произведением двух матриц ${A \atop n \times m}$ и ${B \atop m \times k}$ называется матрица такая ${C \atop n \times k}$ , что

c_ij = $\displaystyle \sum_{t = 1}^{m}$ a_itb_tj.

(1)

В этом случае пишут: C = AB.

D в степени k (D^k), при условии, что D -- квадратная (т. е. n = m) определяется следующим образом:

D⁰ = E (единичная матрица), где

E = $\displaystyle \left(\vphantom{\begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \... ...dots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}}\right.$ $\displaystyle \begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \\ 0 & 1 & 0 & ... ...ots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \... ...dots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}}\right)$ .
На диагонали у нее стоят единицы, в остальных клетках -- нули. Она не зря называется единичной -- при умножении на нее матрица не изменяется: AE = EA = A.
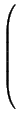
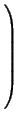Dⁱ = D^{i - 1}D, i > 0.

В приводимом коде будет использоваться функция bit(x,i), возвращающая единицу или ноль -- i-й бит в двоичной записи числа x (нумерация битов с нуля).

// возвращает i-й бит числа x, нумерация с нуля
function bit(x, i : integer) : integer;
begin
    if (i < 0) then bit := 0 else
        if (x and (1 shl i) = 0) then bit := 0 else bit := 1;
end;

Задача о замощении домино

Чтобы понять, что такое динамика по профилю, будем рассматривать разные задачи и разбирать их решения с помощью этого приема.

Для начала рассмотрим известную задачу: дана таблица n×m, нужно найти количество способов полностью замостить ее неперекрывающимися костяшками домино (прямоугольниками 2×1 и 1×2). Считаем n, m $\le$ 10.

Заметим, что в процессе замощения каждая клетка таблицы будет иметь одно из двух состояний: покрыта какой-нибудь доминошкой или нет. Чтобы запомнить состояние клеток одного столбца, достаточно одной переменной P типа integer. Положим i-й бит P равным 1, если i-я сверху клетка данного столбца занята, 0 -- если свободна. Будем говорить в таком случае, что P -- битовая карта нашего столбца.

Теперь дадим определение базовой линии и профиля.

Базовой линией будем называть вертикальную прямую, проходящую через узлы таблицы.

Можно занумеровать все базовые линии, по порядку слева направо, начиная с нуля. Таким образом, базовая линия с номером i -- это прямая, отсекающая первые i столбцов от всех остальных (если такие имеются).

Отныне через b_i будем обозначать базовую линию с номером i.

Столбцы занумеруем так: слева от b_i будет столбец с номером i. Другими словами, столбец с номером i находится между b_{i - 1} и b_i.

**Рисунок 1:** Профиль будет таким: 100101₂ = 1 + 4 + 32 = 37 (заняты первая + третья + шестая клетки).
$\begin{figure}\centering { \epsfbox{dprof/pic.1}} \end{figure}$

Профилем для базовой линии с номером i (b_i) будем называть битовую карту для столбца с номером i при следующих дополнительных условиях:

1): все клетки слева от b_{i - 1} уже покрыты;
2): в i-м столбце нет вертикальных доминошек;
3): считается, что справа от b_i нет покрытых клеток.

Первое условие возникает от желания считать количество способов постепенно, сначала рассматривая первый столбец, потом второй при условии, что первый уже заполнили и т.д. Второе и третье вводятся для того, чтобы один и тот же способ покрытия не был посчитан более одного раза. Точный смысл этих условий будет раскрыт ниже.

**Рисунок 2:** p₁ = 37, p₂ = 2; нетрудно заметить по рисунку, что из p₁ можно получить p₂. Таким образом, d[37, 2] = 1.
$\begin{figure}\centering { \epsfbox{dprof/pic.2}} \end{figure}$

Для каждого профиля p₁ базовой линии b_i определим множество профилей p₂ базовой линии b_{i + 1}, которые могут быть из него получены. На таблицу, соответствующую p₁ (то есть все клетки слева от b_{i - 1} полностью покрыты, в i-м столбце клетки отмечены согласно p₁), можно класть доминошки только двух типов:

1): горизонтальные доминошки, которые пересекают b_i (то есть делятся ей пополам);
2): вертикальные доминошки, которые лежат слева от b_i.

Также должны быть выполнены естественные дополнительные условия:

1): новые доминошки не должны перекрываться друг с другом;
2): они должны покрывать только незанятые клетки;
3): каждая клетка i-го столбца должна быть покрыта.

Битовая карта столбца i + 1 и будет возможным профилем p₂.

Очевидно, что полученный таким образом профиль p₂ действительно удовлетворяет всем условиям, накладываемым на профиль.

Пусть d[p₁, p₂] - количество способов из профиля p₁ (для b_i) получить p₂ (для b_{i + 1}). Очевидно, для данной задачи про доминошки это число может быть только единицей или нулем. Различные задачи будут отличаться в основном только значениями d[p₁, p₂].

Заметим, что всего профилей 2ⁿ: от 00...0₂ = 0 до 11...1₂ = 2ⁿ - 1. Поэтому в данном случае матрица D будет иметь размер 2ⁿ×2ⁿ.

Пусть теперь a[i, p] -- количество способов таким образом расположить доминошки, что p -- профиль для b_i (таким образом, все клетки левее b_{i - 1} покрыты).

Напишем рекуррентное соотношение.

Начальные значения (i = 1):
a[1, 0] = 1;
a[1, p₂] = 0, p₂ = 1, ..., 2ⁿ - 1
Общая формула (i > 1):

a[i, p₁] = $\displaystyle \sum_{p_2 = 0}^{2^n - 1}$ a[i - 1, p₂] d[p₂ p₁] (2)

Заметим, что для базовой линии номер 1 существует единственный профиль (то есть битовая карта, удовлетворяющая условиям профиля) -- карта незаполненного столбца.

Ответ на вопрос задачи будет записан в a[m + 1, 0]. Ошибкой бы было считать правильным ответом число a[m, 2ⁿ - 1], так как в этом случае не учитывается возможность класть вертикальные доминошки в последнем столбце (см. второй пример).

Обсудим "странные" условия на доминошки при получении одного профиля из другого. Казалось бы, забыт еще один тип доминошек, которые могут участвовать при формировании нового профиля, а именно полностью лежащие в столбце i + 1. Дело в том, что если разрешить их, то некоторые способы замощения будут считаться более одного раза. Например, пусть n = 2, m = 2. Тогда d'[0][3] = 2, так как можно положить либо две вертикальные доминошки, либо две горизонтальные. Аналогично, d'[3][3] = 1 (можно положить одну вертикальную). В итоге

D' = $\displaystyle \left(\vphantom{ \begin{array}{ccccccc} 1 & 0 & 0 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \end{array}}\right.$ $\displaystyle \begin{array}{ccccccc} 1 & 0 & 0 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccccccc} 1 & 0 & 0 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \end{array}}\right)$ , A' = $\displaystyle \left(\vphantom{ \begin{array}{ccccc} 1 & 1 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 2 \end{array}}\right.$ $\displaystyle \begin{array}{ccccc} 1 & 1 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 2 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccccc} 1 & 1 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 2 \end{array}}\right)$

Имеем неправильный ответ 3 (можно посчитать вручную, что на самом деле ответ 2).

Напротив, если следовать данному правилу получения из одного профиля другого, то можно убедиться в верности вычислений.

Упражнение. Доказать, что a[i, p] вычисляется правильно.

Вот какими будут D и A если n = 2, m = 4:

D = $\displaystyle \left(\vphantom{ \begin{array}{ccccccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}}\right.$ $\displaystyle \begin{array}{ccccccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccccccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}}\right)$ , A = $\displaystyle \left(\vphantom{ \begin{array}{ccccccccc} 1 & 1 & 2 & 3 & 5 \\ ... ...0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 2 & 3 \end{array}}\right.$ $\displaystyle \begin{array}{ccccccccc} 1 & 1 & 2 & 3 & 5 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 2 & 3 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccccccccc} 1 & 1 & 2 & 3 & 5 \\ ... ...0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 2 & 3 \end{array}}\right)$

Таким образом, замостить доминошками таблицу 2×4 можно 5 способами, а таблицу 2×2 -- двумя. Если смотреть a[m, 2ⁿ - 1], то получим 2 и 1. Очевидно, что таблицу 2×2 можно замостить двумя, а не одним способом: пропущен вариант, когда кладутся две вертикальные доминошки. В случае 2×4 пропущены три замощения -- все случаи, когда последний столбец покрыт вертикальной доминошкой.

Существует два способа для вычисления D. Первый заключается в том, чтобы для каждой пары профилей p₁ и p₂ проверять, можно ли из p₁ получить p₂ описанным способом.

При втором способе для каждого профиля p₁ пытаемся его замостить, кладя при этом только домоношки разрешенных двух типов. Для всех профилей p₂ (и только для них), которые при этом получались в следующем столбце, положим d[p1, p2]=1. В большинстве случаев этот способ более экономичный, так что логично использовать именно его.

Ниже приведен код рекурсивной процедуры, которая заполняет строку d[p], то есть находит все профили, которые можно получить из p:

procedure go(p, profile, len : integer);
begin
                                                // n - из условия задачи
                                                // profile - текущий профиль
                                                // len - длина profile
     if (len = n) then begin                    // как только profile получился длины n, выходим
        d[p][profile] := 1;
        exit;
    end;     
    if (bit(p, len) = 0) then begin             // текущая ячейка в p (с номером len + 1) не занята
        go(p, profile + (1 shl len), len + 1);  // положили горизонтальную доминошку
        if (len < n - 1) then
            if (bit(p, len + 1) = 0) then begin // не занята еще и следующая ячейка
                go(p, profile, len + 2);        // положили вертикальную доминошку
            end;     
        end else begin
            go(p, profile, len + 1);            // текущая ячейка занята, ничего положить не можем
        end;
    end;

procedure determine_D; 
var p : integer; 
begin   
    for p := 0 to (1 shl n) - 1 do
        go(p, 0, 0);                            // запускать надо именно с такими параметрами 
end;

Алгоритм вычисления D и A работает за

O(2²ⁿ) (вычисление D) + O(2²ⁿm) (вычисление A) = O(2²ⁿm).

Задача о симпатичных узорах

Рассмотрим еще одну задачу с прямоугольной таблицей.

Дана таблица n×m, каждая клетка которой может быть окрашена в один из двух цветов: белый или черный. Симпатичным узором называется такая раскраска, при которой не существует квадрата 2×2, в котором все клетки одного цвета. Даны n и m. Требуется найти количество симпатичных узоров для соответствующей таблицы.

**Рисунок 3:** Первые два узора симпатичные; у третьего и четвертого есть полностью черный и, соответственно, белый квадратик 2×2.
$\begin{figure}\centering { \epsfbox{dprof/pic.5}} \end{figure}$

Будем считать профилем для b_i битовую карту i-го столбца (единицей будет кодировать черную клетку, а нулем -- белую). При этом узор, заключенный между нулевой и i-й базовыми линиями, является симпатичным.

Из профиля p₁ для b_i можно получить p₂ для b_{i + 1}, если и только если можно так закрасить (i + 1)-й столбец, что его битовая карта будет соответствовать p₂, и между b_{i - 1} и b_{i + 1} не будет полностью черных либо белых квадратиков 2×2.

**Рисунок 4:** На левом рисунке p₁ = 1 + 4 + 32 = 37, p₂ = 2 + 8 + 16 = 26; так как между b_{i - 1} и b_{i + 1} не встречаются одноцветные квадратики 2×2, то p₂ может быть получен из p₁. На рисунке справа p₁ также равно 37, а p₂ = 1 + 2 + 4 = 7.
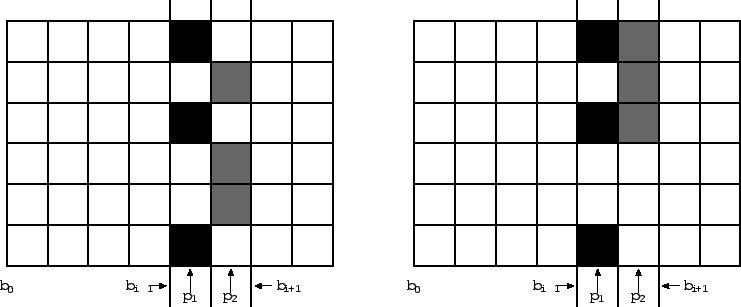$\begin{figure}\centering { \epsfbox{dprof/pic.6} } \end{figure}$

Сколькими же способами из одного профиля можно получить другой? Понятно, что закрасить нужным образом либо можно, либо нельзя (так как раскрашивать можно единственным образом -- так, как закодировано в p₂). Таким образом, d[p₁, p₂] $\in$ {0, 1}.

Вычислять D можно либо проверяя на "совместимость" (то есть наличие одноцветных квадратов 2×2) все пары профилей, либо генерируя все допустимые профили для данного. Ниже приведен код, реализующий первую идею:

// можно ли из p1 получить p2
function can(p1, p2 : integer) : boolean;
var i : integer;
    b : arrray[1..4] of byte;
begin
    for i := 0 to n - 2 do begin
        b[1] := bit(p1, i);
        b[2] := bit(p1, i + 1);
        b[3] := bit(p2, i);
        b[4] := bit(p2, i + 1);

        if (b[1] = 1) and (b[2] = 1) and (b[3] = 1) 
                               and (b[4] = 1) then begin
            // квадрат в строках i и i + 1 черный
            can := false;
            exit;
        end;

        if (b[1] = 0) and (b[2] = 0) and (b[3] = 0) 
                               and (b[4] = 0) then begin
            // квадрат в строках i и i + 1 белый
            can := false;
            exit;
        end;
    end;
    can := true;    
end;

procedure determine_D;
var p1, p2 : integer;
begin
    for p1 := 0 to (1 shl n) - 1 do
        for p2 := 0 to (1 shl n) - 1 do
            if can(p1, p2) then d[p1, p2] :=1
            else d[p1, p2] := 0;
end;

После того, как вычислена матрица D, остается просто применить формулу (2) (так как расуждения на этом этапе не изменяются).

Связь ДП по профилю и линейной алгебры

Рекуррентное соотношение (2) будет встречаться нам не только в задаче о замощении или симпатичном узоре, но и во многих других задачах, решаемых динамикой по профилю. Поэтому логично, что существует несколько способов вычисления A, используя уже вычисленную D (а не только наивно пo (2)). В этом пункте мы рассмотрим способ, основанный на возведении в степень матрицы:

1): a[i] можно считать матрицей 1×2ⁿ;
2): D -- матрица 2ⁿ×2ⁿ;
3): a[i] = a[i - 1]D. Если расписать эту формулу по определению произведения, то получится в точности (2).

Следуя определению степени матрицы, получаем

a[m] = a[0]D^m

(3)

Вспомним, как возвести действительное число a в натуральную степень b за O(log b) (считaем, что два числа перемножаются за O(1)). Представим b в двоичной системе счисления: b = 2^i₁ + 2^i₂ +...+ 2^i_k, где i₁ < i₂ <...< i_k. Тогда k = O(log b). Заметим, что a^2ⁱ получается из a^{2^{(i - 1)}} возведением последнего в квадрат. Таким образом, за O(k) можно вычислить все a^p_t, p_t = 2^i_t, t = 1, ..., k. Перемножить их за линейное время тоже не представляет труда.

Логично предположить, что аналогичный алгоритм сгодится и для квадратных матриц. Единственное нетривиальное утверждение -- A^2ⁱ = (A^{2^{i - 1}})², ведь по определению A^2t = 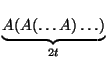$\underbrace{A(A(\dots A)\dots)}_{2t}^{}\,$ , а мы хотим приравнять его к (A^t)(A^t). Его истинность следует из ассоциативности умножения матриц (AB)C = A(BC). Само свойство можно доказать непосредственно, раскрыв скобки в обеих частях равенства.

Приведем код процедуры возведения в степень (функция mul перемножает две квадратные матрицы размера w × w):

function mul(a, b : tmatr) : tmatr;
var res : tmatr;
    i, j, t : integer;
begin
    for i := 1 to w do begin
        for j := 1 to w do begin
            res[i][j] := 0;
            for t := 1 to w do begin
                res[i][j] := res[i][j] + a[i][t]*b[t][j];
            end;
        end;
    end;
    mul := res;
end;

function power(a : tmatr; b : integer) : tmatr;
var i, j : integer;
    res, tmp : tmatr;
begin
    res := E; // единичная матрица
    tmp := a;
    while (b > 0) do begin
        if (b mod 2 = 1) then res := mul(res, tmp);
        b := b div 2;
        tmp := mul(tmp, tmp);
    end;
    power := res;
end;

Как уже говорилось, будет сделано O(log b) перемножений. В данном случае, на каждое перемножение тратится n³ операций (где n -- размерность матрицы). Так что этот алгоритм будет работать за O(n³log b).

Вернемся к (3). Матрицу D мы умеем вычислять за O((2ⁿ)²n) = O(4ⁿn) (как в рассмотренных задачах). Вектор a[m] сумеем найти за O((2ⁿ)³log b) = O(8ⁿlog m). В итоге получаем асимптотику O(8ⁿlog m). При больших m (например, 10¹⁰⁰) этот способ вычисления A несравнимо лучше наивного.

Задача о расстановке королей

Дана шахматная доска n×m и число k. Нужно посчитать количество способов размещения на этой доске k королей так, чтобы они не били друг друга.

Профилем опять будет битовая карта столбца слева от базовой линии. В данном случае удобно запоминать расположение королей. Таким образом, единица будет означать наличие короля на соответствующей позиции. При переходе от одного профиля к другому ставим королей справа от b_i так, чтобы они не били друг друга и предшествующих им.

Заметим, что снова d_ij $\in$ {0, 1}. Отличие этой задачи от предыдущих заключается в следующем. Количество "настоящих" профилей сильно отличается от 2ⁿ: если в позиции j есть король, то в позициях j - 1 и j + 1 его заведомо нет. То есть, в двоичной записи профиля не должно встречатся двух подряд идущих единиц. Пусть f (n) -- количество возможных профилей длины n.

Напишем для f (n) рекуррентную формулу. Количество профилей, у которых на n-м месте стоит 1, равно f (n - 2), так как на (n - 1)-м не может стоять 0, на остальные ячейки ограничений нет. Если же на n-м месте стоит 0, то количество будет равно f (n - 1). Тогда f (n) = f (n - 1) + f (n - 2); f (1) = 2, f (2) = 3. Получили, что f (n) -- (n+2)-е число Фибоначчи. Известно, что f (n) < (1, 62)^{n + 2}. При n = 10 имеем f (n) = 144 против количества битовых карт 1 024, уменьшение более чем в 7 раз!

Использовать это наблюдение можно по-разному.

Будем рассматривать только настоящие профили (при вычислении D и A), используя рекурсию:

procedure go(len, profile : integer);
begin
    // profile - текущий профиль
    // len = (длина profile) + 1
    
    if (len > n) then begin
        // как только profile получился длины n, выходим
        writeln(profile, ' - настоящий профиль');
        exit;
    end;

    go(len + 1, profile*2);
    // приписать ноль мы всегда можем

    if (profile mod 2 = 0) then 
                 go(len + 1, profile*2 + 1);
    // приписать единицу можно только если рядом ноль
end;

procedure print_all_true_profiles;
begin
  go(1, 0); //запускать надо именно с такими параметрами
end;

Занумеруем все настоящие профили так, чтобы быстро получать по номеру профиль. Тогда чтобы перебрать все настоящие профили, нужно будет пустить цикл по номеру с 1 до их количества f (n), и каждый раз находить профиль по текущему номеру. Например, можно брать номера в лексикографически упорядоченном списке профилей (чтобы сказать, какой из двух профилей больше лексикографически, достаточно сравнить их как числа).
Пусть p -- настоящий ненулевой профиль. Если заменить в нем произвольную единичку (в двоичной записи) на нолик, то получится тоже настоящий профиль. Другими словами, если убрать короля, то ничего плохого не будет. Аналогично, если в p заменить 0 на 1, чтобы не возникло двух подряд идущих единиц, результатом будет настоящий профиль.
На этом основан еще один способ получения всех настоящих профилей: "поиском в ширину". Из настоящих профилей, в котоых ровно i королей, получаем всевозможные настоящие профили из i + 1 королей.
```
var use : array[0..(1 shl n) - 1] of byte; 
   // use[p] = 1, если p - в очереди
   q : array[1..(1 shl n)] of integer; // очередь
   r : integer; // итоговое количество настоящих профилей

procedure determine_all_true_profiles;
var i, l, x, y : integer;
begin
    l := 0;
    r := 1;
    for i := 1 to (1 shl n) - 1 do use[i] := 0;
    use[0] := 1;
    q[1] := 0;
    while (l < r) do begin
        l := l + 1;
        x := q[l];
        // теперь попробуем подобавлять единички
        for i := 0 to n - 1 do
            if (bit(x,i) = 0) and (bit(x, i - 1) = 0) 
                       and (bit(x, i + 1) = 0) then begin
                y := x + (1 shl i);
                if (use[y] = 0) then begin
                    r := r + 1;
                    q[r] := y;
                end;
            end;
    end;
end;
```
После завершения работы процедуры в очереди q будут содержаться все настоящие профили.

В итоге при использовании нашего наблюдения получаем асимптотику O(m(f (n))²)

Задача о расстановке коней

На этот раз на шахматной доске n×n нужно подсчитать количество способов расставить k коней так, чтобы они не били друг друга.

Мы уже привыкли, что профиль -- битовая карта столбца левее b_i. Но здесь этой информации мало, так как кони могут прыгать сразу через два столбца. Поэтому профиль должен описывать два соседних столбца.

Для двух профилей pr₁ = $\langle$ p₁, p₂ $\rangle$ (p₁ -- битовая карта первого столбца, p₂ -- второго) и pr₂ = $\langle$ p'₁, p'₂ $\rangle$ положим d[pr₁, pr₂] = 1 если и только если

a): p₂ = p'₁;
б): кони не бьют друг друга.

В противном случае d[pr₁, pr₂] = 0.

Таким образом, переходов на порядок меньше, чем количество профилей. Всего профилей 4ⁿ, а из каждого профиля получается менее 2ⁿ новых за счет совпадения p₂ и p₁'. Другими словами, матрица D сильно разрежена (имееет много нулевых элементов).

Поэтому в задаче о расстановки коней можно добиться значительного ускорения (по сравнению с шаблонным алгоритмом), если хранить D в виде "списков смежности": D'[pr₁] -- список всех таких pr₂, из которых можно получить pr₁, то есть d[pr₂][pr₁] = 1. В этом случае формула (2) будет выглядеть так:

a[i, p] = $\displaystyle \sum_{t \in D'[p]}^{}$ a[i - 1, t] d[t, p].

Суммарное время вычисления a[i] равно количеству всевозможных переходов, то есть количество ненулевых элементов в D. В нашем случае (задаче о конях) их не более 4ⁿ×2ⁿ = 8ⁿ, то есть время работы алгоритма с такой оптимизацией будет O(8ⁿm) -- это в 2ⁿ раз меньше, чем время стандартного алгоритма.

ДП по изломанному профилю

Другое название этому методу -- "быстрая динамика по профилю". Идея в том, чтобы добиться как можно меньшего числа переходов (от одного профиля к другому).

**Рисунок 5:** Изображение профиля $\langle$ 33, 2 $\rangle$ ( 33 = 2⁰ + 2⁵).
$\begin{figure}\centering { \epsfbox{dprof/pic.3} } \end{figure}$

Еще раз используем в качестве примера задачу о замощении. Базовая линия теперь будет ломаной: при прохождении через i-ю горизонталь сверху вниз, она переходит на предыдущую вертикаль и спускается до низу (см. рис. 5).

Профилем будет пара $\langle$ p, i $\rangle$ , в p будет информация о n + 1 маленьком квадратике слева от базовой линии, имеющем с ней общие точки; i обозначает номер горизонтали, на которой произошел излом. Квадратики профиля будут нумероваться сверху вниз, так что угловой будет иметь номер i + 1. Горизонтали будем нумеровать нуля, так что i пробегает значения 0..n - 1.

Для двух профилей pr₁ = $\langle$ p₁, i₁ $\rangle$ и pr₂ = $\langle$ p₂, i₂ $\rangle$ положим d[pr₁][pr₂] = 1 если и только если:

а): если i < n - 1, то i₁ + 1 = i₂; иначе i₂ = 0;
б): можно так положить доминошку, накрывающую (i + 1)-й квадратик, что после этого в p₂ будет храниться в точности информация о соответствующих квадратиках.

Проще говоря, доминошку можно класть только двумя способами -- как показано на рисунках (на (i + 1)-й квадратик можно положить не более одной вертикальной и горизонтальной доминошки). То, что потом получается после сдвига вниз излома, и будет новым профилем. Заметим, что если (i + 1)-я клетка занята, то доминошку уже не надо класть, и $\langle$ p, i $\rangle$ логично отождествить с $\langle$ p, i + 1 $\rangle$ ("i + 1" пишется условно, нужно всегда иметь в виду возможность i = n - 1).

Легко заметить, что количество профилей увеличилось в 2n раз (добавилось число от 1 до n и еще один бит). Но зато количество переходов резко сократолсь с 2ⁿ до двух!

В нижеприведенном куске кода для профиля $\langle$ p, i $\rangle$ выводятся все переходы из него (напомним, что нумерация горизонталей начинается с нуля и i = 0..n - 1):

procedure print_all_links(p, i : integer);
begin
    if (bit(p, i + 1) = 0) then begin
        if (i = n - 1) then begin
            writeln('<', (p - (2 shl i)) shl 1, ', ', 0, '>');
        end else begin
            writeln('<', p - (2 shl i), ', ', i + 1, '>');
        end;
    end else begin
        if (bit(p, i) = 0) then begin
            if (i = n - 1) then begin
                writeln('<', p shl 1, ', ', 0, '>');
            end else begin  writeln('<', p + (1 shl i), ', ', 
                            (i + 1) mod n, '>');         end;
        end;
        if (i < n - 1) and (bit(p , i + 2) = 0) then begin
            writeln('<', p + (4 shl i), ', ', i + 1, '>');
        end;
    end;
end;

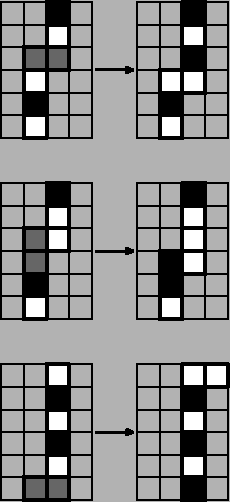
$\epsfbox{dprof/pic.4}$

Рисунок 6. Возможные переходы.

При такой реализации существует немало профилей только с одним переходом (например, у которых (i + 1)-й бит равен единице).

Отождествим все профили с один переходом с теми, кто их них получается. Это будет выглядеть так: пусть pr₂ (и только он) получается из pr₁, который, в свою очередь, получается из pr₀. Тогда имеются такие соотношения: d[pr₀, pr₁]=1, d[pr₁, pr₂]=1. Отождествить pr₁ и pr₂ -- это, по сути, заменить эти два соотношение на одно, то есть теперь d[pr₀, pr₁]=0 и d[pr₁, pr₂]=0, но d[pr₀, pr₂]=1, и так далее.

Таким образом, возможно сокращение профилей не менее чем вдвое. Дальнейшие оптимизации мы оставляем читателю.

В итоге получаем асимптотику 2ⁿn (количество переходов, то есть время на вычисление a[i]) умножить на m равно O(2ⁿnm). Она значительно лучше всего, что мы получали до сих пор, и это серьезный повод использовать изломанный профиль вместо обычного.

Задачи, на которых можно потренироваться

Cайт http://acm.sgu.ru, задачи 131, 132, 197, 223, 225.
Московская олимпиада по информатике, 2004 год, заочный тур, задача J ("Узор"),
http://www.olympiads.ru/moscow/2004/zaoch/problems.shtml