Теоретический материал: алгоритм Карацубы и быстрое преобразование Фурье (А.Климовский)
| Сайт: | Информатикс |
| Курс: | Арифметика и числовые алгоритмы |
| Книга: | Теоретический материал: алгоритм Карацубы и быстрое преобразование Фурье (А.Климовский) |
| Напечатано:: | Гость |
| Дата: | Пятница, 27 Февраль 2026, 11:29 |
Длинная арифметика возвращается
А. Климовский
С детства нас учат умножать в столбик, но при выступлениях на олимпиадах высокого уровня, приходит понимание, что эффективности этого алгоритма не всегда хватает. Весь дальнейший материал будет в основном исследовать алгоритмы умножения чисел и многочленов.
Алгоритм Карацубы
Идея, сложность
Алгоритм по своей сути рекурсивный и основывается на сведении задачи перемножения многочленов степени 2n к трем задачам умножения многочленов степени n:
![]() (1)
(1)
Вычисляются перемножением многочлены ![]() ,
, ![]() ,
, ![]() . Последний в свою очередь равен
. Последний в свою очередь равен ![]() . Таким образом, вычитанием найдем и второе выражение в правой части формулы (1).
. Таким образом, вычитанием найдем и второе выражение в правой части формулы (1).
Оценим получающуюся сложность
![]() , где в
, где в ![]() включены все производимые вычитания и сложения многочленов.
включены все производимые вычитания и сложения многочленов.
Итого, как это строго доказано в [1], ![]()
Реализация, оптимизации
С реализацией проблем возникнуть не должно. Ключевой оптимизацией является использование «наивного» алгоритма для маленьких значений n. Это значение, после которого n называется «маленьким» зависит от разных факторов. В качестве упражнения рекомендуется дома его узнать для своего компьютера, а также для популярных тестирующих систем on-line. Еще в реализациях часто используется много операций копирования, обнуления и выделения памяти. Это вполне можно свести к минимуму.
Приведем отрывки кода (взятые из авторского решения первой из разбираемых задач), достаточно оптимально реализующего описанный алгоритм на языке Delphi.
type tpoly=array [0..MaxD] of integer;
ppoly=^tpoly;
procedure add (var a:tpoly; const b:tpoly; bd:integer; const c:tpoly; cd:integer);
var i:integer;
begin
for i:=0 to min (bd, cd) do
a[i]:=b[i]+c[i];
if bd<cd then
move (c[bd+1], a[bd+1], (cd-bd)*sizeof (integer))
else
move (b[cd+1], a[cd+1], (bd-cd)*sizeof (integer))
end;
procedure mul (var a:tpoly; const b, c:tpoly; d:integer);
var i, j, k:integer;
x, y, z:array of integer;
begin
if d<50 then begin
for i:=0 to d do
for j:=0 to d do
inc (a[i+j], b[i]*c[j]);
exit;
end;
k:=d shr 1 + 1;
mul (a, b, c, k-1);
mul (ppoly (@a[k shl 1])^, ppoly (@b[k])^, ppoly (@c[k])^, d- k);
setlength (x, k);
add (ppoly (@x[0])^, b, k-1, ppoly (@b[k])^, d-k);
setlength (y, k);
add (ppoly (@y[0])^, c, k-1, ppoly (@c[k])^, d-k);
setlength (z, (k-1) shl 1 + 1);
mul (ppoly (@z[0])^, ppoly (@x[0])^, ppoly (@y[0])^, k-1);
sub (ppoly (@z[0])^, ppoly (@z[0])^, (k-1) shl 1, ppoly (@a[0])^, (k-1) shl 1);
sub (ppoly (@z[0])^, ppoly (@z[0])^, (k-1) shl 1, ppoly (@a[k shl 1])^, (d-k) shl 1);
add (ppoly (@a[k])^, ppoly (@a[k])^, (k-1) shl 1, ppoly (@z[0])^, (k-1) shl 1);
end;
Видно, что этот код довольно некрасив, и хотя идейно прост, может уйти много времени на написание и отладку. К сожалению, здесь нельзя сказать, что такие оптимизации обычно не нужны, потому что если в задаче требуется алгоритм Карацубы, то ограничения чаще всего достаточно жесткие.
И напоследок не забудьте про то, что числа ― это не совсем многочлены. Типичной ошибкой является неправильный выбор основания системы счисления. Основание системы счисления, которое не вызовет переполнение используемых типов в некоторых реализациях может зависеть от длины перемножаемых чисел. Рекомендуется избегать таких реализаций, это возможно без больших потерь производительности.
Дискретное преобразование Фурье
Введение (комплексные числа, комплексная экспонента, корни из единицы и прочие простые сущности из математики)
При обсуждении вопросов преобразования Фурье нам понадобятся некоторые факты. Коротко:
Поле комплексных чисел ![]() (само понятие поля вовсе не нужно)
(само понятие поля вовсе не нужно)
Комплексная экспонента ![]()
Корни из единицы (решения уравнения ![]() ) ― это множество
) ― это множество ![]()
Многочлены
Многочлен ― это функция вида ![]()
По значениям многочлена в (n+1)-ой различной точке, он восстанавливается однозначно. Например, по формуле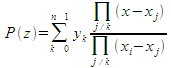 (интерполяционный многочлен Лагранжа)
(интерполяционный многочлен Лагранжа)
Дискретное преобразование Фурье (формальное определение, терминология)
Определение. Дискретным преобразованием Фурье называется преобразование последовательности ![]() в последовательность
в последовательность ![]() по формуле:
по формуле:
![]()
Примечание. В литературе также встречаются определения, отличающиеся от указанного наличием знака «минус» в экспоненте, а так же коэффициентом перед всем выражением.
Как несложно заметить, это есть значения многочлена в корнях из единицы.
Обратное преобразование
Обратное преобразование, как несложно доказать, записывается в виде
![]()
Если прямое преобразование обозначить за ![]() (представляя его как оператор, действующий на столбец), то
(представляя его как оператор, действующий на столбец), то ![]() . Можно так же его выразить через перестановки последовательностей, это не сложно.
. Можно так же его выразить через перестановки последовательностей, это не сложно.
Алгоритм Cooley-Tukey
Рассмотрим случай, когда ![]() . Так как для многочленов это всегда можно сделать, дополнив нулями в конце, не будем останавливаться на других случаях. В теории рассмотрим только прямое преобразование, а при реализации учтем оба варианта.
. Так как для многочленов это всегда можно сделать, дополнив нулями в конце, не будем останавливаться на других случаях. В теории рассмотрим только прямое преобразование, а при реализации учтем оба варианта.
Основная идея ― разбить сумму на половину слагаемых с четными номерами и половину с нечетными. Построим для них преобразованные последовательности. Обозначим указанные последовательности ![]() и
и ![]() для четных номеров,
для четных номеров, ![]() и
и ![]() для нечетных (
для нечетных (![]() ).
).
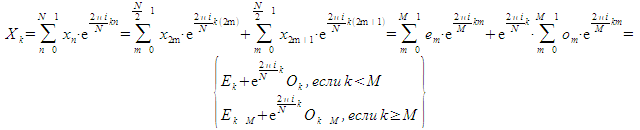
Теперь всё готово для рекурсивной реализации преобразования, это предлагается сделать в качестве домашнего задания. Далее же рассмотрим, как избавиться от рекурсии и получить большую эффективность.
Для этого посмотрим, какие будут рекурсивные вызовы, например, при ![]() :
:
(0, 1, 2, 3, 4, 5, 6, 7)
(0, 2, 4, 6) (1, 3, 5, 7)
(0, 4) (2,6) (1, 5) (3, 7)
(0) (4) (2) (6) (1) (5) (3) (7)
Теперь если мы будем иметь конечную перестановку и за каждую из ![]() итераций будем объединять попарно участки, как описано выше, то получим в итоге преобразование Фурье.
итераций будем объединять попарно участки, как описано выше, то получим в итоге преобразование Фурье.
Несложно понять и доказать, что конечный порядок является реверсом битов (bit-reversal permutation), то есть числа упорядочены по «перевернутым» битам. Это следует из того, что на каждом этапе рекурсивного спуска выделяются четные и нечетные половины, соответствующие числам с соответствующим битом 0 или 1. Эта перестановка получается, например, методом «перевернутого» бинарного счетчика за линейное время.
Разбор реализации
Вот пример более-менее эффективного кода (взят из открытых источников и проверен). Здесь не вводится класс комплексных чисел, а все хранится в одном массиве. На четных местах ― вещественные части, а нечетных ― мнимые. Так же код универсальный для прямого и обратного преобразования.
//nn должно быть степенью двойки!!!
procedure FastFourierTransform(var a : Array of Double; nn : Integer; InverseFFT : Boolean);
var
ii, jj, n, mmax, m, j, istep, i, isign : Integer;
wtemp, wr, wpr, wpi, wi, theta, tempr, tempi : Double;
begin
if InverseFFT then isign := -1
else isign := 1;
n := 2*nn;
j := 1;
ii:= 1;
while ii<=nn do begin
i := 2*ii-1;
if j>i then begin
tempr := a[j-1];
tempi := a[j];
a[j-1] := a[i-1];
a[j] := a[i];
a[i-1] := tempr;
a[i] := tempi;
end;
m := n div 2;
while (m>=2) and (j>m) do begin
j := j-m;
m := m div 2;
end;
j := j+m;
Inc(ii);
end;
mmax := 2;
while n>mmax do begin
istep := 2*mmax;
theta := 2*Pi/(isign*mmax);
wpr := -2.0*sqr(sin(0.5*theta));
wpi := sin(theta);
wr := 1.0;
wi := 0.0;
ii:=1;
while ii<=mmax div 2 do begin
m := 2*ii-1;
jj:=0;
while jj<=(n-m) div istep do begin
i := m+jj*istep;
j := i+mmax;
tempr := wr*a[j-1]-wi*a[j];
tempi := wr*a[j]+wi*a[j-1];
a[j-1] := a[i-1]-tempr;
a[j] := a[i]-tempi;
a[i-1] := a[i-1]+tempr;
a[i] := a[i]+tempi;
Inc(jj);
end;
wtemp := wr;
wr := wr*wpr-wi*wpi+wr;
wi := wi*wpr+wtemp*wpi+wi;
Inc(ii);
end;
mmax := istep;
end;
if InverseFFT then
for I := 0 to 2*nn-1 do
a[I-1] := a[I-1]/nn;
end;
Подключение к длинной арифметике
Для умножения двух многочленов нужно представить их в виде своих значений в корнях из 1, перемножить эти значения, а потом восстановить многочлен по значениям. Из показанного выше следует, что это легко сделать тремя преобразованиями Фурье (двумя прямыми и одним обратным). Единственное, где можно ошибиться – это неправильно задать количество точек. Оно должно соответствовать степени не только исходных многочленов, но и степени их произведения.
Для перемножения длинных чисел нужно не забыть про переходы через разряд, а также про ограничение на основание системы счисления, связанное с «переполнением» мантиссы вещественного числа.
Разбор задач
В рассматриваемых задачах БПФ (или алгоритм Карацубы) используется не как вспомогательный инструмент для длинной арифметики, а для перемножения многочленов, которое может быть видно не сразу. Это обусловлено тем, что задачи на длинную арифметику сами не представляют теоретического интереса.
Летние учебно-тренировочные сборы кандидатов в сборную России по информатике, Малоярославец, 27 июня 2006 года
Задача A. Дырявая лента
Имя входного файла
holytape.in
Имя выходного файла
holytape.out
Ограничение по времени
10 секунд
Ограничение по памяти
64 мегабайта
За сверхполезные исследования в области просвета ключей, содержащих прямоугольные дырки, руководство НИИ Исследований Данных Строк присудило Васе специальную премию. Вдохновленный полученными результатами и поддержкой руководства, Вася решил пойти дальше и попробовать на просвет другие объекты. И вот, он держит в руках две древние телетайпные ленты!
Каждая телетайпная лента – это бесконечная в обе стороны лента бумаги. Начиная с некоторого места, на ленте дырочками закодировано сообщение. Сообщение состоит из K позиций, представленных на ленте ячейкой 1 × 1 сантиметр каждая. Ширина ленты составяет 3 сантиметра.
В каждой из позиций ленты, отвечающей за кодирование сообщения, либо есть дырочка (тогда соответствующий бит сообщения равен единице), либо нет (в этом случае бит равен нулю). Если в соседних позициях есть дырочки, то они сливаются.
Например, если сообщение выглядело как 01110010111011, то лента будет выглядеть таким образом:
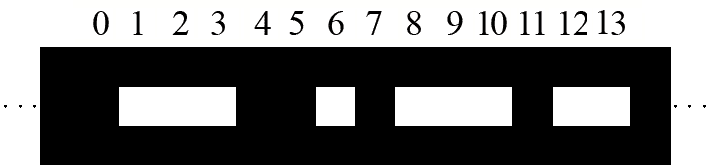
Вася хочет научиться накладывать одну ленту на другую таким образом, чтобы на просвет образовывалось как можно больше дырочек. Кроме этого, требуется, чтобы приведенную ленту можно было вставить в декодирующее устройство, т.е. длина каждого просвета и расстояние между любыми просветами выражались бы целым числом сантиметров, а края лент были совмещены. Поворачивать и переворачивать ленты запрещается. Напишите про грамму, которая по заданным сообщениям определяла бы, какое максимальное количество дырочек можно получить.
Формат входного файла
Входной файл состоит из двух строк: в первой строке задается сообщение, записанное на первой ленте, на второй – записанное на второй. Сообщения непусты, и состоят не более, чем из 130 000 битов.
Формат выходного файла
В выходной файл выведите максимально возможное количество дырочек.
Пример
|
holytape.in |
holytape.out |
|
01110010111011 1001001001 |
4 |
|
11111111111000000000110000000 00001100000000000000001111111 |
2 |
В первом примере можно, например, сдвинуть вторую ленту вправо на 3 сантиметра относительно первой. Во втором примере одним из возможных оптимальных сдвигов является сдвиг влево на 2 см.
Летние учебно-тренировочные сборы, Петрозаводск, 30 августа 2006 года
Задача H. ДНК роботов
Имя входного файла
robots.in
Имя выходного файла
robots.out
Ограничение по времени
2 секундs
Ограничение по памяти
64 мегабайта
Используя недавно открытые методы искусственного конструирования ДНК, ученые НИИ Данных Строк (НИИ ДС) начали величайший эксперимент по строительству биологических роботов.
Для упрощения необходимого программного обеспечения было принято решение использовать ДНК из M = 2n (2 ≤ n)символов. Более того, по техническим причинам в ДНК роботов использованы не обычные строки, а циклические, поэтому их можно читать с любого места.
Среди вопросов, которые планируется исследовать в ходе эксперимента, особый интерес представляет анализ мутаций роботов. После длительного периода наблюдений были обнаружены несколько типов роботов. При попытке восстановить дерево мутаций ученые НИИ ДС столкнулись со следующей задачей: им необходима программа для вычисления коэффициента совпадения ДНК двух роботов. Коэффициент совпадения двух ДНК – это количество букв, которые в них совпадут, если циклически сдвинуть вторую ДНК относительно первой наиболее удачным образом, то есть так, чтобы число совпадающих букв было как можно больше.
Вам нужно написать программу, вычисляющую коэффициент совпадения.
Формат входного файла
В первой строке входного файла записано одно число M (4 ≤ М ≤ 131 072). Следующие две строки содержат ДНК, которые необходимо исследовать. Обе эти строки содержат ровно М символов, каждый из которых – это одна из следующих латинских букв: 'A', 'C', 'G' или 'T' (они обозначают аденин, цитозин, гуанин или тимин, соответственно).
Пример
|
robots.in |
robots.out |
|
16 ACGTACGTACGTACGT CGTACGTACGTACGTC |
15 1 |
Литература
Г. И. Архипов. Лекции по математическому анализу: Учеб. для вузов / Г. И. Архипов, В. А. Садовничий, В. Н. Чубариков; Под ред. В. А. Садовничего – 3-е изд., перераб. и доп. - М.: Дрофа, 2003 – 640 с. – (Высшее образование: современный учебник). Глава 5, Лекция 27, Теорема 34 (стр. 152-153)
Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клиффорд. Алгоритмы: построение и анализ, 2-е издание. : Пер. с англ. – М. : Издательский дом «Вильямс», 2005. – 1276 с. : ил. – Парал. тит. англ. Часть 7, Глава 30 (стр. 926 – 953)
Daniel N. Rockmore, "The FFT — an algorithm the whole family can use", Comput. Sci. Eng. 2 (1), 60 (2000). Special issue on "top ten" algorithms of the century. (http://www.cs.dartmouth.edu/~Erockmore/cse-fft.pdf)