Теоретический материал
| Сайт: | Информатикс |
| Курс: | Алгоритмы на строках |
| Книга: | Теоретический материал |
| Напечатано:: | Гость |
| Дата: | Пятница, 27 Июнь 2025, 13:59 |
А. Климовский
Рассмотрим следующую простую задачу: реализовать множество строк (операции добавление, удаление и поиск). С этой задачей успешно справляется структура данных бор. Вместо того чтобы давать строгое определение, лучше рассмотрим, как он работает.
З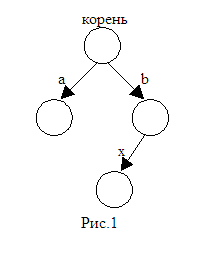
аведем
корневое дерево, у которого на каждом
ребре написан символ алфавита. Из каждой
вершины дерева существует ребро к
потомкам, если и только если в том
поддереве есть элементы. Каждая вершина
соответствует строке, получающейся на
пути от корня до этой вершины. Например,
вершинам на рис. 1 соответствуют строки
“”, “a”, “b”,
“bx” (пустая строка
соответствует корню). Это только строки,
которые соответствуют вершинам, а не
элементы реализуемого множества.
Реализуемым множеством будет часть этих строк. Для того чтобы хранить, какие именно строки входят в множество, а какие — нет, прикрепим к каждой вершине дерева флаг. Его истинность и будет означать, есть ли соответствующая строка в множестве.
Иногда бывает удобно по-другому маркировать элементы множества: заканчивать строки некоторым терминальным символом (например “$”). Здесь мы так делать не будем.
Приступим к реализации.
type
PEl = ^TEl;
TEl = record // Тип для вершины
f : boolean;
Link : array ['a' .. 'z'] of PEl;
end;
В олимпиадном программировании не рекомендуется использовать динамические переменные, так как операция new довольно долго выполняется. Поэтому заведем массив и счетчик использованных элементов.
При желании можно модифицировать реализацию с использованием динамических переменных и, таким образом, освобождать память после удаления строки. Для эффективной реализации вышеизложенного можно завести в каждой вершине счетчик количества элементов множества в поддереве, но в олимпиадах это практически не используется, поэтому останавливаться на этих модификациях не будем.
var
bor : array [0 .. maxEl] of TEl;
uk : integer; root : PEl;
procedure Init;
begin
fillchar(bor, sizeof(bor), 0);
uk := 0; root := @bor[0];
end;
procedure Insert(const s : string);
var
cur : PEl;
i : integer;
begin
cur := root;
for i := 1 to length(s) do begin
if cur^.Link[s[i]] = nil then begin
inc(uk);
cur^.Link[s[i]] := @bor[uk];
end;
cur := cur^.Link[s[i]];
end;
cur^.f := true;
end;
procedure Delete(const s : string);
var
cur : PEl;
i : integer;
begin
cur := root;
for i := 1 to length(s) do begin
if cur^.Link[s[i]] = nil then begin
Writeln('No such string');
exit;
end;
cur := cur^.Link[s[i]];
end;
cur^.f := false;
end;
function Search(const s : string) : boolean;
var
cur : PEl;
i : integer;
begin
cur := root;
for i := 1 to length(s) do begin
if cur^.Link[s[i]] = nil then begin
result := false;
exit;
end;
cur := cur^.Link[s[i]];
end;
result := cur^.f;
end;
Оценим сложность операций над этой структурой данных. Все операции (добавление, удаление, поиск) для данной строки длины L выполняются за время O(L), при этом памяти требуется O(S*M), где S — сумма длин всех строк, M — размер алфавита. Видно, что узкое место структуры данных в объеме используемой памяти.
Рассмотрим метод устранения этого недостатка.
Рассмотрим метод уменьшения объема используемой памяти. Модифицированная структура называется сжатым бором. Дополнительная идея состоит в том, что на ребрах дерева можно записывать не один символ, а сразу все символы до очередного ветвления дерева. Таким образом, необходимо заменить записываемый на ребре символ на строку и одновременно с этим запретить ситуацию, когда на двух ребрах, исходящих из одной вершины, написаны строки с одинаковыми первыми символами (в таком случае структура должна содержать одно общее ребро, ведущее в дополнительную вершину, соответствующую концу совпадающего префикса). Тогда индексировать ребра можно по первому символу, но при выполнении операций, разумеется, сверять всю написанную подстроку (на случай, если искомой строки нет).
Рассмотрим теперь реализацию сжатого бора на примере задачи номер 2 «Файловый менеджер» с Всероссийской олимпиады 2006.
Решение состоит из нескольких частей (построение графа, поиск в нем пути и других), мы же только рассмотрим построение всех переходов по кнопке Alt (основная часть построения графа).
Далее для краткости изложения отождествим вершину бора и строку, ей соответствующую. Также будем понимать под циклической последовательностью следующую: 1, 2, …, N, 1, 2, …, N, 1, 2, …
Опишем решение задачи, пока не затрагивая реализацию. Пусть курсор находится на файле с номером k. Тогда переход по кнопке Alt и строке s — это ближайший после k-ого в циклической последовательности файл, имеющий строку s в качестве префикса своего имени. Для того чтобы рассмотреть все кратчайшие переходы, очевидно, достаточно в качестве строк s рассмотреть только строки, являющиеся префиксом имени хотя бы одного файла.
Попробуем использовать бор для реализации этого решения задачи. Сначала рассмотрим частный случай: построим переходы из первого файла. Еще раз поймем, какую функциональность мы хотим от модифицированного бора. Необходимо для каждой строки s знать номер первого файла, имеющего эту строку s в качестве префикса своего имени (это и будет тот файл, на который мы перейдем, нажав Alt и s). Поэтому, можно в каждой вершине бора завести поле first и добавлять все файлы (их имена) в порядке с первого по последний и при создании вершины в это поле записывать номер файла, который в тот момент добавлялся. (Так как при добавлении строки мы пройдем ровно те вершины, которым соответствуют префиксы этой строки.) Тогда, обойдя дерево (например, обходом в глубину), можно просмотреть все префиксы всех файлов и для каждого из них получить переход из первого файла в тот, который записан в поле first вершины этого префикса.
Но есть недостаток этой реализации: для каждой вершины строить заново бор слишком долго. Поэтому реализуем этот частный случай чуть по-другому (далее станет понятно, зачем). Будем идти по файлам в обратном порядке (с последнего по первый) и переписывать поле first каждый раз, когда проходим по вершине (при этом мы пройдем все префиксы имени файла). Несложно понять, что мы опять получили то же самое необходимое заполнение полей first.
Теперь посмотрим, что нужно сделать, чтобы перейти от построения переходов из первого файла к построению переходов из последнего. Для этого нужно было бы добавить файлы n–1, n–2, …, 2, 1, n. Но сравнивая это с тем, что у нас уже есть, получаем, что нужно просто еще раз добавить n-ый файл. И так далее…
Ниже приведен код разобранной части решения задачи.
type
TEl=record
First : int; // Номер строки, описанной выше
i, j : int; // Границы подстроки, написанной на ребре
link : array ['a'..'z'] of int; // Ссылки на «детей»
end;
var
bor : array [0..max] of TEl;
uk : int;
//Добавление строки j
procedure Add(j: int);
var cur, t, x : int;
begin
cur := 0; t := 1;
while t <= length(a[j]) do begin
if bor[cur].link[a[j][t]] = 0 then begin
//Добавление новой вершины
inc(uk);
fillchar(bor[uk], sizeof(bor[uk]), 0);
bor[cur].link[a[j][t]] := uk;
bor[cur].first := j;
bor[uk].first := j;
bor[uk].i := t;
bor[uk].j := length(a[j]);
Break;
End
else begin
//Переход по существующему ребру
bor[cur].first := j;
cur := bor[cur].link[a[j][t]];
x:=bor[cur].i;
//Подсчет количества совпадающих символов на ребре
while (x <= bor[cur].j) and (x <= length(a[j])) and
(a[j][x] = a[bor[cur].first][x]) do inc(x);
dec(x);
if x <> bor[cur].j then begin
//Ребро нужно делить
//Старая вершина отходит продолжению старой ветви
//Создание вершины деления
inc(uk);
fillchar(bor[uk], sizeof(bor[uk]), 0);
bor[uk].first := bor[cur].first;
bor[uk].i := x + 1;
bor[uk].j := bor[cur].j;
bor[uk].link := bor[cur].link;
bor[cur].first := j;
bor[cur].j := x;
fillchar(bor[cur].link, sizeof(bor[cur].link), 0);
bor[cur].link[a[bor[uk].first][x+1]] := uk;
if x <> length(a[j]) then begin
//Создание вершины для новой строки
inc(uk);
fillchar(bor[uk], sizeof(bor[uk]), 0);
bor[uk].first := j;
bor[uk].i := x + 1;
bor[uk].j := length(a[j]);
bor[cur].link[a[bor[uk].first][x+1]] := uk;
end;
Break;
end
else begin //Ребро не нужно делить
t := x + 1;
bor[cur].first := j;
end;
end;
end;
end;
//Поиск всех путей по Alt из from в поддереве cur
procedure Dfs(from, cur : int);
var lp : char;
begin
if cur <> 0 then begin
//Попытка добавить путь из from в текущую вершину
if g[from,bor[cur].first] > bor[cur].i + 1 then
g[from,bor[cur].first] := bor[cur].i + 1;
end;
for lp := 'a' to 'z' do
if bor[cur].link[lp] <> 0 then dfs(from, bor[cur].link[lp]);
end;
Begin
uk := 0; fillchar(bor[0], sizeof(bor[0]), 0); bor[0].j := -1;
// Инициализация бора
for j := N downto 1 do Add(j); // Добавляем слова
for i := N downto 1 do begin
Add(i); Dfs(i,0); // Обновляем данные и ищем все искомые пути из вершины
end;
End.
Оценим теперь память. Так как в каждой вершине что-то ответвляется или заканчивается строка, несложно доказать, что количество вершин O(N). Итого памяти O(N*M), где M — опять же длина алфавита. В большинстве задач это вполне приемлемо.
Можно отметить, что бор подходит не только для множеств, но и для хранения для каждой строки каких-либо данных (для этого нужно просто заменить тип f на указатель на эти данные). Кроме строк могут быть многие составные объекты.
В отдельном материале можно найти применение бора в решении задачи методом динамического программирования по профилю.
Литература
[1] Дэн Гасфилд. «Строки, деревья и последовательности в алгоритмах. Информатика и вычислительная биология»
[2] Кормен, Лейзерсон, Ривест. «Алгоритмы: построение и анализ»
program bor1;
{$APPTYPE CONSOLE}
uses
SysUtils;
const
maxEl=1000;
type
PEl = ^TEl;
TEl = record
f : boolean; // Имеется ли в множестве данная строка
Link : array ['a' .. 'z'] of PEl; // Указатели на "детей"
end;
var
bor : array [0 .. maxEl] of TEl;
uk : integer;
root : PEl;
procedure Init;
begin
fillchar(bor, sizeof(bor), 0);
uk := 0;
root := @bor[0];
end;
procedure Insert(const s:string);
var
cur : PEl;
i : integer;
begin
cur:=root;
for i := 1 to length(s) do
begin
if cur^.Link[s[i]] = nil then
begin
inc(uk);
cur^.Link[s[i]] := @bor[uk];
end;
cur:=cur^.Link[s[i]];
end;
cur^.f := true;
end;
procedure Delete(const s:string);
var
cur : PEl;
i : integer;
begin
cur:=root;
for i := 1 to length(s) do
begin
if cur^.Link[s[i]] = nil then
begin
Writeln('No such string');
exit;
end;
cur:=cur^.Link[s[i]];
end;
cur^.f := false;
end;
function Search(const s:string) : boolean;
var
cur : PEl;
i : integer;
begin
cur:=root;
for i := 1 to length(s) do
begin
if cur^.Link[s[i]] = nil then
begin
result := false;
exit;
end;
cur:=cur^.Link[s[i]];
end;
result := cur^.f;
end;
begin
Init;
Insert('SFdsdf');
Insert('SFdsdwe');
Insert('SFdew');
Writeln(Search('SFdew'));
Readln;
end.
XVIII Всероссийская олимпиада школьников по информатике
Первый тур, Кисловодск, 23 апреля 2006 года
Задача 2. Файловый менеджер
Общий шаг алгоритма – k раз находить кратчайшие пути из одной вершины в другую на предварительно построенном графе.
Будем называть имена файлов строками.
Рассмотрим полный ориентированный граф с N вершинами, где вершина i соответствует файлу номер i. Вес ребра (i, j) – минимальная стоимость добраться из позиции курсора номер i в позицию j, используя только одну возможность менеджера (нажать клавишу вверх, нажать клавишу вниз, нажать клавишу Alt и последовательность символов). Ребра, реализующие первые две возможности (up, down), соединяют все вершины, номера которых отличаются на 1. Вес таких ребер равен 1.
Самая главная сложность этой задачи состоит в том, чтобы быстро найти веса ребер для последней возможности (Alt + <Text>). Вес такого ребра (i, j) – минимальная длина последовательности нажатий клавиш, которая переводит курсор с i-го файла на j-й. Если из i в j нельзя попасть только с помощью “Alt”, то вес ребра будет плюс бесконечность.
Таким образом, чтобы найти последовательность нажатий минимальной длины, перемещающую курсор из позиции A в позицию B, надо найти кратчайший путь из A в B в нашем графе.
Если запустить алгоритм Дейкстры из вершины A, то в d[B] получим искомую длину.
Пусть мы знаем, как быстро вычислять массив common[i][j] = максимальный общий префикс строк номер i и j. Тогда d[i][j] – вес ребра (i, j) – равен максимуму среди (common[t][j] + 2) i <=t < j (если i > j, то t пробегает значения i, i + 1, …N, 1, …, j – 1). Это верно, так как надо нажать сначала Alt, потом max(common[t][j]) букв, потом еще одну. Если нажать менее чем d[i][j] клавиш, то курсор попадет на какую-нибудь строку между i и j. Если d[i][j] получилось больше, чем длина j-го слова + 1, то из i в j нельзя попасть только с помощью “Alt”, d[i][j] присваиваем плюс бесконечность.
Например, для набора
aaa
baa
aa
bbbb
bbcc
d[1][5] = 4, d[1][3] = +∞.
Вычисление D по common несложно реализовать за O(N2) следующим образом:
d[j – 1][j] = common[j – 1][j] + 2,
d[j – 2][j] = max(common[j – 2][j] + 2, d[j – 1][j]),
…
d[i][j] = max(common[i][j] + 2, d[i + 1][j]).
Обсудим три способа найти common[i][j] для всех i, j.
а) O(N*log(N)*L), где L – максимальная длина слов.
Отсортируем все имена в лексикографическом порядке, пусть строка i имеет номер P(i) в отсортированном списке.
Найдем c[P(i)] – размер наибольшего общего префикса строк P(i), P(i + 1). Тогда common[i][j], где
P(i) < P(j) – минимум среди всех c[t], P(i) ≤ t < P(j). Действительно, если P(i) и P(j) имеют общий префикс длиной L, то c[t] ≥ L, причем должно быть хотя бы одно равенство.
Тогда
common[P(j – 1)][P(j)] = c[P(j – 1)],
common[P(j – 2)][P(j)] = max(c[j – 2], common[P(j – 1)][P(j)]),
…
common[P(i)][P(j)] = max(c[P(i)], common[P(i + 1)][P(j)]).
б) O(N2 + N*L) (предложено одним из участников)
Будем искать common методом динамического программирования.
Пусть B[i + 1][j] – такое 1 ≤t ≤ j, что common[i + 1][t] максимально.
Допустим, вычислены все common[a][b] и B[a][b], a ≤ i, b ≤ i. Научимся находить common[i + 1][j + 1] и
B[i + 1][j + 1] при условии, что для всех пар (i + 1, t), t ≤ j, все уже вычислено. Возьмем A = B[i + 1][j]. Тогда первые min(common[i + 1][A], common[A][j + 1]) символов у строк (i + 1) и (j + 1) совпадают. Тогда если
common[j + 1][A] < common[i + 1][A], то
common[i + 1][j + 1] = common[j + 1][A] и
B[i + 1][j + 1] = A.
В противном случае находим common[i + 1][j + 1] непосредственно сравнивая символы с номерами common[i + 1][A] + 1, …, L у строк (i + 1), (j + 1), пока не найдется несовпадения. При этом
B[i + 1][j + 1] = max(common[i + 1][j + 1], B[i + 1][j]).
Таким образом, для каждого (i + 1) непосредственных сравнений будет не более L, остальных действий O(N), так что заявленная оценка верна.
в) O(S + N2), где S – суммарная длина всех имен файлов.
Допишем к концу каждого имени файла символ “$”. Построим сжатый бор из таких расширенных строк (подробнее о борах см. [1]). Тогда каждой строке будет соответствовать лист в боре (у которого путевая метка равна расширенной строке). В противном случае получим, что префиксом какой-то строки A будет S$, где S – строка без листа, тогда A = S, чего не может быть по условию.
Тогда common[i][j] - длина путевой метки наименьшего общего предка для пары листьев, соответствующих строкам i, j (обозначается LCA(i, j)).
Вспомним, как алгоритм поиска в глубину раскрашивает вершины в процессе работы: вначале все вершины белые; когда вершина только начинает обрабатываться, ее красят в серый цвет; после того, как все ее сыновья (или вершины, в которые из нее ведут ребра) станут черными (обработанными), она становится черной.
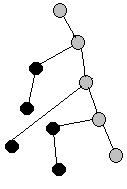
Предложение. Пусть вершину j только что перекрасили в серый цвет (это значит, что все ее сыновья еще белые). Тогда LCA(i, j) для любой черной i будет q(i) - наиболее удаленная от корня серая вершиной, являющейся предком i.
Так как конфигурация серых и черных вершин меняется по ходу выполнения алгоритма, то будем различать q(i) для разных моментов времени (в частности, когда i не является черной, q(i) не определена).
Итак, будем обходить в глубину из корня наш бор как дерево. В массиве q[i] в любой момент времени будет храниться q(A) в текущий момент времени, где A – лист, соответствующий строке i. Также будет храниться список листьев, уже ставших черными. Тогда при перекрашивании очередного листа в серый цвет надо пробежаться по списку уже черных и проставить соответствующие значения common. При перекрашивании листа в черный цвет надо добавить его в список черных. Если при обработке любой вершины u оказывается, что q[i] для какого-то i ссылается на черную вершину, то q[i] – значение q(A) для предыдущего момента времени, и q[i] надо изменить на u.
Подробнее об алгоритме поиска LCA см. [2] среди задач к разделу «Обход в глубину».
Литература.
[1]. Дэн Гасфилд. «Строки, деревья и последовательности в алгоритмах. Информатика и вычислительная биология»
[2]. Кормен, Лейзерсон, Ривест. «Алгоритмы: построение и анализ»
{$A8,B-,C+,D-,E-,F-,G+,H+,I-,J-,K-,L-,M-,N+,O+,P+,Q-,R-,S-,T-,U-,V+,W-,X+,Y+,Z1}
//{$A8,B-,C+,D+,E-,F-,G+,H+,I+,J-,K-,L+,M-,N+,O-,P+,Q+,R+,S+,T-,U-,V+,W-,X+,Y+,Z1}
{$MAXSTACKSIZE 30000000}
program Fur;
{$APPTYPE CONSOLE}
uses
SysUtils;
type
int=longint;
real=extended;
bool=boolean;
TEl=record
first:int;
i,j:int;
link:array['a'..'z']of int;
end;
const
in_f='fur.in';
out_f='fur.out';
maxN=1000+5;
maxL=2000+5;
maxK=10+5;
max=2*maxN;
var
N:int;
a:array[1..maxN] of string;
k:int;
need:array[1..maxK] of int;
g:array[1..maxN,1..maxN] of int;
way:array[1..maxN,1..maxN] of string[2];
inf:int;
bor:array[0..max] of TEl;
uk:int;
d,link:array[1..maxN] of int;
ok:array[1..maxN] of bool;
procedure WriteAns(aa,bb:int);
var
i,min:int;
procedure WriteS(i,j:int);
var
t:int;
begin
if way[i,j][1]='!' then
begin
if way[i,j][2]='u' then
Writeln('up')
else
Writeln('down');
end
else
begin
Writeln('Alt');
for t := 1 to g[i,j]-1 do
Writeln(a[j][t]);
end;
end;
procedure WriteIt(i:int);
begin
if link[i]<>0 then
begin
WriteIt(link[i]);
WriteS(link[i],i);
end;
end;
begin
for i:= 1 to N do
d[i]:=inf;
fillchar(ok,sizeof(ok),0);
fillchar(link,sizeof(link),0);
d[aa]:=0;
min:=aa;
while min<>bb do
begin
for i := 1 to N do
if d[i]>g[min,i]+d[min] then
begin
d[i]:=g[min,i]+d[min];
link[i]:=min;
end;
ok[min]:=true;
for i:= 1 to N Do
if not ok[i] then
min:=i;
for i:= 1 to N do
if not ok[i] and (d[i]<d[min]) then
min:=i;
end;
Writeln(d[bb]);
WriteIt(bb);
end;
procedure Add(j:int);
var
cur,t,x:int;
begin
cur:=0;
t:=1;
while t<=length(a[j]) do
begin
if bor[cur].link[a[j][t]]=0 then
begin
inc(uk);
fillchar(bor[uk],sizeof(bor[uk]),0);
bor[cur].link[a[j][t]]:=uk;
bor[cur].first:=j;
bor[uk].first:=j;
bor[uk].i:=t;
bor[uk].j:=length(a[j]);
BReak;
end
else
begin
bor[cur].first:=j;
cur:=bor[cur].link[a[j][t]];
x:=bor[cur].i;
while (x<=bor[cur].j) and (x<=length(a[j])) and (a[j][x]=a[bor[cur].first][x]) do
inc(x);
dec(x);
if x<>bor[cur].j then
begin
inc(uk);
fillchar(bor[uk],sizeof(bor[uk]),0);
bor[uk].first:=bor[cur].first;
bor[uk].i:=x+1;
bor[uk].j:=bor[cur].j;
bor[uk].link:=bor[cur].link;
bor[cur].first:=j;
bor[cur].j:=x;
fillchar(bor[cur].link,sizeof(bor[cur].link),0);
bor[cur].link[a[bor[uk].first][x+1]]:=uk;
if x<>length(a[j]) then
begin
inc(uk);
fillchar(bor[uk],sizeof(bor[uk]),0);
bor[uk].first:=j;
bor[uk].i:=x+1;
bor[uk].j:=length(a[j]);
bor[cur].link[a[bor[uk].first][x+1]]:=uk;
end;
Break;
end
else
begin
t:=x+1;
bor[cur].first:=j;
end;
end;
end;
end;
procedure Run;
var
i,j,cur:int;
procedure Dfs(cur:int);
var
lp:char;
begin
if cur<>0 then
begin
if g[i,bor[cur].first]>bor[cur].i+1 then
begin
g[i,bor[cur].first]:=bor[cur].i+1;
way[i,bor[cur].first]:='-';
end;
end;
for lp:= 'a' to 'z' do
if bor[cur].link[lp]<>0 then
dfs(bor[cur].link[lp]{,ans});
end;
begin
Readln(n);
for i:= 1 to N do
readln(a[i]);
Read(K);
for i := 1 to K do
Read(need[i]);
inf:=N+10;
for i:= 1 to N do
for j := 1 to N do
g[i,j]:=inf;
for i := 1 to N do
begin
g[i,i mod N+1]:=1;
way[i,i mod N+1]:='!d';
g[i mod N+1,i]:=1;
way[i mod N+1,i]:='!u';
end;
for i:= 1 to N do
begin
g[i,i]:=0;
way[i,i]:='';
end;
uk:=0;
fillchar(bor[0],sizeof(bor[0]),0);
bor[0].j:=-1;
for j := N downto 1 do
Add(j);
for i := N downto 1 do
begin
Add(i);
Dfs(0{,''});
end;
{
for i:= 1 to N Do
begin
for j := 1 to N do
Write(g[i,j],' ',way[i,j], ' ');
Writeln;
end;
}
cur:=1;
for i := 1 to k do
begin
WriteAns(cur,need[i]);
cur:=need[i];
end;
end;
procedure OpenFiles;
begin
Reset(input,in_f);
Rewrite(output,out_f);
end;
procedure CloseFiles;
begin
Close(input);
Close(output);
end;
begin
OPenFiles;
Run;
CLoseFiles;
end.