Теоретический материал
| Сайт: | Информатикс |
| Курс: | Структуры данных |
| Книга: | Теоретический материал |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 15 Февраль 2026, 03:57 |
На практике часто возникают задачи, в которых приходится работать с динамически изменяющимися данными. Дерево Фенвика является структурой данных, позволяющей достаточно эффективно выдавать ответы на запросы о частичных суммах на различных отрезках массива, элементы которого могут меняться в процессе работы.
Пусть задан массив A из N чисел: A0, A1, ..., AN - 1. Дерево Фенвика -- это структура данных, позволяющая выполнять две операции:
- rsq(i, j) -- выдать сумму элементов массива A с i-го по j-й включительно (rsq является сокращением от range sum query);
- update(k, d ) -- прибавить к k-му элементу массива A некоторое число d.
При простейшей реализации rsq(i, j) работает за время O(j - i + 1), что в общем случае составляет порядка O(N), а update(k, d ) -- за O(1). Для ответа на запрос rsq(i, j) достаточно в цикле просуммировать указанный отрезок массива, а при выполнении операции update(k, d ) -- изменить k-й элемент Ak.
Заметим однако, что при большом количестве запросов вида rsq(i, j) простейшая реализация не слишком эффективна, так как в общем случае ответ на каждый запрос требует времени, зависящего линейно от длины массива.
Дерево Фенвика позволяет существенно сократить это время, поскольку выполняет каждую из указанных операций за время O(log N).
Описание структуры
На практике дерево Фенвика представляет собой массив B из N чисел: B0, B1, ..., BN - 1, в k-м элементе которого хранится сумма элементов массива A с f (k)-го по k-й: Bk = ![]() Ai, где f (k) = k& (k + 1). Под & имеется ввиду операция побитового И.
Ai, где f (k) = k& (k + 1). Под & имеется ввиду операция побитового И.
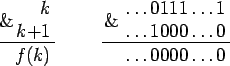
Рис. 1.
Рассмотрим двоичное представление числа k (рис. 1): пусть в нем сначала идет произвольная последовательность 0 и 1, потом 0 и дальше некоторое количество единиц, в том числе нулевое. f (k) получается из k заменой всех этих подряд идущих единиц в младших разрядах нулями. Если же в младшем разряде числа k стоит 0, то f (k) = k. Так, например, для k = 1110 = 10112 получаем f (k) = 10002 = 810, а для k = 1010 = 10102 получаем f (k) = 10102 = 1010. Отметим важное свойство функции f: 0![]() f (k)
f (k)![]() k для любого k
k для любого k![]() 0.
0.
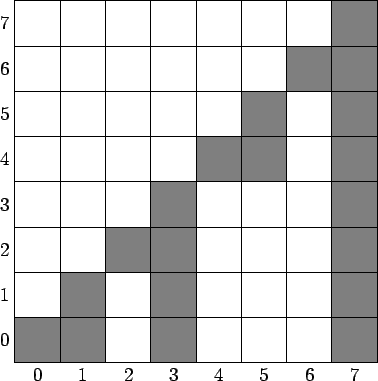
Рис. 2.
Диаграмма на рис. 2 показывает, что будет храниться в массиве B (дереве Фенвика) при N = 8: клетка i-й строки k-го столбца заштрихована, если Ai входит в частичную сумму Bk, то есть f (k)![]() i
i![]() k.
k.
Рассмотрим, как с помощью дерева Фенвика реализуются операции ответа на запрос rsq(i, j) о частичной сумме элементов массива A с i-го по j-й и запрос update(k, d ) прибавления к k-му элементу массива A числа d.
Ответ на запрос о частичной сумме элементов массива A -- rsq(i, j)
Заметим, что rsq(i, j) = rsq(0, j) - rsq(0, i - 1) (для i = 0 положим rsq(0, - 1) = 0). Таким образом, для ответа на запрос rsq(i, j) достаточно научиться отвечать на запрос вида rsq(0, k), который для краткости обозначим rsq(k).
Ответ на запрос rsq(k) вычисляется следующим образом:
Перепишем эту формулу в видеПокажем, почему указанная сумма ([*]) действительно будет являться ответом на запрос rsq(k), то есть Bk0 + Bk1 + Bk2 +...+ Bkn = ![]() Ai.
Ai.
Действительно,
=
 Ai =
Ai = =
 Ai +
Ai + 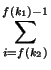 Ai +...+
Ai +...+ 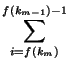 Ai =
Ai = =
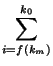 Ai.
Ai. Для последнего индекса km верно: f (km) - 1 < 0, откуда в силу неотрицательности f (km) следует f (km) = 0, то есть 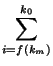 Ai =
Ai = ![]() Ai. Таким образом, указанная сумма ([*]) и будет суммой всех элементов массива A с 0-го по k-й.
Ai. Таким образом, указанная сумма ([*]) и будет суммой всех элементов массива A с 0-го по k-й.
Например, для k = 14 по формуле ([*]) имеем:
=
Ниже приводится текст подпрограммы, реализующий ответ на запрос rsq(k):
1: Function rsq(k : LongInt) : LongInt;
2: var
3: res : LongInt;
4: begin
5: res := 0;
6: while (k >= 0) do begin
7: inc(res, B[k]);
8: k := k and (k + 1) - 1;
9: end;
10: rsq := res;
11: end;
| k0 | 14 | 11102 |
| f (k0) | 14 | 11102 |
| k1 | 13 | 11012 |
| f (k1) | 12 | 11002 |
| k2 | 11 | 10012 |
| f (k2) | 8 | 10002 |
| k3 | 7 | 01112 |
| f (k3) | 0 | 0002 |
Рис. 3.
Для оценки времени работы данной подпрограммы необходимо оценить количество итераций цикла while в строках 6-9, то есть количество слагаемых m в сумме ([*]). Для этого рассмотрим двоичное представление числа k и то, как оно преобразуется при вычислении номера следующего индекса суммы по предыдущему: ki + 1 = f (ki) - 1, где k0 = k.
Сделаем это на примере для k = 14 (рис. 3). Количество слагаемых равно количеству единичных битов в числе f (k) плюс один. Переход к каждому следующему индексу «выбивает» ровно по одному единичному биту из числа f (ki). А поскольку в худшем случае количество единичных бит в f (k) может быть порядка O(log N), то и ответ на запрос rsq(k) в худшем случае требует порядка O(log N) времени.
Изменение k-го элемента массива A -- update(k, d )
При изменении k-го элемента массива A необходимо соответствующим образом изменить элементы массива B, в определении которых частичные суммы содержат элемент Ak. То есть для выполнения операции update(k, d ) (прибавления к k-му элементу массива A числа d) нужно прибавить d к тем элементам Bj массива B, для которых f (j)![]() k
k![]() j.
j.
Утверждается, что все такие j, и только они, являются элементами последовательности k0, k1, k2, ..., km, где k0 = k, ki + 1 = ki | (ki + 1), km + 1 = km | (km + 1) > N - 1. Под | имеется в виду операция побитового ИЛИ.
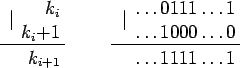
Рис. 4.
Сначала покажем, что указанная последовательность строго возрастает, и ее длина составляет порядка O(log N) в худшем случае. Для этого рассмотрим двоичное представление числа ki (рис. 4). Число ki + 1 получается из ki заменой младшего нулевого бита на единичный. Таким образом, ki + 1 > ki, а длина последовательности m заведомо не превосходит количества бит в двоичном представлении числа N.
| N - 1 | 92 | 10111002 |
| k0 = k | 73 | 10010012 |
| k1 | 75 | 10010112 |
| k2=km | 79 | 10011112 |
| k3 | 95 | 10111112 |
Рис. 5.
На рис. 5 приведен пример указанной последовательности для N = 93 и k = 73.
Покажем, почему элементы последовательности являются индексами тех и только тех элементов массива B, которые нужно изменить при операции update(k, d ).
| j | X0... k |
| k | Y1... k |
Рис. 6.
Поскольку при увеличении номера элемента последовательности, количество единичных битов на конце ki возрастает, то f (ki) убывает. Учитывая еще и то, что сама последовательность ki возрастает, получаем:
Таким образом, все элементы нашей последовательности являются индексами тех элементов массива B, которые надо изменить.
Покажем, что других элементов, которые надо изменить, нет. Предположим, что есть некоторый индекс j, не лежащий в нашей последовательности, такой что f (j)![]() k
k![]() j.
j.
Рассмотрим младший бит, в котором у j стоит 0, а у k стоит 1 -- такой существует, поскольку j не встречается в последовательности ki. Обозначим числа, образованные более старшими битами чисел j и k, через X и Y соответственно. Если X > Y, то j![]() f (j)
f (j)![]() X0...02 > k, а стало быть, частичная сумма Bj не содержит элемента Ak. Если же X
X0...02 > k, а стало быть, частичная сумма Bj не содержит элемента Ak. Если же X![]() Y, то k > j
Y, то k > j![]() f (j) и опять же частичная сумма Bj не содержит элемента Ak. Значит, индексы всех элементов массива B, которые надо изменить присутствуют в последовательности ki.
f (j) и опять же частичная сумма Bj не содержит элемента Ak. Значит, индексы всех элементов массива B, которые надо изменить присутствуют в последовательности ki.
Ниже приводится текст подпрограммы, реализующий операцию изменения update(k, d):
1: Procedure update(k, d : LongInt);
2: begin
3: while (k < N) do begin
4: inc(B[k], d);
5: k := k or (k + 1);
6: end;
7: end;
В силу того, что длина последовательности ki составляет O(log N) в худшем случае, количество итераций цикла while в строках 3-6, а значит, и время работы процедуры update(k, d), составляет O(log N).
Построение дерева Фенвика
Для построения дерева Фенвика по заданному массиву A достаточно изначально взять нулевой массив B из N элементов и N раз вызвать операцию изменения элемента update: update(0, A0), update(1, A1), ..., update(N - 1, AN - 1). Таким образом, построение дерева Фенвика требует O(N log N) времени и O(N) памяти.
Обобщение на двумерный случай
Оказывается, что дерево Фенвика достаточно легко обобщается на двумерный (а вообще говоря, и на k-мерный) случай.
Пусть задан двумерный массив A размера M×N, элементами которого являются числа Aij, 0![]() i
i![]() M - 1, 0
M - 1, 0![]() j
j![]() N - 1. Двумерное дерево Фенвика -- это структура данных, позволяющая выполнять две операции:
N - 1. Двумерное дерево Фенвика -- это структура данных, позволяющая выполнять две операции:
- rsq(x1, y1, x2, y2) -- выдать сумму
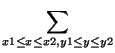 Axy элементов Axy на прямоугольнике x1
Axy элементов Axy на прямоугольнике x1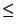 x
x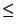 x2, y1
x2, y1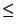 y
y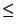 y2;
y2; - update(x, y, d ) -- прибавить к элементу Axy некоторое число d.
Двумерное дерево Фенвика представляет собой двумерный массив B размера M×N, элементами которого являются числа Bxy, 0![]() x
x![]() M - 1, 0
M - 1, 0![]() y
y![]() N - 1. Bxy =
N - 1. Bxy = 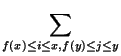 Aij.
Aij.
По аналогии с одномерным случаем заметим (рис. 7), что
- rsq(0, 0, x2, y1-1) + rsq(0, 0, x1-1, y1-1).
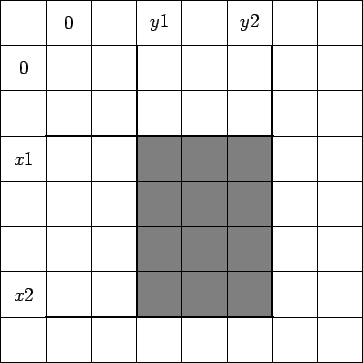
Рис. 7.
Таким образом, для ответа на запрос rsq(x1, y1, x2, y2) достаточно научиться отвечать на запросы вида rsq(0, 0, x, y), которые для краткости обозначим rsq(x, y).
В остальном, реализация операций rsq(x, y) и update(x, y, d ) делается аналогично одномерному случаю из соображений независимости по каждому направлению.
Ниже приводится текст подпрограмм, реализующих операции rsq(x, y) и update(x, y, d ):
1: Function rsq(x, y : LongInt) : LongInt;
2: var
3: i,res : LongInt;
4: begin
5: res := 0;
6: while (x >= 0) do begin
7: i := y;
8: while (i >= 0) do begin
9: inc(res, B[x, i]);
10: i := i and (i + 1) - 1;
11: end;
12: x := x and (x + 1) - 1;
13: end;
14: rsq := res;
15: end;
1: Procedure update(x, y, d : LongInt);
2: var
3: i : LongInt;
4: begin
5: while (x < M) do begin
6: i := y;
7: while (i < N) do begin
8: inc(B[x, i], d);
9: i := i or (i + 1);
10: end;
11: x := x or (x + 1);
12: end;
13: end;
По соображениям, аналогичным тем, что приводились в одномерном случае, времена работы rsq(x, y) и update(x, y, d ) составляют O((log M)(log N)) и O((log M)(log N)) соответственно.
Для построения двумерного дерева Фенвика достаточно взять изначально нулевой массив B и M×N раз применить операцию update: update(x, y, Axy), 0![]() x
x![]() M - 1, 0
M - 1, 0![]() y
y![]() N - 1. Построение двумерного дерева Фенвика требует O(MN(log M)(log N)) времени и O(MN) памяти.
N - 1. Построение двумерного дерева Фенвика требует O(MN(log M)(log N)) времени и O(MN) памяти.
Пример использования
Разберем такую задачу.
Папа Карло нашел длинную палку в сарае и решил сделать из нее вешалку для ключей. Для этого он по всей длине забивает в палку гвоздики в разных местах. Папа Карло время от времени считает, сколько он уже забил гвоздиков на разных участках палки.
Каждое действие Папы Карло -- это либо забивание очередного гвоздика в точке с заданной координатой X, либо подсчет числа забитых гвоздиков на отрезке [X, Y]. Все координаты неотрицательные и не превосходят 109, количество действий не превосходит 105.
Буратино, узнав, в чем дело, решил помочь Папе Карло. Буратино подробно записал все действия Папы Карло в процессе изготовления вешалки и теперь хочет проверить расчеты по числу гвоздиков на разных интервалах, сделанные во время работы. Помогите ему в этом.
Требуется выдать результаты всех расчетов по числу гвоздиков на разных интервалах.
Решение. Если для каждой координаты хранить количество забитых в точку с этой координатой гвоздиков, то подсчет числа гвоздиков на отрезке [X, Y] является запросом rsq(X, Y) к соответствующему дереву Фенвика.
Однако при ограничениях на координаты до 109 такой подход не проходит ни по требуемой памяти, ни по времени работы.
Решением проблемы в данном случае является так называемый «метод сжатия координат». Суть его состоит в следующем: отсортируем по координате все точки, встречающиеся во входном файле (их количество не превосходит 2 . 105). Тут надо учитывать как точки, в которые забиваются гвоздики, так и концы отрезков, на которых производится подсчет числа гвоздиков.
Перенумеруем точки в соответствии с их позицией в отсортированном массиве. При этом точкам с одинаковыми координатами присвоим одинаковые номера.
После этого, заменив координаты всех точек их номерами, задачу можно решать с помощью дерева Фенвика, как это было предложено вначале, поскольку все номера не превосходят 2 . 105.
Литература
[1] P. M. Fenwick, A new data structure for cumulative frequency tables. Software -- Practice and Experience 24, 3 (1994), 327-336, 1994.