Точки и прямые

Теория

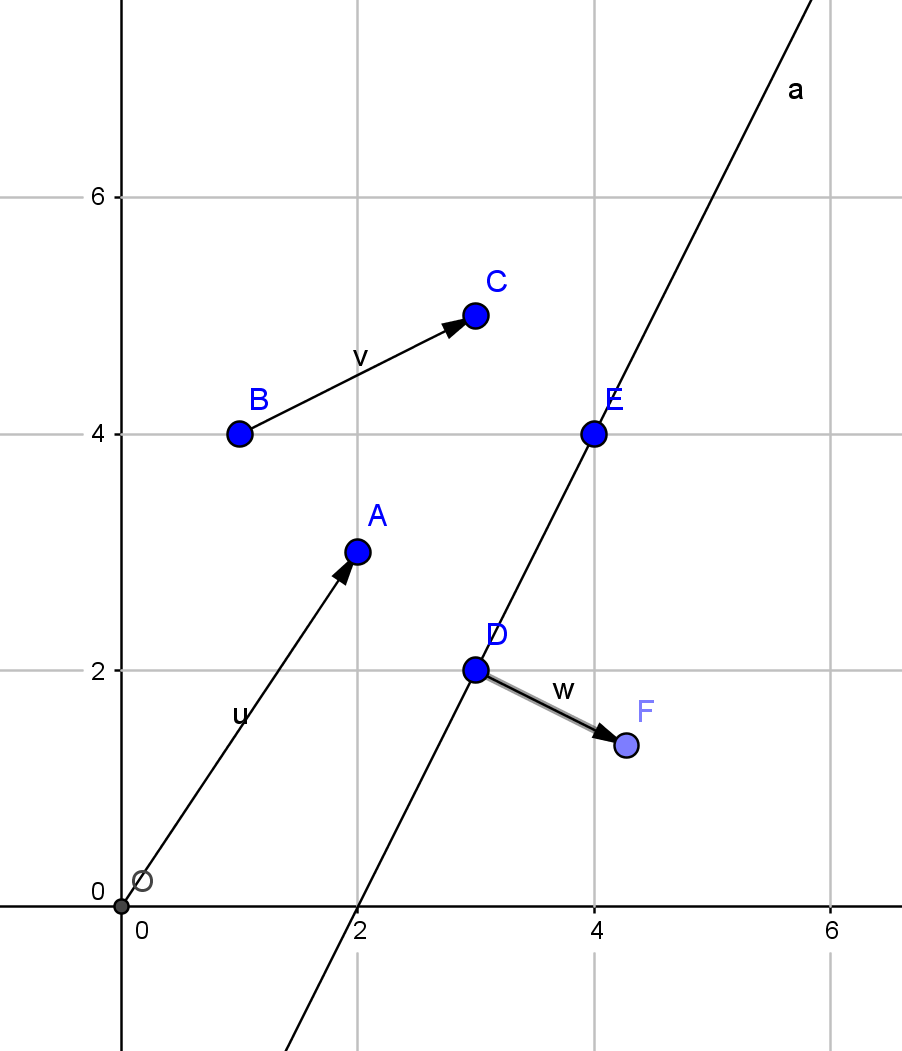Основные понятия:

  • Точка или радиус-вектор – задаются парой координат $A_x, A_y$. Точки будем обозначать большими латинскими буквами($A, B, C...$), векторы - маленькими латинскими буквами из конца алфавита($v, u, w...$).
  • Сумма и разность радиус-векторов определяется как сумма или разность их координат($\vec{u} \pm \vec{v} = {(u_x \pm v_x, u_y \pm v_y)} $). Домножение вектора на число – домножение каждой координаты на число.
  • Вектор – задаётся парой точек $\vec{BC}$, но обычно любой вектор мы будем считать радиус-вектором($C - B$, начало в $0$ координат)
  • Прямая – может задаваться парой точек $\vec{DE}$; точкой и радиус-вектором нормали ($D, w$); уравнением ($Ax + By + C = 0$) Все способы задания эквивалентны и могут быть выражены друг через друга.

1) Например, если прямая задана двумя точками $\vec{DE} = \vec{a}$, тогда радиус вектор нормали к этой прямой будет вектором, перепендикулярным $\vec{DE}$, то есть $(a.y, -a.x)$ или $(-a.y, a.x)$

2) Если прямая задана уравнением $Ax + By + C = 0$, то радиус вектор нормали к этой прямой будет вектором c координатами $(A, B)$ или $(-A, -B)$

Скалярное произведение векторов:

Определяется формулой:

$<\vec{a}, \vec{b}> = a_x*b_x + a_y*b_y = |a| |b| * \cos{a, b}$

|a| - длина вектора, которую можно вычислить следующим образом(по теореме Пифагора)

$|a|^2 = <\vec{a}, \vec{a}>$

Скалярное произведение используется, когда нужно вычислить косинус угла между векторами, либо спроецировать точки в плоскости на прямую.

Скалярное произведение равно нулю, когда векторы коллинеарны. Скалярное произведение больше нуля, когда угол между векторами острый. Скалярное произведение меньше нуля, когда угол между векторами тупой.

Псевдовекторное произведение векторов:

Определяется формулой:

$[\vec{a}, \vec{b}] = a_x*b_y - a_y*b_x = |a| |b| * \sin{a, b}$

Обычно с помощью псевдовекторного произведения определяют с какой стороны от вектора лежит точка.

$[\vec{a}, \vec{b}] = \pm$ площадь параллелограмма с образующими $\vec{a}, \vec{b}$ $=$ $\pm 2 *$ площадь треугольника с образующими $\vec{a}, \vec{b}$

Практика

Для программирования геометрии необходим шаблон, который нужно всегда одинаково писать. Это уменьшает шанс ошибиться и повышает скорость написания программы на олимпиадах.

Например можно для каждого геометрического объекта создавать свой класс, переопределять необходимые операции и дополнять необходимыми методами.

In [11]:
class point(object):
    def __init__(self, x0=0, y0=0):
        self.x = x0
        self.y = y0
    def __add__(self, other):
        return point(self.x + other.x, self.y + other.y)
    #псевдовекторное произведение
    def cross_product(self, A):
        return self.x * A.y - self.y * A.x

Метод _init_ перегружает конструктор класса. Конструктор - создание экземпляра класса. Также можно перегружать арифметические операции и операции сравнения.

In [13]:
A = point(3, 8)
B = point(1, 3)
C = A + B
p = A.cross_product(B)
print('A = ', A.x, A.y)
print('B = ', B.x, B.y)
print('C = ', C.x, C.y)
print('[A * B] = ', p)

A =  3 8
B =  1 3
C =  4 11
[A * B] =  1

продолжение следует