Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).

После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.

ООО «Симптотика» собирается наладить выпуск обучающих игр для детей младшего дошкольного возраста. Одной из придуманных игр был набор кубиков, из которых можно было собирать различные фигуры. Кубики упаковывались в коробку размером N  ×  N  ×  1 кубиков.

Однако, многочисленные маркетинговые исследования показали, что детям неинтересно просто собирать различные фигурки. Гораздо интереснее складывать некоторый набор кубиков на дно коробки в столбики, а после этого переворачивать коробку на 90 градусов по часовой стрелке и смотреть, как именно меняется их расположение. Будем для простоты считать, что коробка поворачивается мгновенно, после чего все кубики падают на дно. На следующем рисунке продемонстрировано, как выглядит расположение кубиков в коробке до и после поворота на 90 градусов.

Разумеется, многим детям становится интересно, как будет выглядеть расположение кубиков после K поворотов в том же направлении. Требуется написать программу, которая вычисляет итоговое положение кубиков в коробке после K поворотов.

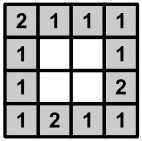
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.

Всем известно, что в 2012 году прошла Летняя Олимпиада в Лондоне, однако не каждый знаком с историей крупнейших спортивных соревнований. Традиция игр зародилась в Древней Греции, но была забыта по завершении античной эпохи и вновь появилась лишь в конце XIX века благодаря французскому общественному деятелю Пьеру де Кубертену.

С 1896 года вновь проводятся летние Олимпийские игры, а с 1924 — зимние, причём оба вида соревнований проходят раз в четыре года. Первое время зимняя и летняя Олимпиады проводились в один и тот же год, но в конце XX века Международный олимпийский комитет принял решение установить между разными видами Игр двухгодичный перерыв. Таким образом, 1992 год был в последний раз отмечен проведением одновременно летних и зимних Олимпийских игр, в 1994 проводились только зимние, в 1996 — летние, и с тех пор они продолжают чередоваться.

Известно также, что в 1916, 1940 и 1944 годах Олимпийские игры были отменены по причине Первой и Второй мировых войн, а в 1906 году проводилась внеочередная Олимпиада.

Требуется написать программу, которая по заданному году определит, проводились ли в этом году Олимпийские игры и были ли они летними или зимними.

Для праздничного чаепития необходимо купить \(n\) пирожных. В магазине продается всего два вида пирожных, причем пирожных одного вида осталось \(a\) штук, а пирожных другого вида осталось \(b\) штук. Пирожные одного вида считаются одинаковыми. Сколькими способами можно купить ровно \(n\) пирожных?