Системы счисления(36 задач)
"Длинная" арифметика(58 задач)
Простые числа и разложение на множители(45 задач)
Остатки(21 задач)
Быстрое возведение в степень(3 задач)
Быстрое преобразование Фурье(3 задач)
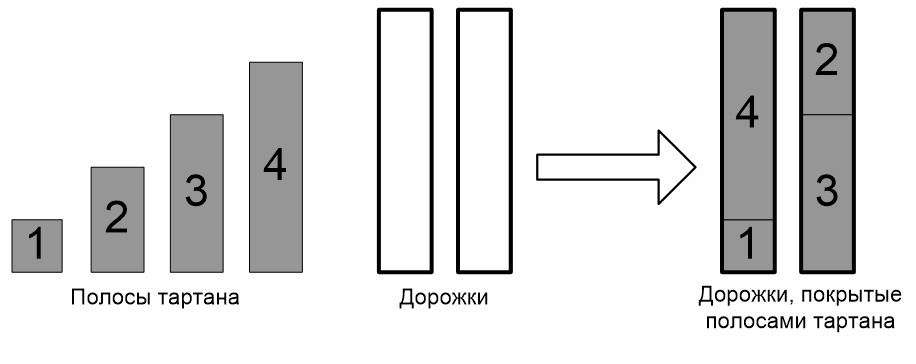
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
В кабинете информатики есть старый стековый калькулятор. Он содержит K ячеек памяти, организованных в виде стека. Первая ячейка называется вершиной стека. На индикаторе калькулятора отображается содержимое вершины стека, если стек непуст.
Над стеком может выполняться операция проталкивания. Применение этой операции приводит к записи числа на вершину стека. Перед этим, если в стеке уже были числа, то каждое из них перемещается в ячейку с номером на единицу больше. Если в стеке уже находится K чисел, то выполнение операции проталкивания невозможно.
Калькулятор позволяет выполнять арифметические операции. Они применяются к числам, хранящимся во второй и первой ячейках стека. Результат операции записывается в первую ячейку стека, а число из второй ячейки удаляется. После этого, если третья ячейка непуста, то число из неё переписывается во вторую, если есть число в четвертой ячейке — оно переписывается в третью и так далее до последней занятой ячейки, которая становится пустой. Для выполнения арифметической операции в стеке должно быть хотя бы два числа. Например, при выполнении операций сложения или умножения, значения соответственно суммы или произведения чисел из первой и второй ячеек помещаются на вершину стека. Операция вычитания выполняется так: из содержимого второй ячейки стека вычитается содержимое первой ячейки.
Известно, что калькулятор неисправен. Из цифровых клавиш работает только клавиша «1». Нажатие этой клавиши приводит к проталкиванию в стек числа 1. Например, попытка набрать число 11, два раза нажав клавишу «1», приводит к тому, что в стек два раза проталкивается число 1. Из операций работают только сложение (клавиша «+»), умножение (клавиша «*») и вычитание (клавиша «-»). Если в результате вычитания получено отрицательное число, то калькулятор зависает.
Легко заметить, что на индикаторе возможно получить произвольное натуральное число. Например, чтобы получить число 3, необходимо дважды нажать клавишу «1», затем клавишу «+» (на индикаторе после этого появится число 2), затем один раз нажать клавишу «1» и один раз — клавишу «+». При K > 2 того же результата можно достичь иначе, трижды нажав клавишу «1», а затем два раза клавишу «+». Дополнительно используя операции умножения и вычитания, в некоторых случаях число N можно получить быстрее, чем сложив N единиц.
Требуется написать программу, которая определяет, каким образом можно получить на индикаторе калькулятора заданное число N, выполнив минимальное количество нажатий клавиш. Стек изначально пуст.
В единственной строке входного файла записаны два натуральных числа — N и K (1 ≤ N ≤ 109, 2 ≤ K ≤ 100).
В первой строке выходного файла выведите минимальное количество нажатий клавиш, необходимых для получения числа N. Если число нажатий не превосходит 200, то дополнительно выведите во второй строке оптимальную последовательность нажатий, приводящих к появлению данного числа на индикаторе.
Последовательность необходимо выводить без пробелов. Клавиши обозначаются символами «1» — протолкнуть число 1 в стек, «+» — выполнить операцию сложения, «*» — выполнить операцию умножения, «-» — вычесть из значения второй ячейки стека значение первой ячейки.
В результате выполнения выведенной последовательности нажатий на индикаторе должно отображаться число N. Если оптимальных последовательностей нажатий несколько, разрешается выводить любую из них.
Примечания
Решения, корректно работающие при N ≤ 100 и K ≤ 10, будут оцениваться из 40 баллов.
Решения, корректно работающие при N ≤ 106 и K ≤ 100, будут оцениваться из 80 баллов.
1 2
1 1
9 3
11 11+1+11+1+*