--->
2 задач
<---
Страница:
1
Отображать по:
#1340
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
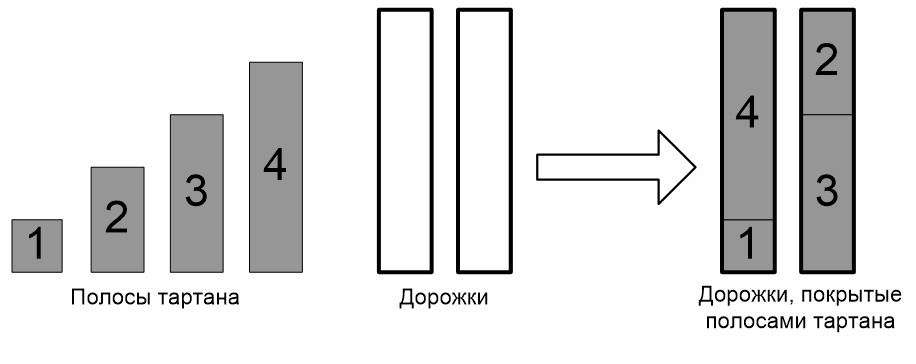
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Входные данные
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
Выходные данные
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
#2530
Темы:
[Перебор с отсечением]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2010,
Задача B
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Задано множество из \(n\) станций и \(m\) трубопроводов, соединяющих некоторые пары станций. Требуется выбрать множество из \(k\) станций, чтобы один из двух концов каждого трубопровода лежал в выбранном множестве. Если построить граф, в котором станции будут служить вершинами, а трубопроводы — рёбрами, то искомое множество будет являться вершинным покрытием в этом графе.
Ханты-Мансийский автономный округ — Югра является важнейшим нефтяным регионом России. Добыча нефти составляет 267 млн т в год, её транспортировка осуществляется по трубопроводам, общая длина которых превышает длину экватора Земли.
Система транспортировки нефти представляет собой совокупность \(n\) распределительных станций и \(m\) трубопроводов. Каждый трубопровод соединяет две различные станции. Между любыми двумя станциями проложено не более одного трубопровода.
Эффективность работы станций существенно зависит от вязкости нефти. Поэтому компания «ЮграНефтеТранс», в ведении которой находится сеть трубопроводов, заказала инновационному исследовательскому предприятию разработку и изготовление новых сверхточных датчиков вязкости на основе самых современных технологий.
Изготовление датчиков — процесс трудоёмкий и дорогостоящий, поэтому было решено изготовить \(k\) датчиков (\(k\le40\)) и выбрать \(k\) различных станций, на которых датчики будут установлены. Необходимо осуществить выбор станций так, чтобы датчики контролировали все трубопроводы: для каждого трубопровода хотя бы один датчик должен быть установлен на станции, где начинается или заканчивается этот трубопровод.
Напишите программу, которая проверяет, существует ли требуемое расположение датчиков, и в случае положительного ответа находит это расположение.
Входные данные
В первой строке входного файла записаны три натуральных числа — \(n\), \(m\) и \(k\) (\(k\le n\le2000\), \(1\le m\le10^5\), \(1\le k\le40\)). Далее следуют \(m\) строк, каждая из которых описывает один трубопровод. Трубопровод задаётся двумя целыми числами — порядковыми номерами станций, которые он соединяет. Станции пронумерованы от 1 до \(n\). Гарантируется, что к любой станции подведён хотя бы один трубопровод и между любыми двумя станциями проложено не более одного трубопровода. Числа в каждой строке разделены пробелами.
Выходные данные
В первую строку выходного файла выведите слово «Yes», если требуемое расположение датчиков существует, в противном случае — слово «No». В случае положительного ответа выведите во вторую строку выходного файла \(k\) различных целых чисел — номера станций, на которых необходимо установить датчики. Номера можно выводить в любом порядке. Если существует несколько подходящих расположений датчиков, выведите любое из них. Разделяйте числа во второй строке пробелами.
Система оценивания
Решения, корректно работающие при \(n\le100\) и \(k\le10\), будут оцениваться из 60 баллов.
Примеры
Входные данные
9 12 4 1 2 2 3 1 4 4 5 1 6 6 7 1 8 8 9 2 5 4 7 6 9 8 3
Выходные данные
Yes 2 4 6 8
Входные данные
8 12 4 7 4 7 5 3 1 2 8 4 3 3 2 6 1 1 2 1 4 6 5 8 6 8 7
Выходные данные
No
Входные данные
4 3 1 3 1 3 2 3 4
Выходные данные
Yes 3
Страница:
1
Отображать по:
Выбрано
:
|