Страница: 1 Отображать по:

#19

Треугольная реформа

Темы: [Динамическое программирование по профилю] [Многоугольники. Выпуклые оболочки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2006, 2 день, Задача C ]

Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.

Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.

Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.

Формат входных данных

В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.

Формат выходных данных

В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.

Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.

В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.

Если искомых разбиений несколько, выведите любое из них.

Примеры

Входные данные	Выходные данные	Рисунок к тесту
4 0 0 1 0 1 1 0 1	2 1 1 1 0 0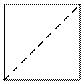
10 -6 0 0 2 6 0 3 3 6 4 2 4 0 6 -2 4 -6 4 -3 3	4 3 2 4 -2 4 0 2 3 3 -3 3 0 2

#3400

Распил бревен

Темы: [Многоугольники. Выпуклые оболочки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2011, Задача H ]

Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.

Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:

\(x_0 < x_1 < x_2 < \dots < x_N\);

\(x_i = 0\) для некоторого \(0 < i < N\);

\(y_0 = y_N = 0\);

для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).

С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:

основание треугольника лежит на оси абсцисс;

основание симметрично относительно начала координат;

треугольник полностью лежит внутри каждого из измеренных сечений заготовки.

Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.

Входные данные

Первая строка входного файла содержит целое число \(K\) – количество измеренных сечений.

Далее следуют описания каждого из \(K\) сечений. В первой строке описания сечения содержится число \(N_K\) – количество звеньев ломаной. За ней следуют (\(N_K + 1\)) строк, каждая из которых содержит пару целых чисел \(x_i\) и \(y_i\) – координаты вершин ломаной сечения в порядке их следования.

Выходные данные

Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).

Подзадачи и система оценки

Данная задача содержит пять подзадач.

Подзадача 1 (20 баллов)

\(K = 1\), \(N_1 \leq 15\), координаты вершин по модулю не превышают 20.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 2 (10 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Подзадача 3 (20 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\).

Подзадача 4 (10 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Подзадача 5 (40 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\).

Каждый тест для данной подзадачи оценивается отдельно.

Примеры

Входные данные

Выходные данные

25.0

#113546

Тигры

Темы: [Многоугольники. Выпуклые оболочки] [Интерактивные задачи]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 1 день, Тигры ]

В заповеднике живут q тигров. Чтобы следить за положением тигров на территории заповедника, используются ошейники с радиомаяком. Ошейник у каждого тигра имеет радиомаяк с уникальным сигналом. Система обнаружения настраивается на приём сигнала радиомаяка от i-го тигра последовательно для i от 1 до q.

Для приёма сигнала на территории заповедника установлено n приёмников в точках с координатами (x₁, y₁), ..., (x_n, y_n). Система обнаружения позволяет сотруднику заповедника за один запрос выбрать любые m (3 ≤ m ≤ n) приёмников. Выбранные приёмники должны являться вершинами выпуклого многоугольника. Система определяет, находится ли радиомаяк i-го тигра внутри этого многоугольника.

Сотрудник заповедника должен локализовать положение каждого тигра. Положение i-го тигра считается локализованным, если удалось определить такое множество приёмников, являющихся вершинами выпуклого многоугольника, что внутри этого многоугольника находится тигр, но нет других приёмников.

Для того, чтобы локализовать положение каждого из тигров, сотруднику разрешается сделать не более k запросов.

После того как положение i-го тигра локализовано, система автоматически переходит к приёму сигналов от следующего тигра, пока положение всех q тигров не будет локализовано.

Гарантируется, что никакие три приёмника не лежат на одной прямой, и ни один тигр не находится на прямой, проходящей через два приёмника. Гарантируется, что существует хотя бы один выпуклый многоугольник с вершинами в приёмниках, внутри которого находится тигр.

Требуется написать программу, которая взаимодействует с программой жюри и локализует положение каждого тигра.

Протокол взаимодействия

Это интерактивная задача.

Сначала на вход подаётся информация об установленных в заповеднике приёмниках и количестве тигров.

Первая строка входных данных содержит целое число n — количество приёмников (3 ≤ n ≤ 5 000). Последующие n строк описывают координаты приёмников, j-я из этих строк содержит два целых числа x_j и y_j — координаты j-го приёмника ( - 10⁹ ≤ x_j, y_j ≤ 10⁹). Следующая строка содержит число целое число q — количество тигров (1 ≤ q ≤ 2000).

Для локализации положения тигров необходимо выполнять запросы к системе обнаружения, роль которой выполняет программа жюри.

Для каждого теста зафиксировано число k — максимальное количество запросов к системе обнаружения для локализации положения одного тигра. Гарантируется, что k запросов достаточно, чтобы решить задачу для соответствующих данных. Это число не сообщается программе-решению, но ограничения на него в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов для определения местоположения одного из тигров, на этом тесте она получает в качестве результата тестирования «Неверный ответ».

Запрос к системе обнаружения начинается с символа «?», за которым следует целое число m — количество выбранных в запросе приёмников (3 ≤ m ≤ n), и m различных целых чисел p_i — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ p_i ≤ n).

В ответ программа получает строку «Yes», если тигр находится внутри многоугольника, образованного приёмниками с номерами p₁, ..., p_m, и строку «No» в противном случае.

После того, как положение тигра локализовано, программа-решение должна вывести строку, начинающуюся с символа «!», за которым следует целое число m — количество выбранных приёмников (3 ≤ m ≤ n), и m различных целых чисел p_i — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ p_i ≤ n). Эта строка означает, что внутри выпуклого многоугольника, образованного приёмниками с номерами p₁, ..., p_m, находится тигр и нет других приёмников.

Ответное сообщение от программы жюри отсутствует, и программа-решение должна немедленно приступать к поиску следующего тигра. Локализовав положение тигра с номером q, программа-решение должна завершить работу.

Тигры не перемещаются во время работы системы обнаружения. Координаты тигров в каждом тесте фиксированы и не меняются в процессе тестирования.

Если существует несколько правильных многоугольников, локализующих положение тигра, можно вывести любой из них.

На рисунке продемонстрирована процедура локализации положения каждого из тигров из приведенного ниже примера.

Примечание

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.

Страница: 1 Отображать по:

Выбрано

Отменить

Добавить в контест