Напомним, что важнейшей задачей молекулярной биологии является изучение различных белков. В общем случае один и тот же белок имеет одну из четырех форм (первичная, вторичная, третичная и четвертичная структура), простейшей с точки зрения химии является первичная, которую мы и рассмотрим.
Белок представляет собой последовательность аминокислот, соединенных пептидной связью (эта связь одинакова между любыми двумя аминокислотами, поэтому рассматриваться она не будет). Аминокислота, как следует из названия, — это органическое соединение, в молекуле которого одновременно содержатся карбоксильные и аминные группы. Для простоты будем считать, что аминокислота состоит из химических элементов, каждый элемент будем обозначать маленькой латинской буквой, таким образом, аминокислота однозначно определяется строкой из нескольких латинских букв. Безусловно, не любая последовательность элементов является аминокислотой.
Для каждого организма известен большой список аминокислот, которые могут быть синтезированы в организме такого типа. Для удобства транскрипции (это один из этапов синтеза РНК), ни одна аминокислота не является началом другой.
Одна из часто встречающихся задач заключается в том, чтобы понять, мог ли данный белок быть синтезирован в данном организме (это позволяет понять по белку, где он был синтезирован: у человека, у гриба и пр.). Для этого нужно проверить, все ли аминокислоты, из которых он состоит, могли быть синтезированы. Однако, часто белок содержит лишние элементы (например, к белку из-за обилия атомов водорода очень часто присоединяются молекулы воды), поэтому задача сводится к изучению фрагментов этого белка. Проводят как отдельные проверки каких-то фрагментов, так и целые серии проверок случайных фрагментов.
Более формально, вам дан словарь из аминокислот, каждая из которых представляет собой строку из маленьких латинских букв, и белóк, который также представляет собой строку из маленьких латинских букв. Необходимо ответить на несколько вопросов вида «мог ли фрагмент белка с позиции l по r быть синтезирован из данных аминокислот», т. е. можно ли данный фрагмент разбить на слова из словаря. В случае положительного ответа, необходимо предъявить минимальное количество слов в таком разбиении.
В первой строке входного файла содержится одно число N — количество аминокислот. Далее следует N непустых строк, каждая из которых является описанием аминокислоты. Суммарная длина строк S не превосходит 106.
В следующей строке содержится исходный белок, длина L которого не превосходит 106.
Далее содержится число M — количество простых запросов (0 ≤ M ≤ 105). Каждый простой запрос описывается двумя числами — l и r, (1 ≤ l ≤ r ≤ L), обозначающими искомый фрагмент [l, r], который необходимо разбить.
Далее содержится число K — количество запросов-серий (0 ≤ K ≤ 105, в некоторых группах тестов запросы-серии отсутствуют и K = 0).
Каждая серия описывается восемью целыми числами T, A, B, C, D, E, l1, r1 (1 ≤ A, B, C, D ≤ 100,
1 ≤ T, E, l1, r1 ≤ 107). Такая серия описывает T простых запросов. Запрос с номером i выглядит как фрагмент 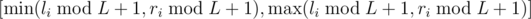 . Числа li и ri для i ≥ 2 определяются следующим образом. Пусть ans обозначает ответ на запрос с
номером i - 1 в этой серии. Тогда
. Числа li и ri для i ≥ 2 определяются следующим образом. Пусть ans обозначает ответ на запрос с
номером i - 1 в этой серии. Тогда 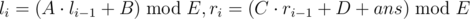 . Суммарное число запросов в сериях не превосходит
107.
. Суммарное число запросов в сериях не превосходит
107.
Все строки во входном файле состоят только из маленьких латинских букв. Гарантируется. что ни одна аминокислота не является префиксом другой.
Для каждого простого запроса выведите единственное число — минимальное число аминокислот, на которое разбивается соответсвующий фрагмент. В случае, если разбиения не существует, ответом на запрос является число - 1. Для каждой серии выведите одно число — сумму ответов на все запросы, для которых ответ существует (то есть не равен - 1), взятую по модулю E.
2
abra
cadabra
abracadabra
6
1 4
8 11
4 8
5 11
1 11
3 6
0
1
1
-1
1
2
-1
2
ab
ba
ababab
0
1
10 1 2 3 4 5 6 7
3
Тесты состоят из пяти групп.
- Тесты 1–2, из условия, оцениваются в 0 баллов.
- В тестах этой группы общая длина словарных аминокислот S не превосходит 5 000, длина белка L не превосходит 5 000, число простых запросов M не превосходит 5 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарная длина аминокислот S не превосходит 500 000, длина белка L не превосходит 5 000, число простых запросов M не превосходит 5 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарная длина аминокислот S не превосходит 500 000, длина белка L не превосходит 100 000, число простых запросов M не превосходит 100 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 20 баллов, баллы начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов всех предыдущих групп. Некоторые тесты этой группы объединяются в подгруппы, тесты за каждую подгруппу ставятся только при прохождении всех тестов подгруппы.
В новой телевизионной игре участник должен попасть извне в центр системы вложенных крепостей. Каждая крепость представляет собой выпуклый многоугольник, крепости друг друга не касаются. Центральная точка имеет координаты (0, 0) и находится в самой внутренней крепости. Каждая крепость имеет несколько «дверей». Для каждой двери известно время, затрачиваемое на проход через нее. Проходить через крепостную стену вне дверей нельзя. Скорость передвижения участника вне дверей постоянна и равна 1, то есть время передвижения на расстояние S равно S.
Участник изначально находится в одной из дверей внешнего многоугольника (он сам может выбирать, в какой). Его цель — добраться до точки (0, 0) как можно быстрее. Но в игре существует следующее ограничение: когда участник вошел в какую-то дверь, в качестве следующей двери он может выбрать только такую, которая сейчас находится вне зоны его прямой видимости. Если игрок смотрит вдоль стены, то он видит находящиеся в ней двери.
Требуется определить, может ли участник добраться до финиша, и если да, то за какое минимальное время он может это сделать при оптимальном выборе стартовой двери.
В первой строке входного файла задано единственное число N (1 ≤ N ≤ 105) — количество крепостей. Далее идут N блоков данных в следующем формате: в первой строке блока содержится число K (3 ≤ K ≤ 105) — количество вершин многоугольника, описывающего крепостную стену. За ней следуют K строк, в каждой из которых записано два числа x, y — координаты соответствующей вершины. В следующей строке идет число M (1 ≤ M ≤ 105) — число дверей, расположенных на границе этого многоугольника. Затем идут M строк, каждая из которых содержит три числа x, y, t — координаты двери и время прохода через нее. Все координаты целые, по модулю не превосходящие 109. Время прохода t — целое число, 0 ≤ t ≤ 106. Общее количество вершин многоугольников, а также общее число дверей не превосходит 3·105. Гарантируется, что каждая дверь находится на границе или в вершине соответствующего многоугольника.
Первый блок соответствует внешнему многоугольнику (тому, с которого участник начинает игру), второй — вложенному в него, ..., последний блок соответствует самому внутреннему многоугольнику.
Вершины многоугольников заданы в порядке обхода против часовой стрелки. Никакие три последовательные вершины не лежат на одной прямой. Двери могут быть заданы в произвольном порядке.
Гарантируется, что при i = 1, 2, ..., N - 1 каждая точка i + 1-го многоугольника находится строго внутри i-го. Все многоугольники содержат точку (0, 0).
Выведите одно число — минимальное время, за которое участник может добраться до финиша, с абсолютной или относительной точностью 10 - 6. Если участник не может закончить игру, выведите одно число «-1» (без кавычек).
2
4
4 3
-3 3
-3 -2
4 -2
2
-3 0 3
-2 3 2
4
1 2
-1 2
-1 -1
1 -1
3
0 2 10
0 -1 4
-1 2 1
11.236067
Тесты состоят из пяти групп.
- Тест из условия, оценивается в 0 баллов.
- В тестах этой группы суммарное количество вершин и дверей не превосходит 100, а каждая крепостная стена описывается прямоугольником со сторонами, параллельными осям координат. Эта группа оценивается в 20 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарное количество вершин и дверей не превосходит 100. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой группы. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарное количество вершин не превосходит 2000, суммарное количество дверей не превосходит 2000. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой и 2-й групп. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой, 2-ой и 3-ей групп. Каждый тест оценивается независимо от других.
Михаил придумал решение задачи аппаратного кодирования видео с помощью последовательно соединенных микроконтроллеров. Каждый микроконтроллер выполняет определенную часть задачи, после чего передает данные следующему микроконтроллеру (получается некий конвейер из микроконтроллеров). В устройстве используется N микроконтроллеров, которые должны быть соединены последовательно: первый со вторым, второй с третьим и т. д. По задумке, микроконтроллеры располагались на плате в одну горизонтальную линию.
Михаил заказал платы с микроконтроллерами на фабрике, однако получилось так, что микроконтроллеры вместо того, чтобы стоять последовательно, оказались в хаотичном порядке! Поскольку заказ был довольно дорогим, Михаил решил максимально использовать имеющуюся плату, т.е. последовательно соединить дорожками наибольшее количество микроконтроллеров в цепочку вида 1 - 2 - ... - m. Оставшуюся часть придется заказать заново.
Плата, на которой расположены микроконтроллеры, будет односторонней (все дорожки расположены на одной плоскости и, естественно, не могут пересекаться). Если в микроконтроллер дорожка со входным сигналом входит сверху, то дорожка с выходным сигналом должна выходить из него обязательно снизу, и наоборот. Микроконтроллеры расположены вплотную друг к другу (проложить между ними дорожку нельзя). Обойти линию микроконтроллеров дорожкой слева или справа также нельзя (только сверху или снизу). Сверху и снизу от линии микроконтроллеров плата имеет достаточные размеры и позволяет проложить любое число дорожек.
Помогите Михаилу определить, какое максимальное количество последовательных микроконтроллеров удастся соединить, начиная с первого.
В первой строке входного файла задано число N — длина полоски из микроконтроллеров.
Во второй строке задана перестановка из N чисел — порядок расположения микроконтроллеров.
Выведите единственное число — максимальное количество микроконтроллеров, которые удастся соединить последовательно, начиная с первого.
Тесты состоят из четырех групп.
- Тест 1, из условия, оценивается в 0 баллов.
- В тестах этой группы количество микроконтроллеров N не превосходит 5 000. Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы количество микроконтроллеров N не превосходит 100 000. Эта группа оценивается в 40 баллов, баллы начисляются только при прохождении всех тестов этой и предыдущей группы.
- В тестах этой группы количество микроконтроллеров N не превосходит 1 000 000. Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов из всех групп.
7 5 1 4 7 6 3 2
5