Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.
Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.
Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:
abc
acb
симпатичными являются все части, состоящие из одного квадратика (их 6), а также части
bc и a
cb и a
Напишите программу, которая по информации о шедевре Васи определит его стоимость.
В первой строке содержатся два числа N и M (1 ≤ N, M ≤ 100). В следующих N строках идут строки, состоящие из M маленьких латинских символов. Символ в i-й строке j-м столбце определяет цвет соответствующего квадратика картины.
Выведите стоимость шедевра — количество частей, симметричных относительно своего центра.
Комментарии к примерам тестов
Этот пример разобран в условии
Симпатичными являются шесть частей 1x1, одна часть 1x2 и сама картина.
Частичные ограничения
Первая группа состоит из тестов, в которых N, M ≤ 15. Данная группа оценивается в 30 баллов.
Вторая группа состоит из тестов, в которых N, M ≤ 50. Данная группа оценивается в 30 баллов.
2 3 abc acb
8
3 2 ab cc ba
8
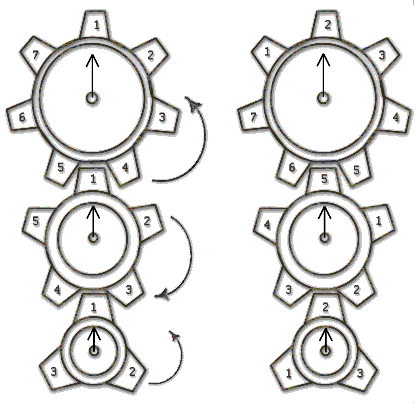На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a1,a2,a3), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.
Поступая и далее таким образом, Витя заметил, что после некоторого количества таких действий стрелки показывают на три первоначальных числа.
Теперь его очень интересует, как по двум данным тройкам чисел определить, принадлежат ли они к одной последовательности, то есть можно ли некоторым количеством поворотов перейти от первой тройки ко второй. Он попросил вас написать программу, которая отвечает на этот вопрос.
В первой строке содержатся четыре числа T, n, m, k (1 ≤ T ≤ 10, 1 ≤ n, m, k ≤ 1018) — количество пар троек, которые хочет проверить Витя и количества зубцов соответственно на первой, второй и третьей шестеренках.
В следующих T строках записаны шесть натуральных чисел a1, a2, a3, b1, b2, b3 (1 ≤ a1, b1 ≤ n, 1 ≤ a2, b2 ≤ m, 1 ≤ a3, b3 ≤ k).
Для каждой пары троек в выходной файл выведите YES, если обе тройки принадлежат одной последовательности, и NO иначе. Каждое слово должно быть в отдельной строке, в порядке, соответствующем входному файлу.
Комментарии к примерам тестов
1. В первой и второй парах вторая тройка получается из первой за один поворот первой шестеренки против часовой стрелки.
В третьем случае из второй конфигурации просто получить первую опять же одним поворотом первой шестеренки против часовой стрелки.
Очевидно, что тогда из первой можно каким-то образом получить вторую.
2. В первой паре тройки нельзя перевести друг в друга.
Во второй тройки переходят друг в друга при одном повороте.
3. (1, 1, 1) — (семь поворотов первой против часовой стрелки шестеренки) — (1, 4, 2) — (еще семь таких же поворотов) — (1, 2, 3) — (один поворот) — (2, 1, 1)
Частичные ограничения
Первая группа состоит из тестов, в которых произведение nmk ≤ 106.
Вторая группа состоит из тестов, в которых n, m, k ≤ 109.
Примечание
Не гарантируется, что описанную в условии задачи систему шестеренок и стрелок можно реально построить.
3 11 13 15 5 5 5 6 4 6 11 13 15 1 12 1 2 13 2 1 1 1
YES YES YES
2 2 2 2 1 1 1 1 1 2 1 1 1 2 2 2
NO YES
1 7 5 3 1 1 1 2 1 1
YES
С незапамятных времен граница страны Флатландия имеет форму N-угольника без самопересечений и самокасаний (необязательно выпуклого). В каждой из вершин этого многоугольника король построил по башне.
В целях увеличения обороноспособности государства на его территории король задумал построить Великий Флатландский Забор. По причине многолетней войны ресурсов хватает на строительство ровно K стен (неважно, какой длины). Каждая стена должна соединять ровно две башни по прямой и не должна даже частично выходить за пределы Флатландии. К тому же, Забор должен представлять собой не более чем K-угольник также без самопересечений и самокасаний (углов может оказаться и меньше, чем K, так как некоторые соседние стены могут лежать на одной прямой). Военный советник настаивает на том, что площадь защищенной области должна быть как можно больше.
Ваша задача — помочь спроектировать такой Забор.
В первой строке записаны два целых числа N и K (3 ≤ K ≤ N ≤ 230). В следующих N строках содержатся пары целых чисел — координаты башен в порядке обхода границы против часовой стрелки. Гарантируется, что никакие три последовательные башни не лежат на одной прямой. Все координаты не превосходят 1000 по абсолютной величине.
В первую строку запишите максимальную площадь, которую можно защитить Забором, с точностью до пяти знаков после десятичной точки. Во второй строке должно быть Q — количество выбранных башен.
Будем считать, что башни занумерованы числами от 1 до N в порядке перечисления их во входном файле. Во третью строку через пробел выведите номера Q башен, которые будут вершинами Забора, в порядке его обхода против часовой стрелки.
Частичные ограничения
Первая группа состоит из тестов, в которых N ≤ 20 и граница Флатландии представляет собой выпуклый многоугольник.
Вторая группа состоит из тестов, в которых N ≤ 20, но граница может быть уже любой.
3 3 0 0 1 0 0 1
0.50000 3 1 2 3
6 5 0 0 7 0 4 3 4 4 3 4 0 7
24.50000 5 1 2 3 5 6
4 3 0 0 1 3 0 2 -2 -2
2.00000 3 1 3 4
В настольном теннисе в результате каждой подачи разыгрывается одно очко. Подача переходит от игрока к игроку каждые 5 подач, т.е. первые пять раз подает первый игрок, затем 5 раз — второй, затем снова первый и т.д.
Партия играется до тех пор, пока кто-нибудь из игроков не наберет 21 очко. Тот, кто набрал 21 очко, признается победителем, и игра заканчивается.
Вася и Петя играли в игру, и забыли, кто должен подавать в данный момент. Однако они помнят, что первую подачу делал Вася, и счет в настоящий момент a:b (a очков у Васи и b очков у Пети). Напишите программу, которая по данным a и b будет определять, чья подача или устанавливать, что игра закончена.
Вводятся два числа a и b. Числа соответствуют реальному счету, т.е. оба числа целые, от 0 до 21 и не равны 21 одновременно.
Выведите одно из четырех сообщений:
· Vasya serves — если сейчас должен подавать Вася
· Petya serves — если сейчас должен подавать Петя
· Vasya wins — если игра завершена и выиграл Вася
· Petya wins — если игра завершена и выиграл Петя
4 1
Petya serves
15 0
Petya serves
21 12
Vasya wins
Возвращаясь с турслета, Вася пришел на станцию и хочет уехать в Москву. На станции не оказалось расписания электропоездов, но у Васи есть справочник, в котором указано время отправления поездов с конечных пунктов, а также время следования от каждого из конечных пунктов до станции, где находится Вася.
Помогите Васе определить, сколько ему придется ждать ближайшую электричку.
Сначала вводятся два числа, задающих часы и минуты прихода Васи на станцию.
Далее идет число \(N\) — количество конечных станций, от которых отправляются электрички, проходящие через Васину станцию (1≤\(N\)≤100).
Далее идет N блоков данных (по одному блоку для каждой станции). Сначала записано время \(T_i\) следования электрички от станции ее отправления до станции, где находится Вася. Время задается в минутах и выражается целым неотрицательным числом, не превышающим 1440.
Далее идет число \(M_i\), определяющее количество электричек в сутки, отправляющихся от этой станции (1≤\(M_i\)≤100). Далее идет \(M_i\) пар чисел, задающих времена отправления электричек от этой станции. Все времена указаны в возрастающем порядке.
Часы находятся в интервале от 0 до 23, минуты – от 0 до 59.
Считается, что все электропоезда ходят ежедневно. Т.е., например, если у нас только один пункт и только одна электричка, и с этого пункта она отправляется в 23.59 и идет до Васиной станции 61 минуту, то в 01.00 Вася может на ней уехать в тот день, когда он пришел на станцию (если он пришел не позднее 01.00), или на следующий день, если он придет позднее.
Гарантируется, что хотя бы одна электричка в сутки через Васину станцию проходит.
Выведите одно число — время в минутах, которое Васе придется ждать ближайшую электричку. Считается, что если Вася и электричка приходят на станцию одновременно, то Вася успевает на эту электричку и время ожидания 0.
15 57 2 5 2 15 50 19 30 30 1 15 43
16
18 0 1 0 1 15 0
1260
18 0 2 0 1 18 0 10 1 17 50
0