Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
На плоскости дано N горизонтальных отрезков. Будем говорить, что прямая пересекает отрезок, если у этой прямой и этого отрезка есть хотя бы одна общая точка (в том числе прямая пересекает отрезок, если она проходит через один из его концов). Требуется найти прямую, пересекающую все отрезки, или установить, что такой нет.>
В первой строке входного файла находится единственное число N. В каждой из следующих N строк содержатся по три целых числа Pi, Qi, Ri, описывающих отрезки: соответствующий отрезок соединяет точки (Pi, Ri) и (Qi, Ri). Никакие два отрезка не лежат на одной прямой.
1≤N≤10000, Pi<Qi, все числа по модулю не превосходят 10000.
В случае, если искомая прямая существует, выведите в выходной файл коэффициенты ее уравнения (будем задавать прямую уравнением вида A∙x+B∙y+C=0, где x, y – координаты точек прямой, A, B, C – такие коэффициенты, что указанному уравнению удовлетворяют все точки прямой, и только они; соответственно, чтобы задать прямую, нужно задать три числа – A, B, C).
Коэффициенты уравнения должны быть целыми и не должны превосходить по модулю 109 (гарантируется, что при наличии решения такие A, B, C существуют).
Если прямой не существует, выведите в выходной файл сообщение “No solution” (без кавычек).
3 0 1 0 0 1 1 0 1 2
1 0 0
5 0 2 0 2 4 1 1 3 2 1 3 -1 1 3 -2
3 -1 -5
3 0 1 0 1 2 1 -2 -1 2
No solution
Заданы целые числа X, Y, P, Q (–10100 <= X, Y, P, Q <= 10100). Требуется проверить равенство XY = PQ. Напомним, что ab определяется следующим образом:
Во входном файле записаны числа X, Y, P, Q, каждое в отдельной строке.
Выведите слово correct, если данное равенство для полученных входных данных выполняется, или incorrect, если равенство не выполняется, или хотя бы одна из степеней не определена.
2 4 4 2
correct
2 3 3 2
incorrect
Вася и Петя играют в увлекательную игру. Вася выписал подряд числа от 1 до N. А Петя выписал P пар чисел (Ai, Bi).
Теперь Вася преобразует имеющуюся последовательность чисел - он меняет местами числа в этой последовательности. Если некоторая пара чисел (Ai, Bi) выписана Петей, то Вася имеет право в любой момент взять числа из последовательности, стоящие на местах Ai и Bi и поменять их местами.
Например, если N=5. Тогда изначально Васей выписана последовательность
1 2 3 4 5
Пусть Петя написал две пары чисел: (1,2) и (2,5). Тогда Вася в любой момент может менять числа, стоящие на 1 и 2 местах, или же числа, стоящие на 2 и 5 местах.
Например, он может последовательно получить следующие последовательности:
2 1 3 4 5 (поменяв числа на 1 и 2 местах)
2 5 3 4 1 (поменяв числа на 2 и 5 местах)
5 2 3 4 1 (поменяв числа на 1 и 2 местах).
Пете не показываются промежуточные последовательности, а выписывается лишь полученная на последнем шаге.
От Пети требуется проверить, мог ли Вася получить такую последовательность не нарушая правил игры, и если мог, то указать, в результате какой последовательности обменов (при этом не требуется, чтобы число обменов было минимально возможным).
Напишите программу, которая поможет Пете справиться с этой задачей.
Сначала записано число N (1≤N≤100) – количество чисел в последовательности. Дальше идет N чисел – последовательность, полученная Васей (в последовательности каждое из чисел от 1 до N встречается ровно один раз).
Далее идет число P (0≤P≤10000) – количество пар чисел, выписанных Петей. Далее записано P пар чисел (каждое число пары – из диапазона от 1 до N).
В первую строку выходного файла выведите сообщение YES (если такая последовательность могла быть честно получена Васей) и NO (если такую последовательность Вася не мог получить, не нарушая правил игры).
В случае, если такая последовательность могла быть получена, далее выведите способ ее получения (если вариантов несколько, выведите любой из них). Сначала выведите число K – количество операций обмена (оно не должно превышать 100000), а затем K пар чисел, задающих номера мест, на которых стоят обмениваемые элементы (числа в паре могут быть выданы в любом порядке). Гарантируется, что если решение существует, то существует решение с числом обменов, не превышающим 100000.
5 5 2 3 4 1 2 1 2 2 5
YES 3 1 2 2 5 1 2
5 2 3 4 5 1 2 1 2 2 5
NO
SMS-сообщения на мобильном телефоне марки MOBILO набираются только заглавными английскими буквами. Для набора буквы нужно нажать кнопку, на которой эта буква написана, при этом если эта буква написана первой, то кнопку нужно нажать один раз, если второй – то два раза и т.д. Устройство клавиатуры телефона приведено на рисунке. 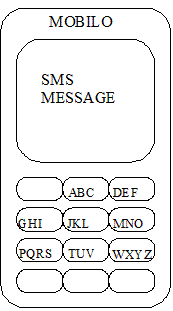
Таким образом, чтобы набрать слово SMS, нужно нажать следующие кнопки:
<PQRS> <PQRS> <PQRS> <PQRS> <MNO> <PQRS> <PQRS> <PQRS> <PQRS>
Для набора двух букв, которые находятся на одной кнопке, при наборе нужно сделать паузу между их вводом. Например, чтобы набрать BA, нужно два раза нажать кнопку <ABC>, затем сделать паузу и затем нажать кнопку <ABC> еще раз.
Если на кнопке написано три буквы, то как только эта кнопка нажата три раза подряд, последняя из написанных на ней букв сразу же добавляется в сообщение, а дальнейшие нажатия на эту кнопку воспринимаются как ввод следующей буквы. То же самое, если на кнопке написано 4 буквы. Таким образом, 4-х кратное нажатие на кнопку <ABC>, затем пауза, и затем нажатие на эту кнопку еще раз приведет к вводу текста CAA.
К сожалению, в силу произошедшего глюка, телефон стал иногда игнорировать паузы при вводе, а, иногда, наоборот, вести себя так, как будто была пауза тогда, когда паузы не было. Например, при вводе слова MOSCOW могло в итоге (как один из вариантов) получиться слово OMSCMNW.
Вы получили SMS-сообщение, набранное на этом телефоне. Известно, что изначально оно состояло из N символов. Напишите программу, которая определит количество вариантов исходных сообщений, которые при вводе могли превратиться в то, что вы получили (если вариантов окажется 0, то это будет означать, что у телефона сломалось что-то еще).
Сначала записана длина исходного сообщения N (1≤N≤80). Вторая строка содержит полученное SMS-сообщение – последовательность не более чем из 80 заглавных латинских букв.
Выведите одно число – количество вариантов исходного сообщения.
4 MAMA
1
2 WWW
2
10 MAMA
0
В тридесятом царстве в новогодние праздники все лягушки собираются на самом большом болоте, чтобы поиграть в замечательную игру. Всего в этом царстве живет N зеленых лягушек и M коричневых. Для игры они выбирают на болоте N + M + 1 кочку, на первые N кочек слева садятся зеленые лягушки, а на последние M — коричневые (т. е. между ними находится одна кочка, на которой никто не сидит). Зеленые лягушки садятся лицом к коричневым лягушкам, а коричневые — к зеленым. Кочки настолько маленькие, что развернуться на них, не свалившись в болото, совершенно не возможно. Поэтому лягушки могут двигаться только вперед и не могут разворачиваться.
На каждом ходе игры одна из лягушек перепрыгивает с той кочки, где она сидит, на свободную кочку. При этом лягушка может прыгнуть на соседнюю кочку вперед, либо перепрыгнуть через одну кочку, если соседняя занята.
Чтобы праздник удался, зеленые лягушки должны оказаться на последних кочках, а коричневые — на первых. Порядок, в котором лягушки окажутся на кочках, не важен. Так как на праздник каждый раз приходит разное количество лягушек, то им каждый год приходится придумывать очередность прыжков. Напишите программу, которая поможет лягушкам составить план прыжков.
Поиграть в эту игру для случая N=M=3 можно по ссылке:
Во входном файле записаны два числа N и M (1≤N≤1000, 1≤M≤1000) – количество зеленых и коричневых лягушек соответственно.
Выведите последовательность прыжков лягушек для достижения поставленной цели. Каждый прыжок можно задать одним числом — номером прыгающей лягушки (поскольку свободная кочка всегда ровно одна). Пронумеруем всех лягушек в соответствии с их начальным положением. Зеленые лягушки будут пронумерованы числами от 1 до N, а коричневые — с N+1 до N+M в порядке слева направо.
В первую строку выходного файла выведите число K — количество прыжков. K не должно превышать 107. Далее выведите K чисел — номера лягушек.
Если же достичь требуемой рассадки лягушек нельзя, выведите одно число –1.
2 1
5 2 3 2 1 3