#1036

Выборы жрецов

Темы: [Цикл for]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача B ]

В стране Олимпиадии снова выборы.

Страна состоит из маленьких графств. Графства объединяются в конфедерации. Каждая конфедерация раз в год выбирает себе покровителя – одного из 200 жрецов. Этот ритуал называется Великими Перевыборами Жрецов и выглядит так: конфедерации одновременно подают заявления (одно от конфедерации) в Совет Жрецов о том, кого они хотели бы видеть своим покровителем (если заявление не подано, то считают, что конфедерация хочет оставить себе того же покровителя). После этого все заявки удовлетворяются. Если несколько конфедераций выбирают одного и того же Жреца, то они навсегда объединяются в одну. Таким образом, каждый Жрец всегда является покровителем не более чем одной конфедерации. Требуется написать программу, позволяющую Совету Жрецов выяснить номер Жреца-покровителя каждого графства после Великих Перевыборов. В Совете все графства занумерованы (начиная с 1). Все Жрецы занумерованы числами от 1 до 200 (некоторые из них сейчас могут не быть ничьими покровителями).

Входные данные

Во входном файле записано число N – количество графств в стране (1N5000) – и далее для каждого графства записан номер Жреца-покровителя конфедерации, в которую оно входит (графства считаются по порядку их номеров). Затем указаны заявления от конфедераций. Сначала записано число M – количество поданных заявлений, а затем M пар чисел: первое число – номер текущего Жреца-покровителя, второе – номер желаемого Жреца-покровителя.

Все числа во входном файле разделяются пробелами и (или) символами перевода строки.

Выходные данные

В выходной файл вывести для каждого графства одно число – номер его Жреца-покровителя после Великих Перевыборов. Сначала – для первого графства, затем – для второго и т.д.

Примеры

Входные данные

7
1 1 5 3 1 5 1
2
5 1
1 3

Выходные данные

3 3 1 3 3 1 3

#1037

Представление чисел

Темы: [НОД и алгоритм Евклида] [Целые числа]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача C ]

Необходимо представить N в виде A+B, так, что НОД(A, B) максимален.

Дано натуральное число N. Требуется представить его в виде суммы двух натуральных чисел A и B таких, что НОД (наибольший общий делитель) чисел A и B — максимален.

Ограничение по времени выполнения программы - 1 секунда, ограничение по используемой памяти - 64 мегабайта.

Входные данные

Во входном файле записано натуральное число N (2≤N≤10⁹)

Выходные данные

В выходной файл выведите два искомых числа A и B. Если решений несколько, выведите любое из них.

Примеры

Входные данные

Выходные данные

5 10

Входные данные

Выходные данные

8 8

#1038

Гексагон

Темы: [Условный оператор (if)]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача D ]

Поле для игры в новую игру "Гексагон" разбито 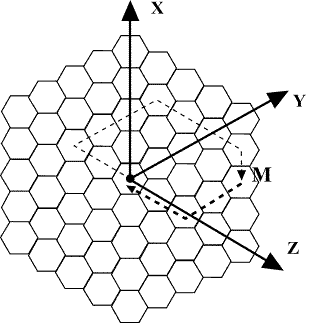на шестиугольники (см. рисунок). Игрок, стартуя из некоторого начального шестиугольника, сделал несколько ходов. Каждый ход заключается в премещении фишки в соседний шестиугольник (имеющий с тем, где находилась фишка до начала хода, общую сторону) — тем самым, ход делается вдоль одного из направлений X, Y или Z (см. рисунок). Игрок записал все свои ходы, причем если фишка двигалась вдоль какого-либо направления несколько раз подряд, то в записи это обозначается указанием направления и количества ходов, которые были сделаны.

Напишите программу, которая найдет кратчайший (по количеству совершаемых ходов)путь в начальную клетку из той, где фишка оказалась после ходов игрока.

Входные данные

В первой строке входного файла записано число N — количество строк в записи перемещений фишки (1N100). Далее идет N строк с записью ходов: в каждой строке записана сначала большая буква X, Y или Z, задающая направление, затем пробел, и число, задающее количество ходов в данном направлении (число может быть и отрицательным, если игрок перемещал фишку параллельно оси, но в направлении, противоположном направлению оси). Все числа по модулю не превышают 200.

Выходные данные

В выходной файл выведите описание кратчайшего пути обратно в начальную клетку в том же формате, в каком описание задано во входном файле (за исключением ограничений). Все числа, определяющие количество ходов в каком-либо направлении, должны быть ненулевыми.

Примеры

Входные данные

4
Z -2
Y 3
Z 3
X -1

Выходные данные

#1040

Кубическое уравнение

Темы: [Целые числа]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача F ]

Напишите программу, которая будет искать все целые X, удовлетворяющие уравнению

AX³ + BX² + CX + D = 0,

где A, B, C, D — данные целые числа.

Входные данные

Во входном файле записаны четыре целых числа: A, B, C, D. Все числа по модулю не превышают 210⁹.

Выходные данные

В выходной файл выведите сначала количество решений этого уравнения в целых числах, а затем сами корни в возрастающем порядке. Если уравнение имеет бесконечно много корней, выведите в выходной файл одно число –1 (минус один).

Примеры

Входные данные

1 0 0 -27

Выходные данные

1
3

Входные данные

0 1 2 3

Выходные данные

#1041

Скорая помощь

Темы: [Целые числа] [Перебор с отсечением]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2005, Задача G ]

Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры K₁, а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру K₂, которая расположена в подъезда P₂ на этаже N₂. Известно, что в доме M этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда P₁ и номер этажа N₁ квартиры K₁.

Входные данные

Во входном файле записаны пять положительных целых чисел K₁, M, K₂, P₂, N₂. Все числа не превосходят 1000.

Выходные данные

Выведите два числа P₁ и N₁. Если входные данные не позволяют однозначно определить P₁ или N₁, вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).

Примеры

Входные данные

89 20 41 1 11

Выходные данные

2 3

Входные данные

11 1 1 1 1

Выходные данные

0 1

Входные данные

3 2 2 2 1

Выходные данные

-1 -1