Страница: << 1 2 Отображать по:
#1030
Побег с космической станции
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Представьте, что вы состоите на службе во внешней разведке Межгалактического Альянса Республиканских Сил (МАРС). Одному из агентов разведки крупно не повезло, и он был захвачен на засекреченной космической базе. К счастью, внешней разведке МАРС удалось заполучить план этой базы. И вот теперь вам поручено разработать план побега.

База представляет собой прямоугольник размером NхM, со всех сторон окружённый стенами, и состоящий из квадратных отсеков единичной площади. База снабжена K выходами, до одного из которых агенту необходимо добраться. В некоторых отсеках базы находятся стены. Ваш агент может перемещаться из отсека в любой из четырех соседних с ним, если в том отсеке, куда он хочет переместиться, нет стены.

Кроме того, база снабжена системой гипертуннелей, способных перемещать агента из одного отсека базы (вход в гипертуннель) в другой (выход из гипертуннеля). Когда агент находится в отсеке, где есть вход в гипертуннель, он может (но не обязан) им воспользоваться.

Начальное положение вашего агента известно. Вам необходимо найти кратчайший путь побега (то есть путь, проходящий через минимальное количество отсеков).

Входные данные

В первой строке входного файла записаны числа N и M (2≤N≤100, 2≤M≤100), задающие размеры базы: N — количество строк в плане базы, M — количество столбцов. Во второй строке записаны начальные координаты агента XA,YA (1≤XA≤N, 1≤YA≤M). Первая координата задает номер строки, вторая — номер столбца. Строки нумеруются сверху вниз, столбцы слева направо.

Далее следуют N строк по M чисел, задающих описание стен внутри базы: 1 соответствует стенке, 0 — её отсутствию.

Далее в отдельной строке записано число H (0≤H≤1000) — количество гипертуннелей. В последующих H строках идут описания гипертуннелей. Каждый гипертуннель задается 4 числами: X1, Y1, X2, Y2 (1≤X1,X2≤N; 1≤Y1,Y2≤M) — координатами входа и выхода гипертуннеля. Никакие два гипертуннеля не имеют общего входа.

После этого в отдельной строке следует число K (1≤K≤10) — количество выходов с базы. В последующих K строках идут описания выходов с базы. Каждый выход задается двумя координатами X и Y (1≤X≤N; 1≤Y≤M).

Гарантируется, что начальные координаты агента не совпадают ни с одним из выходов и он не стоит в отсеке, занятом стеной. Никакие входы и выходы гипертуннелей, а также выходы с базы не находятся в отсеках, занятых стенами. Никакой вход в гипертуннель не совпадает с выходом с базы

Выходные данные

Если побег невозможен, выведите единственную строку с надписью "Impossible". В противном случае в первой строке выдайте число L - количество отсеков в кратчайшем пути побега. В последующих L строках последовательно выведите координаты отсеков кратчайшего пути побега. Если решений несколько, то выведите любое из них.

Примеры
Входные данные
4 5
2 1
0 0 0 0 0 
0 1 0 0 0 
0 0 0 0 0 
0 0 0 0 0 
2
1 2 1 4
3 1 1 4
1
2 4
Выходные данные
4
2 1
3 1
1 4
2 4
#1032
Узор
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

В комнате решили сделать паркетный пол. Причем есть задумка выложить на полу некоторый узор.

Плитки паркета, которыми выкладывается пол комнаты, состоят из квадратиков 1x1, каждый из которых может быть либо белым, либо черным. В свою очередь, комната имеет размеры NxM. На плане комнаты указано, какой квадрат комнаты какого цвета должен быть.

Существует несколько форм паркетных плиток:

Квадратики одной паркетной плитки могут быть окрашены по-разному. Может существовать несколько типов плиток одинаковой формы, но окрашенных по-разному. Плитки разных типов могут иметь разную стоимость. Количество плиток каждого типа не ограничено. Плитки разрешается как угодно поворачивать (на углы, кратные 90 градусам). Не разрешается разламывать плитки, а также класть их лицевой стороной вниз.

Изначально, какая-то часть пола может уже быть выложена плиткой.

Требуется определить минимальную стоимость плитки, необходимой для того, чтобы замостить оставшуюся часть комнаты.

Входные данные

В первой строке входного файла записаны три числа: N, M (размеры комнаты) и K (количество доступных видов плитки). 1≤N≤8, 1≤M≤8, 1≤K≤10. Далее идет описание желаемой раскраски пола. Описание представляет собой N строчек по M чисел в каждой, где 0 обозначает белый цвет, 1 — черный, 2 — то, что квадрат уже выложен плиткой. В последних K строчках находятся описания доступных типов плитки в следующем формате:

<форма> <стоимость> <окраска>

<Форма> — это число от 1 до 4, описывающее форму плитки (см. рисунок выше)

<Стоимость> — это натуральное число, не превосходящее 10000, задающее стоимость одной плитки такого типа

<Окраска> — это от одного до трех чисел 0 или 1. Количество чисел совпадает с количеством квадратиков, из которых состоит плитка. Числа задают цвета квадратиков плитки в том порядке, в каком квадратики пронумерованы на рисунке.

Выходные данные

В выходной файл выведите единственное число — минимальную стоимость укладки или –1, если требуемым образом уложить плитку невозможно.

Примеры
Входные данные
4 3 3
2 2 2
2 0 0
2 1 2
2 2 2
2 10 0 0
1 5 1
4 6 0 0 1
Выходные данные
15
#1033
Склад
  

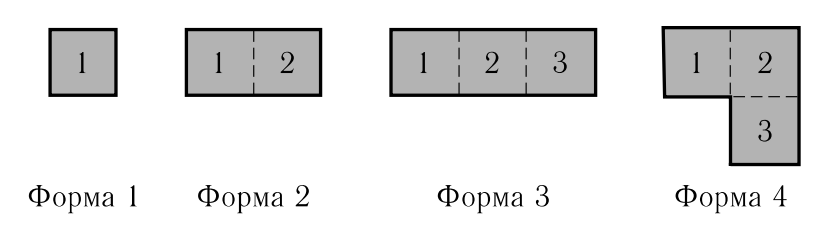
Склад конторы MacroHard представляет собой прямоугольную комнату размером NxM. На складе нарисована разметка, состоящая из линий, параллельных стенам склада, которые разбивают его на NxM квадратов 1x1.

Фирма выпускает высокотехнологичное оборудование, используемое в самых различных областях жизнедеятельности. Исторически сложилось так, что все изделия, выпускаемые этой компанией, имеют форму равнобедренного прямоугольного треугольника. При этом ассортимент изделий столь велик, что бывают изделия практически любых размеров.

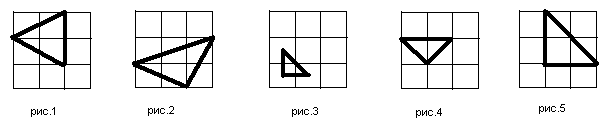
Размещать изделия на складе разрешается только так, чтобы хотя бы одна сторона изделия была параллельна какой-то из стен склада, и, вдобавок, все углы изделия находились в точках пересечения линий разметки склада. Рисунки 1,2,3 иллюстрируют неправильное положение изделий, а 4,5 – правильное.

Руководство фирмы узнало, что склад планирует посетить Комиссия по неэффективному использованию складских помещений. Чтобы избежать выплаты крупного штрафа, фирма решила в срочном порядке поместить на склад изделия так, чтобы на складе не осталось свободного места. При этом было решено, что продукция, которая уже находится на складе, перемещаться не будет.

Напишите программу, которая определит, какое минимальное количество изделий можно добавить на склад, чтобы на нем не осталось свободного места.

Входные данные

В первой строке входного файла записаны три целых числа: N, M (размеры склада) и K (количество изделий, которые уже находятся на складе). Следующие K строк содержат по 6 целых чисел — координаты углов соответствующего изделия. Система координат введена так, что оси координат параллельны стенам склада и при этом один из углов склада имеет координаты (0,0), а противоположный — (N,M).

Ограничения

1N4, 1M4

Выходные данные

Первая строка выходного файла должна содержать одно число T — минимальное количество изделий, которые необходимо добавить, чтобы полностью заполнить склад. Каждая из следующих T строк должна содержать по 6 чисел — координаты углов изделий.

Примеры
Входные данные
3 2 0
Выходные данные
5
0 0 0 2 2 0 
0 2 2 0 2 2 
2 0 2 2 3 1 
2 0 3 0 3 1 
2 2 3 1 3 2
#1034
Кубическая гостиница
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В связи с проведением межпланетного шашечного турнира было принято решение о строительстве орбитальной гостиницы. Она должна была представлять собой большой куб из N×N×N блоков – маленьких кубиков 1×1×1, и каждый блок должен был быть окрашен снаружи со всех сторон в какой-то один цвет. При этом некоторые блоки могли быть покрашены в один и тот же цвет.

Через год были сделаны фотографии гостиницы с каждой из 6 сторон: спереди, слева, сзади, справа, сверху, снизу. За год эксплуатации могло случиться так, что из-за непрочного крепления некоторые блоки, из которых была построена гостиница, оторвались и улетели в открытый космос. Комиссия по восстановлению гостиницы хочет по сделанным снимкам установить максимальное возможное количество оставшихся блоков.

Итак, вам необходимо по видам гостиницы (куба N×N×N, из которого, возможно, выкинуты некоторые кубики 1×1×1) с 6 сторон определить, из какого максимального количества блоков 1×1×1 она может состоять. Может оказаться так, что гостиница состоит из двух или более не связанных между собой частей.

Входные данные

В первой строке входного файла находится число N — размер гостиницы (1≤N≤10). На следующих N строках записаны виды гостиницы с 6 сторон (в следующем порядке: спереди, слева, сзади, справа, сверху, снизу). Каждый такой вид представляет собой таблицу N×N, в которой различными заглавными латинскими буквами обозначены различные цвета, а символом «.» (точка) — то, что в этом месте можно будет смотреть прямо сквозь гостиницу. Два последовательных вида отделяются друг от друга ровно одним пробелом в каждой из N строк.

Нижняя граница вида сверху соответствует верхней границе вида спереди, а верхняя граница вида снизу — нижней границе вида спереди. Для видов спереди, сзади и с боков верх и низ вида соответствуют верху и низу гостиницы.

Входные данные корректны, то есть во входном файле описано состояние, которое может получиться.

Выходные данные

Выведите в выходной файл одно число — искомое максимальное количество оставшихся блоков в гостинице.

Примеры
Входные данные
3
.R. YYR .Y. RYY .Y. .R.
GRB YGR BYG RBY GYB GRB
.R. YRR .Y. RRY .R. .Y.
Выходные данные
11
Входные данные
2
ZZ ZZ ZZ ZZ ZZ ZZ
ZZ ZZ ZZ ZZ ZZ ZZ
Выходные данные
8
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест