Темы --> Информатика --> Алгоритмы --> Вычислительная геометрия
    Градиентный спуск(1 задач)
    Элементарная геометрия(144 задач)
    Многоугольники. Выпуклые оболочки(38 задач)
    Клеточная геометрия(8 задач)
    Квадродерево(3 задач)
---> 9 задач <---
Источники --> Личные олимпиады --> Московская олимпиада школьников
    6-9 классы(30 задач)
    7-9 классы(25 задач)
    10-11 классы(114 задач)
Страница: 1 2 >> Отображать по:
#488
Найди прямую
  

Максимальное время работы на одном тесте:

2 секунды

Максимальный объем используемой памяти:

64 мегабайта

На плоскости дано множество отрезков. Требуется найти прямую, которая пересекла бы наибольшее возможное количество из данных отрезков и при этом проходила бы как минимум через две точки с целочисленными координатами.

Считается, что прямая пересекает отрезок, если она имеет с ним хотя бы одну общую точку (т.е. она может проходить через конец отрезка, внутреннюю точку отрезка, либо содержать весь отрезок).

Формат входных данных

Сначала вводится число N — количество отрезков (1≤N≤1000). Далее идет N четверок чисел Xi1, Yi1, Xi2, Yi2 задающих координаты концов отрезков. Все эти числа целые, по модулю не превосходящие 10000.

Заданные отрезки могут пересекаться, иметь общие части, один из них может полностью содержаться внутри другого. Отрезки имеют ненулевую длину.

Формат выходных данных

Выведите координаты каких-нибудь двух точек, через которые проходит прямая, пересекающая наибольшее количество отрезков. Координаты точек должны быть целыми и не должны по модулю превышать 107.

Примеры

Входные данные

Выходные данные

Пояснение

(кол-во отрезков, пересекаемых прямой)

3
0 0 1 0
0 1 1 1
0 2 1 2

0 -1 1 4

3

2
0 0 1 0
0 0 1 0

0 0 1 0

2

2
0 0 1 0
2 0 1 0

1 0 1 1

2

5
-1 0 3 4
2 3 5 6
0 2 2 -2
8 5 9 2
8 5 9 2

10 3 1 4

4
#493
Формула - 3
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Топологическая сортировка

В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.

1

Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.

Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).

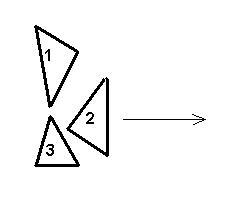
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).

Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).

Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.

Входные данные

В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).

В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.

Выходные данные

Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.

Примечание: первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным

Примеры
Входные данные
3
1 19 3 9 6 15
5 6 10 2 10 12
1 1 6 1 3 7
Выходные данные
Входные данные
3
0 1 -2 1 -1 -1
5 6 10 2 10 12
1 1 6 1 3 7


Выходные данные

                            
                                


                        

                    

                    

                        

                            

                                #496
                            

                            

                                Точки
                            

                              
                
                            

                                
                                
                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        2.0 second;
                                    
                                        
ограничение по памяти на тест

                                        64 megabytes
                                    

                                

                            
                            

   




Петя и Вася играют в "точки". Петя отметил на клетчатом листе бумаги несколько точек – узлов сетки. Вася хочет окружить их многоугольником так, чтобы все отмеченные узлы лежали строго внутри (не на границе) этого многоугольника и чтобы все стороны этого многоугольника проходили только по сторонам или диагоналям клеток сетки, а его периметр был минимально возможным. Определите, чему равен периметр такого многоугольника.


   


   

    

     Входные данные
    




В первой строке входных данных содержится число N – количество отмеченных Петей точек (1 ≤ N ≤ 100 000). 



В каждой из следующих N строк записаны по два числа xi, yi – координаты точек, нарисованных Петей. Координаты по абсолютной величине не превосходят 106. Некоторые точки могут совпадать.


   


   

    

     Выходные данные
    




Требуется вывести одно число – периметр искомого многоугольника. Ответ нужно вывести с точностью не менее 0.001.



    

    



                            
Примеры
Входные данные
1
0 0

Выходные данные
5.6568542495

Входные данные
2
1 1
1 2

Выходные данные
7.6568542495


                            
                                


                        

                    

                    

                        

                            

                                #513
                            

                            

                                Шахматная доска
                            

                              
                
                            

                                
                                
                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        1.0 second;
                                    
                                        
ограничение по памяти на тест

                                        64 megabytes
                                    

                                

                            
                            

   

    

		Из шахматной доски по границам клеток выпилили связную (не распадающуюся на части) фигуру без дыр. Требуется определить ее периметр.
    

   


   

    

     Входные данные
    

    

		Сначала вводится число \(N\) (1 ≤ \(N\) ≤ 64) – количество выпиленных клеток. В следующих \(N\) строках вводятся координаты выпиленных клеток, разделенные пробелом (номер строки и столбца – числа от 1 до 8). Каждая выпиленная клетка указывается один раз.
    

   


   

    

     Выходные данные
    

    

		Выведите одно число – периметр выпиленной фигуры (сторона клетки равна единице).
    


   

 

    

     Пояснения к примерам
    

    

1) Вырезан уголок из трех клеток. Сумма длин его сторон равна 8. 


2) Вырезана одна клетка. Ее периметр равен 4.
    


   



                            
Примеры
Входные данные
3
1 1
1 2
2 1

Выходные данные
8

Входные данные
1
8 8

Выходные данные
4


                            
                                


                        

                    

                    

                        

                            

                                #594
                            

                            

                                Восстанови многоугольник
                            

                              
                
                            

                                
                                
                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        1.0 second;
                                    
                                        
ограничение по памяти на тест

                                        64 megabytes
                                    

                                

                            
                            

   

    

		Вася нарисовал на клетчатой бумаге многоугольник, все стороны которого проходят по линиям сетки. После этого в каждой клетке он написал число, равное количеству сторон данной клетки, которые принадлежат сторонам многоугольника. Затем он стер многоугольник так, что остался листок бумаги, в каждой клетке которого написано число.



Восстановите нарисованный Васей многоугольник.
    

   


   

    

     Входные данные
    

    
В первой строке входных данных содержатся два натуральных числа: \(Y\) - количество строк и \(X\) - количество столбцов листа (3 <= \(Y\) <= 1000, 3 <= \(X\) <= 1000). В каждой из следующих \(Y\) строк задается по \(X\) целых неотрицательных чисел, не превосходящих 4. Ни одна из сторон многоугольника не проходит по границе листа бумаги.
    

   


   

    

     Выходные данные
    

    

		Выведите искомый многоугольник в следующем формате.



Выходные данные должны содержать  \(Y\) строк по 2\(X\)-1 символов в каждой (по одному символу на клетку и линию между клетками).



В первой строке выведите вертикальные отрезки в верхнем ряду клеток, обозначая их символом | (вертикальная черта - символ с кодом 124) и горизонтальные отрезки, отделяющие первый ряд клеток от следующего, обозначая их символом _ (подчеркивание). Если соответствующий отрезок в данном многоугольнике отсутствует, выведите вместо него символ . (точка). Во второй строке выведите в том же формате вертикальные отрезки во втором ряду и горизонтальные отрезки, отделяющие второй ряд от третьего. И т.д. В каждой строке на нечетных местах могут стоять только символы точка или подчеркивание, на четных местах - символы точка или вертикальная черта.



Гарантируется, что хотя бы одно решение существует. Если решений несколько, выведите любое из них.
    


   

 

 

                            
Примеры
Входные данные
4 4
0 0 1 0
0 2 3 1
1 3 2 1
0 1 1 0

Выходные данные
...._..
.._|.|.
.|_._|.
.......


                            
                                


                        

                    

                

                
        

            Страница: 
                    1
                    2
                >>
            Отображать по:
            
        

    
            

        

        
    
    

    

        

            
Выбрано
:
            
Отменить
|
            
Добавить в контест