Темы --> Информатика --> Язык программирования
    Процедуры и функции(96 задач)
    Массивы(232 задач)
    Типы данных(356 задач)
    Циклы(177 задач)
    Условный оператор (if)(164 задач)
    Python(260 задач)
    Standard Template Library(2 задач)
---> 19 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников --> Муниципальный этап --> Москва
    2007(5 задач)
    2008(5 задач)
    2009(5 задач)
    2010(5 задач)
    2011(5 задач)
    2012(5 задач)
    2013(5 задач)
    2014(5 задач)
Страница: << 1 2 3 4 >> Отображать по:
#3016
Списывание
  
Темы: [Цикл for]

На контрольной работе N учеников сидят в ряд. Для каждого ученика известно, какую оценку он получил бы, если бы писал эту контрольную самостоятельно (оценка — это число от 2 до 5). Однако ученики могут писать контрольную не только самостоятельно, но и списывать у своего соседа, но только если сосед пишет контрольную самостоятельно. В этом случае списывающий получит такую же оценку, какую получит тот, у кого он списал.

А именно (правила применяются строго в указанном порядке):

  • Школьники, которые знают материал на 5, будут писать контрольную самостоятельно.
  • Школьник, который знает материал на 4, если он сидит рядом с тем, кто знает на 5, будет списывать у него, а в противном случае будет писать самостоятельно.
  • Школьник, который знает на 3, если он сидит рядом с тем, кто знает на 5, будет списывать у него. Если среди его соседей знающего на 5 нет, но есть тот, кто знает на 4, и при этом пишет самостоятельно, то троечник будет списывать у него. В противном случае будет писать самостоятельно.
  • Аналогично школьник, знающий на 2 — из соседей, которые пишут самостоятельно, выберет того, кто знает лучше, и спишет у него. А если таких нет (или оба его соседа также знают на 2), то будет писать самостоятельно.

Определите, кто какую оценку в итоге получит.

Входные данные

Вводится число N (1<=N<=10) - количество учеников, и далее последовательность из N чисел, описывающая, кто на какую оценку может написать контрольную, если будет писать самостоятельно.

Выходные данные

Выведите N чисел - оценки, которые получат ученики за контрольную.

Примечания к примерам тестов

1. Первый и пятый ученики будут писать самостоятельно. Второй спишет у первого, а четвертый — у пятого (в итоге также получат пятерки). Третьему не у кого списывать, так как его соседи будут писать работу не самостоятельно.

2. Второй и четвертый спишут у третьего, пятый — у шестого.

Примеры
Входные данные
5
5
2
3
4
5
Выходные данные
5
5
3
5
5
Входные данные
6
2
2
3
2
2
4
Выходные данные
2
3
3
3
4
4
#3017
Последовательности
  
Темы: [Цикл while]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Рассмотрим последовательности чисел. Первая последовательность состоит из одного числа K. Каждая следующая последовательность чисел описывает предыдущую по такому правилу.

Просматриваем описываемую последовательность слева направо и разбиваем на отрезки, состоящие из подряд идущих равных чисел (причем все идущие подряд одинаковые числа всегда объединяем в один отрезок). Далее каждый такой отрезок описываем двумя числами — первое число говорит, сколько раз повторяется одно и то же число, второе число говорит, какое именно число повторяется. Записываем эти пары последовательно в соответствии с отрезками слева направо, и получаем новую последовательность (см. примеры ниже).

Например, для K=2 последовательности получатся такими:

№ Последовательность Как ее читать (слова в описании соответствуют числам текущей последовательности слева направо, и описывают предыдущую последовательность)
1 2 Исходная последовательность
2 1 2 Одна «двойка»
3 1 1 1 2 Одна «единица», одна «двойка»
4 3 1 1 2 Три «единицы», одна «двойка»
5 1 3 2 1 1 2 Одна «тройка», две «единицы», одна «двойка»
6 1 1 1 3 1 2 2 1 1 2 Одна «единица», одна «тройка», одна «двойка», две «единицы», одна «двойка»

Напишите программу, которая по исходному числу K напечатает N-ую получающуюся последовательность.

Входные данные

Вводится число K (1 ≤ K ≤ 9) и число N (1 ≤ N ≤ 15).

Выходные данные

Ваша программа должна печатать N-ую последовательность, полученную из начальной последовательности, состоящей из одного числа K. Числа при выводе следует разделять пробелами.

Примеры
Входные данные
2
6
Выходные данные
1 1 1 3 1 2 2 1 1 2
Входные данные
2
1
Выходные данные
2
Входные данные
1
3
Выходные данные
2 1
#3018
Сравнения
  

Про три числа (обозначенных a, b, c) известны все результаты сравнения их друг с другом. Требуется расположить эти числа в порядке возрастания.

Входные данные

Вводятся три строки. В первой записан результат сравнения между собой чисел a и b в следующем формате. Первый символ — всегда a, третий символ — b (соответствующие маленькие латинские буквы), а между ними записан один из символов >, < или =. Во второй строке в таком же формате записан результат сравнения a и с (первый символ всегда a, третий — c), а в третьей строке — результат сравнения b и c (первый символ всегда b, третий — c). Гарантируется, что входные данные не противоречивы.

Выходные данные

Выведите символы a, b, c в порядке величины соответствующих им чисел — каждое следующее число должно быть больше либо равно предыдущему. Если два числа равны между собой, соответствующие переменные могут быть выведены в любом порядке. Символы должны быть выведены в одной строке без пробелов и других разделителей.

Примечание

Во втором примере ответ cba также является верным. Обратите внимание, если вариантов ответа несколько — не нужно выводить их все, ваша программа должна вывести ровно один вариант ответа.

Примеры
Входные данные
a>b
a>c
b>c
Выходные данные
cba
Входные данные
a=b
a>c
b>c
Выходные данные
cab
cba
#3816
Замок
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

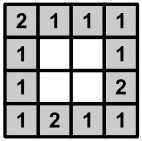
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.

Входные данные

Первая строка входных данных содержит число N — размер замка (2 ≤ N ≤ 100). Вторая строка входных данных содержит число K — количество полков, охраняющих замок (0 ≤ K ≤ 100).

Выходные данные

Выведите единственное число — количество полков на наименее укрепленной стороне замка при наилучшем размещении полков. Если имеющихся полков недостаточно для защиты всех башен, выведите число 0.

Примеры тестов

Входные данные
2
5
Выходные данные
2
Входные данные
4
15
Выходные данные
5

Примечание

В первом примере башни четыре, а полков пять, поэтому на одну из башен можно поставить два полка, но все равно найдется сторона, которую защищает всего два полка.

Во втором примере можно расположить полки так, что каждую сторону будет защищать 5 полков. Защитить каждую сторону не менее, чем шестью полками не удастся.

#111854
Пирожные
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Для праздничного чаепития необходимо купить \(n\) пирожных. В магазине продается всего два вида пирожных, причем пирожных одного вида осталось \(a\) штук, а пирожных другого вида осталось \(b\) штук. Пирожные одного вида считаются одинаковыми. Сколькими способами можно купить ровно \(n\) пирожных?

Входные данные

В первой строке входных данных записано число \(n\) — количество пирожных, которое нужно купить, во второй и третьей строке записаны числа \(a\) и \(b\) — количество пирожных каждого из двух видов, которые есть в магазине. Все числа — целые, от 1 до 100.

Выходные данные

Программа должна вывести одно целое число — количество различных способов купить \(n\) пирожных.

Примечание

В примере из условия купить 5 пирожных можно 4 способами: 0 пирожных первого вида и 5 пирожных второго вида, 1 пирожное первого вида и 4 пирожных второго вида, 2 пирожных первого вида и 3 пирожных второго вида, 3 пирожных первого вида и 2 пирожное второго вида. Больше способов нет, так как в магазине есть только 3 пирожных первого вида.

Примеры
Входные данные
5
3
10
Выходные данные
4
Страница: << 1 2 3 4 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест