#3295

Параллелограмм (10-11)

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача C ]

На уроке геометрии семиклассники Вася и Петя узнали, что такое параллелограмм. На перемене после урока они стали играть в игру: Петя называл координаты четырех точек в произвольном порядке, а Вася должен был ответить, являются ли эти точки вершинами параллелограмма.

Вася, если честно, не очень понял тему про параллелограммы, и ему требуется программа, умеющая правильно отвечать на Петины вопросы.

Напомним, что параллелограммом называется невырожденный четырехугольник, противоположные стороны которого параллельны.

Входные данные

В первой строке входного файла записано целое число \(N\) (\(1 \leq N \leq 10\)) - количество заданных Петей вопросов. Каждая из \(N\) последующих строк содержит описание четырех точек - четыре пары целых чисел \(X\) и \(Y\) (\(-100 \leq X\leq 100\), \(-100\leq Y \leq 100\)), обозначающих координаты точки.

Выходные данные

Для каждого из вопросов определите, образуют ли данные точки параллелограмм. Если они образуют параллелограмм, то выведите номера этих точек в одной строке через пробел в порядке обхода параллелограмма. Начинать обход можно с любой из вершин. Если они не образуют параллелограмм, выведите в этой строке одно число 0. Ответ на каждый из запросов должен быть в отдельной строке.

Примеры

Входные данные

3
1 1 4 2 3 0 2 3
1 1 5 2 2 3 3 0
0 0 5 1 6 3 1 2

Выходные данные

1 3 2 4
0
1 2 3 4

#3297

Поход (10-11)

Темы: [Динамическое программирование: один параметр]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача D ]

Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.

Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.

Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.

Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.

Входные данные

Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(10^5\) символов.

Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.

Выходные данные

Выведите одно целое число - минимальное количество переправ.

Примечания

Рисунок к приведенному выше примеру.

Примеры

Входные данные

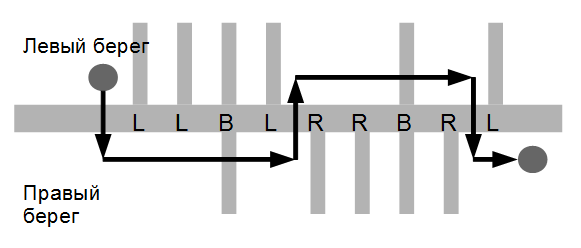
LLBLRRBRL

Выходные данные

#3298

Футурама

Источники: [ Личные олимпиады, Московская олимпиада школьников, 6-9 классы, 2011, Задача E ] [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2011, Задача E ]

С помощью изобретенной профессором машины Фарнсворт и Эми меняются телами с целью осуществить свои мечты: профессор жаждет острых ощущений, а Эми мечтает есть от пуза, не опасаясь за фигуру. Впоследствии выясняется, что обмен разумом между двумя телами возможен не более одного раза, и чтобы вернуться обратно в свои тела нужно произвести промежуточный обмен. Бендер предлагает свою помощь, однако, заполучив тело Эми, он тут же скрывается, чтобы под чужой личиной украсть корону императора Робо-Венгрии.
Эми, недовольная возможностями профессорского тела в плане обжорства, уговаривает поменяться Лилу. Фрай приходит в ужас. Лила обижена и обвиняет Фрая в том, что его заботит только ее внешность. Фрай в отместку меняется телами с Зойдбергом.
Бендер оказывается пойман при попытке ограбления, однако освобождается, убедив императора в том, что он - робот в теле человека. Узнав, что император втайне мечтает пожить немного жизнью простых людей, Бендер предлагает тому на время поменяться телами. Но так как Профессор уехал рисковать жизнью в теле Бендера, пришлось подсунуть императору вместо своего корпуса автоматизированное помойное ведро.
Фрай в теле Зойдберга и Лила в теле Профессора встречаются в ресторане, чтобы выяснить отношения. В конце концов они понимают, что любят друг друга вовсе не за внешность. При виде сцены их бурного примирения Эми, на этот раз уже в теле Гермеса, надолго теряет аппетит.
Бендер, поменявшись телами с правителем Робо-Венгрии, наслаждается жизнью на его яхте. Однако именно в этот вечер заговорщики совершают покушение на императора. Жизнь Бендеру спасает появление профессора Фарнсворта.
После того, как все герои решают свои личные проблемы, профессору с помощью Бубльгума Тэйта и Сладкого Клайда из команды "Ударники" удается вернуть всех в свои тела.

"Футурама". Десятый эпизод шестого сезона.

В очередной серии Футурамы было проведено несколько обменов разумами между телами героев,но, по крайней мере Бубльгум Тэйт и Сладкий Клайд в обменах не участвовали. Теперь необходимо вернутьразумы всех героев в свои тела. К сожалению, два тела могут участвовать только в одном обмене,поэтому обратные обмены для этого произвести невозможно. Например, если тело 1поменялось разумом с телом 2, а потом тело 1 поменялось разумом с телом 3,то в теле 1 находится разум третьего героя, в теле 2 - разум первого героя,а в теле 3 - второго.Теперь можно произвести обмен разумами только между телами 2 и 3, тогда разум второго героявернется в свое тело, а первому и третьему героям могут помочь только Тэйт с Клайдом.

Помогите героям Футурамы вернуться в свои тела.

Входные данные

Во входном файле записаны целые числа \(N\) (\(4\leq N\leq 20\)) и \(M\)(\(1\leq M\leq 100\)) - количество героев Футурамы и количество произведенных обменов разумами.Герои занумерованы числами от \(1\) до \(N\), изначально разум каждого из героев находится в своем теле. В последующих \(M\) строчках записана последовательность совершенных обменов разумами. Каждый обмен описывается двумя различными числами - номерами тел, которые, в этом обмене меняются разумами. Бубльгум Тэйт и Сладкий Клайд, как наиболее разумные герои, имеют номера \(N-1\) и \(N\), и гарантируется, что в исходных обменах они не участвовали.

Решения, верно работающие в случаях, когда каждое тело участвовало в обмене не больше одного раза будут набирать не менее 40 баллов.

Выходные данные

Выведите план обменов для возвращения разумов героев в свои телав виде пар различных чисел - номеров тел которые участвовали в соответствующем обмене.Причем никакие два тела не должны обмениваться между собой разумами более одного раза,включая исходные обмены. Если обменов не требуется, то можно ничего не выводить.Если планов обменов несколько, то выведите любой из них (не обязательно минимальный).

Вернуть разумы героев в свои тела всегда возможно.

Примечание

Приведем таблицу положения героев в телах после каждого из обменов:

Обмен	Тело 1	Тело 2	Тело 3	Тело 4
До обменов	1	2	3	4
1-2	2	1	3	4
1-3	3	1	2	4
2-4	3	4	2	1
1-4	1	4	2	3
2-3	1	2	4	3
3-4	1	2	3	4

Примеры

Входные данные

4 1
1 2

Выходные данные

#112044

Предложения с большой буквы, тест 1

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2012, Предложения с большой буквы, тест 1 ] [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2012, Задача A ]

Условие пока не опубликовано...

#112045

Предложения с большой буквы, тест 2

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2012, Задача B ]

Условие пока не опубликовано...