Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
Сегодня Игорь получил долгожданное разрешение на проведение эксперимента по изучению протекания химических реакций в магнитном поле. При этом используются две установки – генератор магнитного поля и манипулятор, соединяющий реагенты.
Эксперимент разбит на некоторое количество этапов, при этом некоторые из них могут быть выполнены только после завершения определенного набора других этапов. Правда известно, что хотя бы один способ проведения эксперимента существует. На каждом этапе Игорь должен управлять ровно одной из двух установок – либо генератором, либо манипулятором.
Игорь очень дорожит своим временем, и поэтому он хочет провести эксперимент, совершив наименьшее количество перемещений между пультами управления установками. Помогите ему узнать, в каком порядке следует выполнять этапы, чтобы этого добиться.
В первой строке вводится целое число n – количество этапов эксперимента ( 1![]() n
n![]() 100).
100).
Следующие n строк содержат описание этапов. Пронумеруем этапы от 1 до n в некотором произвольном порядке. Тогда i-я из этих строк описывает i-й этап. Каждый этап описывается последовательностью целых чисел. Первое число равно нулю, если на этом этапе Игорь управляет генератором, и единице, если он управляет манипулятором. Затем записано целое число ri – количество этапов, которые должны быть выполнены перед выполнением данного. За ним следуют номера этих этапов – ri различных целых чисел в диапазоне от 1 до i - 1.
В первой строке выведите минимальное количество перемещений, которые придется совершить Игорю. Во второй строке выведите перестановку чисел от 1 до n – последовательность, в которой следует выполнять этапы. Если решений несколько, выведите любое.
3 1 0 0 0 1 2 1 2
1 2 1 3
Во Флатландии n городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание n - 1 шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды – числа от 1 до n.
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача – таким образом сопоставить числам от 1 до n города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
В первой строке вводится целое число n – количество городов во Флатландии ( 2![]() n
n![]() 1500).
1500).
Далее следует n описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города – строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа x и y – координаты города. Координаты не превышают 104 по абсолютной величине.
Далее следуют n - 1 строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа – номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более, чем одним шоссе.
Выведите n строк, i-я из этих строк должна содержать название города, который следует сопоставить числу i в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите строку «No solution».
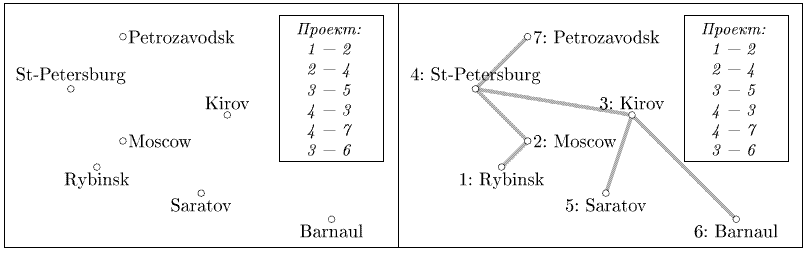
7 Moscow 2 2 St-Petersburg 0 4 Kirov 6 3 Saratov 5 0 Rybinsk 1 1 Petrozavodsk 2 6 Barnaul 10 -1 1 2 2 4 3 5 4 3 4 7 3 6
St-Petersburg Rybinsk Kirov Saratov Moscow Petrozavodsk Barnaul
При расследовании дорожно-транспортных происшествий часто возникают проблемы с розыском автомобилей, водители которых покинули место происшествия.
Получение свидетельских показаний – непростая работа. Ситуация осложняется тем, что очень часто свидетели могут только приблизительно вспомнить номер автомобиля. При этом с большой вероятностью опрашиваемый может перепутать порядок цифр или букв в номере.
По полученному от свидетеля происшествия номеру, подсчитайте, сколько различных номеров может получиться из него перестановкой букв и/или цифр, а также выведите все такие номера.
Напомним, что автомобильные номера в России состоят из трех букв и трех цифр, упорядоченных следующим образом: буква, три цифры, затем две буквы. Фрагмент номера, который идентифицирует регион, в котором зарегистрирован автомобиль, мы будем игнорировать.
В номере могут использоваться следующие буквы: «A», «B», «C», «E», «H», «K», «M», «O», «P», «T», «X», «Y» (эти буквы имеют схожие по написанию аналоги как в русском, так и в латинском алфавите). В этой задаче во входных данных будут использоваться буквы латинского алфавита.
На вход программы поступает одна строка, которая представляет собой корректный автомобильный номер.
В первой строке выведите число k – количество номеров, которые могут получиться из заданного перестановкой букв и/или цифр.
В последующих k строках выведите все такие номера в произвольном порядке.
X772KX
9 X277XK X277KX X727XK X727KX X772XK X772KX K277XX K727XX K772XX
На планете Плюк, поверхность которой мы будем считать абсолютно плоской, был разработан новый принцип перемещения единственного имеющегося там транспортного средства – пепелаца. А именно, на расстоянии одного километра друг от друга в точках (0, 0) и (1, 0) были построены две станции управления пепелацами A и B. С помощью них можно мгновенно переместить любой пепелац, повернув его на 90 градусов по или против часовой стрелки относительно точки A или B. Расстояние от пепелаца до соответствующей станции при этом не меняется. Следующее перемещение можно делать как относительно той же станции, так и относительно другой.
Например, если повернуть пепелац, находящийся в точке (3, 1) на 90 градусов против часовой стрелки относительно станции A, то он переместится в точку (- 1, 3), если его затем повернуть на 90 градусов по часовой стрелке относительно станции B, то он переместится в точку (4, 2), если затем повернуть его вокруг станции B по часовой стрелке еще раз, он переместиться в точку (3, - 3).
Один житель планеты недавно решил отправиться на своем пепелаце в гости к другу. Житель проживает около точки с координатами (x1, y1), а его друг – около точки с координатами (x2, y2). Помогите жителю с помощью станций управления пепелацем оказаться как можно ближе к месту, где проживает его друг, чтобы потом меньше было идти по пустыне.
Поскольку перемещения мгновенные и абсолютно бесплатные, то минимизировать количество перемещений не надо.
На вход программы поступают четыре целых числа – x1, y1, x2 и y2, они не превышают 104 по абсолютной величине.
Выведите последовательность перемещений с использованием станций управления, которая перемещает пепелац из точки (x1, y1) как можно ближе к точке (x2, y2).
Поворот по часовой стрелке относительно станции A обозначается как «+A», поворот против часовой стрелки относительно станции A обозначается как «-A», соответствующие повороты относительно станции B обозначаются как «+B» и «-B». Выводите по одному перемещению на строке.
Выведенная последовательность не обязана быть минимальной по количеству перемещений, но должна содержать не более 106 действий.
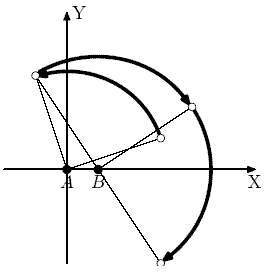
3 1 3 -3
+A -B -B +A +A -B -B +A
0 0 3 0
-A +B +A -B
Одной из первоочередных задач, стоящих перед министерством обороны Флатландии, является модернизация вооружения. В связи с этим было решено построить новый испытательный полигон.
По форме полигон представляет собой выпуклый многоугольник. Для демонстрации военных испытаний на полигоне различным чиновникам, неподалеку от него решено было построить наблюдательный центр. В результате длительных исследований было установлено, что основной характеристикой местоположения наблюдательного центра является степень этого центра относительно полигона.
Степень точки A относительно многоугольника вычисляется по следующему правилу. Рассмотрим все лучи с вершиной в точке A, имеющие общие точки с многоугольником. Для каждого такого луча найдем минимальное и максимальное расстояние вдоль него от точки A до некоторой точки многоугольника: dmin и dmax. Степенью точки относительно данного многоугольника назовем минимум величины dmin×dmax по всем таким лучам.
Военные не справляются с задачей вычисления степени наблюдательного центра относительно полигона и решили подключить к этой задаче вас. Помогите им!
Будем считать, что наблюдательный центр находится в точке (0, 0). На вход программы поступает описание полигона.
В первой строке вводится число n – количество вершин полигона ( 3![]() n
n![]() 100). Следующие n строк содержат по два вещественных числа – координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают 1000 по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
100). Следующие n строк содержат по два вещественных числа – координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают 1000 по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
Выведите одно число – степень наблюдательного центра относительно полигона. Ответ должен отличаться от правильного не более чем на 10-4.
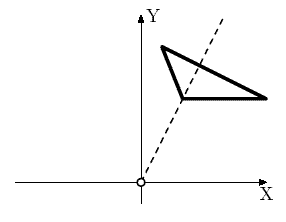
3 1.0 2.0 3.0 2.0 0.5 3.25
7.0000000000