Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
Вы никогда не задумывались, почему в Angry Birds у птиц нет крыльев? Тем же вопросом задались разработчики новой игры. В их версии смысл игры прямо противоположен Angry Birds: зеленая свинка стреляет по злым птицам из лазерного ружья (завязка явно не хуже исходной игры).
Птицы в игре представляются точками на плоскости. Выстрел сбивает только ближайшую птицу находящуюся на линии огня. При этом сбитая птица падая сбивает всех птиц, находящихся ровно под ней. Две птицы не могут находиться в одной точке. По заданному расположению птиц необходимо определить, какое минимальное количество выстрелов необходимо, чтобы все птицы были сбиты.
Первая строка входного файла содержит единственное целое число N 1 ≤ N ≤ 1000 — количество птиц.
Следующие N строк содержат по два натуральных числа каждая xi, yi — координаты i-ой птицы (0 < x, y ≤ 109). Свинка находится в точке с координатами (0, 0).
Единственная строка выходного файла должна содержать одно целое число — минимальное количество выстрелов, необходимое для того, чтобы сбить всех птиц.
6 1 1 2 2 3 3 2 1 3 2 3 1
3
6 1 1 2 2 3 3 2 1 3 2 3 4
3
Когда Петя учился в младших классах, он любил заниматься выпиливанием лобзиком из фанеры различных фигурок. Чтобы можно было заново выпилить наиболее интересные варианты, каждый раз делая распил, он записывал в свою тетрадку, какую фигуру он распилил на какие части.
Недавно Петя нашел у себя в тетрадке запись, из которой следовало, что он распилил n-угольник вдоль прямой, проходящей через две его вершины. В результате распила образовалось ровно две части, одна из которых — k-угольник, а другая — m-угольник. Петя заинтересовался, каким образом такое могло получиться.
Помогите Пете, постройте n-угольник и укажите в нем две различные вершины A и B таким образом, чтобы при распиле n-угольника вдоль прямой AB, получилось ровно два многоугольника, один из которых является k-угольником, а другой — m-угольником.
Входной файл содержит три целых числа: n, m и k (3 ≤ n, m, k ≤ 200).
Если описанная в условии ситуация могла иметь место, выведите на первой строке выходного файла слово «Yes». В этом случае затем следует вывести пример многоугольника и распила. Следующие n строк должны содержать по два целых числа — координаты вершин многоугольника в порядке обхода. Координаты не должны превышать 104 по модулю. Граница многоугольника не должна иметь самопересечений и самокасаний. Никакие три подряд идущие вершины многоугольника не должны лежать на одной прямой.
Будем считать вершины пронумерованными от 1 до n в порядке, в котором они выведены. Последняя строка должна содержать два числа: номера вершин, через которые был проведен распил.
Если описанная в условии ситуация невозможна, выведите на первой строка выходного файла слово «No».
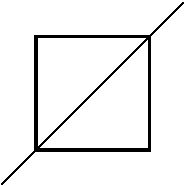
Рисунок ко второму примеру 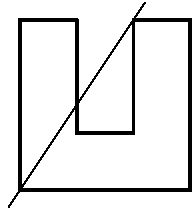
4 3 3
Yes 0 0 1 -4 1000 0 999 4 1 3
8 4 7
Yes 0 0 1 -4 1 -5 999 1 1000 0 999 4 999 5 998 4 1 5
В одной сельской школе решили начать преподавание информатики. Начали с создания кабинета информатики. Так как специального помещения для этих целей в школе нет, то было решено переоборудовать кабинет математики.
Было закуплено n устройств: системные блоки, мониторы, проектор и т. д. Однако, когда начался процесс подключения, неожиданно выяснилось, что в кабинете есть только одна электрическая розетка.
Решение было найдено достаточно быстро — были куплены k сетевых фильтров. После этого выяснилось, что как устройства, так и сетевые фильтры обладают различными характеристиками — это делает процесс подключения нетривиальным. Для каждого сетевого фильтра известно число Ai розеток в нем и максимальная суммарная мощность Bi устройств, которые могут быть в него подключены, а для каждого устройства известна потребляемая им мощность Ci.
Теперь необходимо составить схему подключения устройств с использованием сетевых фильтров такую, что суммарная мощность устройств, включенных в каждый сетевой фильтр (как напрямую, так и через другие сетевые фильтры) не превосходит соответствующего значения Bi, а число устройств и других сетевых фильтров, напрямую включенных в этот, не превосходит Ai. При этом, в соответствии с правилами пожарной безопасности, в каждый сетевой фильтр можно подключать не более одного другого сетевого фильтра.
Можно считать, что единственная в классе розетка рассчитана на достаточно большую мощность — она выдержит подключение всех имеющихся устройств. Отметим также, что при необходимости в розетку можно включить не сетевой фильтр, а устройство напрямую.
Напишите программу, которая найдет требуемую схему подключения устройств.
Первая строка входного файла содержит k — число имеющихся в наличии сетевых фильтров (1 ≤ k ≤ 100 000). Далее следуют k строк, описывающих эти сетевые фильтры: каждая из них содержит по два целых числа: Ai и Bi — количество розеток в нем и максимальную суммарную мощность приборов, которые можно включить в него, соответственно (2 ≤ Ai ≤ 100 000, 1 ≤ Bi ≤ 109).
Следующая строка содержит n — число приборов, которые нужно подключить (1 ≤ n ≤ 100 000). Последняя строка входного файла содержит мощности этих приборов: C1, ..., Cn (1 ≤ Ci ≤ 109).
В выходной файл выведите слово «Yes», если все приборы можно подключить с использованием имеющихся в наличии сетевых фильтров, и слово «No» — в противном случае.
Если ответ на задачу положительный, то далее выведите описание схемы подключения. Оно должно состоять из двух строк. Первая из этих строк должна описывать подключение сетевых фильтров: для каждого из них выведите номер фильтра, в который он подключен (если он подключен в единственную розетку в классе, то выведите число 0, а если он вообще не используется, то число - 1). Вторая из этих строк должна описывать подключение приборов: для каждого из приборов выведите номер сетевого фильтра (если прибор следует подключить непосредственно в розетку, то выведите число 0), в который он подключен.
Учитывайте, что в каждый сетевой фильтр может быть подключен не более чем один другой сетевой фильтр, а подключать фильтр сам к себе не разрешается. Если в сетевой фильтр не включены (напрямую или через другие сетевые фильтры) никакие устройства, то он также не должен быть никуда включен. Кроме этого, если фильтр не включен (напрямую или через другие сетевые фильтры) в розетку, то он также не должен быть никуда включен.
Сетевые фильтры нумеруются, начиная с единицы, в порядке их перечисления во входном файле. Порядок вывода описания подключения фильтров и приборов должен совпадать с порядком их перечисления во входном файле.
2 2 20 2 10 3 10 5 5
Yes 0 1 1 2 2
1 2 10 1 20
Yes -1 0
В деревне Гадюкино регулярно идут проливные дожди, в результате чего речка Вонючка, которую обычно можно просто перешагнуть, выходит из берегов. Чтобы можно было перейти разлившуюся реку, планируется построить плавучий мост из бревен, оставшихся от строительства бани бизнесмена, поселившегося неподалеку
Все оставшиеся бревна имеют одинаковую толщину. При этом есть \(x\) бревен длины \(a\) и \(y\) бревен длины \(b\)
Построенный мост должен состоять из \(l\) рядов, каждый из которых составлен из одного или нескольких бревен. Пилить бревна нельзя, так как последняя пила утонула при разливе Вонючки. Главный инженер хочет построить мост максимальной возможной ширины, при этом ширина моста определяется по минимальной ширине ряда бревен.
Например, если нужно построить мост из семи рядов, и при этом есть шесть бревен длины 3 и десять бревен длины 2, то можно построить мост ширины 5.
Входной файл содержит пять натуральных чисел: \(x\), \(a\), \(y\), \(b\) и \(l\). Все числа не превышают 150. Общее количество бревен не меньше \(l\).
Выведите в выходной файл одно число — максимальную возможную ширину моста
6 3 10 2 7
5
10 7 20 9 25
9
Летнее кафе имеет форму прямоугольника размером \(n\) × \(m\) клеток, в каждой из которых может находиться стол или стул
В кафе планируется проведение банкета на \(k\) персон. Для этого требуется расставить ровно \(k\) стульев так, чтобы рядом с каждым стулом (в одной из соседних клеток по вертикали, горизонтали или диагонали) был стол. Помогите администраторам кафе решить эту задачу или сообщите, что сделать это невозможно.
Входной файл содержит три числа \(n\), \(m\) и \(k\) (1 ≤ \(n\), \(m\) ≤ 50, 1 ≤ \(k\) ≤ 10000).
Выходной файл должен содержать n строк по m символов — план размещения столов и стульев для банкета. Символ «h» обозначает стул, символ «T» — стол, символ «.» — пустую клетку. Если решения нет, выведите строку «Impossible».
3 4 8
hhhh hThT hh..
2 2 4
Impossible