#111826

Странный город

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача H ]

В одной стране есть странный город. В этом городе есть $n$ перекрестков и $m$ улиц. Каждая улица соединяет ровно два различных перекрестка и по каждой улице можно двигаться в обоих направлениях.

Однажды с целью борьбы с пробками мэр города решил провести дорожную реформу. Он решил запретить автомобильное движение на некоторых улицах и сделать их пешеходными. При этом исследования департамента транспорта показали, что результаты реформы будут оптимальными, если после ее осуществления из каждого перекрестка будет выходить нечетное число улиц, на которых разрешено автомобильное движение.

Подчиненные мэра озадачены. Они никак не могут исполнить приказ мэра. Вам предлагается сделать это за них. Вам задана карта города, требуется решить, какие улицы необходимо сделать пешеходными, а какие - оставить для автомобилей, чтобы в результате реформы из каждого перекрестка выходило нечетное число улиц, по которым разрешено движение автомобилей.

Формат входного файла

В первой строке заданы целые числа $n$ и $m$ ($1 \le n \le 2 \cdot 10^5$, $0 \le m \le 2 \cdot 10^5$) - количество перекрестков и количество дорог в городе соответственно.

В следующих $m$ строках заданы дороги, каждая дорога описана в отдельной строке. В $(i+1)$-й строке описывается дорога с номером $i$. Каждая дорога задается двумя целыми числами $v$ и $u$ - номерами двух перекрестков, которые эта дорога соединяет ($1 \le v, u \le n$).

Гарантируется, что дорога не соединяет перекресток с самим собой.

Гарантируется, что любая пара перекрестков соединена не более чем одной дорогой.

Не гарантируется, что от исходно любого перекрестка можно добраться до любого другого по улицам.

Формат выходного файла

Если удовлетворить условие в приказе мэра невозможно, выведите единственное число $-1$ в первой строке выходного файла.

Иначе в первой строке выведите число $k$ - количество дорог, которые нужно оставить для автомобильного движения. В следующей строке выведите $k$ различных чисел через пробел - номера этих дорог. Дороги пронумерованы от 1 до $m$ в том порядке, в котором они заданы во входном файле.

Примеры

Входные данные

2 1
1 2

Выходные данные

1
1

Входные данные

Выходные данные

2
2 4

#111827

Длинный питон

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача I ]

Раз, два, левой, правой
дважды два - очень просто
измеряются удавы
пятью пять - любого роста

Попугай

После того, как Мартышка и Попугай досконально исследовали длину Удава, им стало очень скучно. Тут Слоненок вспомнил, что в лесу живет еще Питон, которого тоже можно измерять! Друзья сразу же отправились на его поиски.

Питон, как и Удав, тоже целый, поэтому его нельзя мерить половинками. Измерив Питона, Мартышка и Попугай узнали, что в Питоне помещается $n$ целых Попугаев или $m$ целых Мартышек. Обрадованная Мартышка убежала сообщить полученный результат Слоненку. Когда она ушла, Попугая заинтересовал следующий вопрос: а сколько раз он помещается в одной Мартышке?

Так как Мартышка убежала, и измерить ее он не может, Попугай решил попытаться выяснить, сколько целых Попугаев может поместиться в одной Мартышку, используя результаты измерения Питона. По заданным $n$ и $m$ выясните, какое минимальное и максимальное число целых Попугаев может помещаться в одной Мартышке.

Формат входного файла

Во входном файле заданы два целых числа $n$ и $m$, каждое на своей строке - количество Попугаев и Мартышек в Питоне, соответственно
($1 \le n, m \le 10^9$).

Формат выходного файла

В выходной файл выведите два числа - минимальное и максимальное количество целых Попугаев в одной Мартышке.

Примеры

Входные данные

38
5

Выходные данные

6
7

#111828

Швабра

Темы: [Вычислительная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача J ]

Первокурсник Рома приехал в общежитие и, удивившись беспорядку в комнате и толстому слою пыли на полу, начал наводить порядок. Первым делом он решил вымыть пол. Для этого Рома в магазине приобрел инновационную швабру.

Изначально моющая часть швабры имела идеальную прямоугольную форму, но в процессе перевозки из магазина в общежитие у нее отломился один из углов. Таким образом, теперь она представляет собой многоугольник, граница которого состоит из двух соседних сторон прямоугольника, фрагментов двух оставшихся сторон и ломаной, соединяющей концы этих фрагментов.

$\text{[math]}$

Рома живет в большой прямоугольной комнате. Рома провел сломанной шваброй от одной стороны комнаты до другой, не отрывая ее от стены, так что в результате отломанный угол швабры оказался в углу комнаты. При этом часть соответствующей прямоугольной полосы пола в углу осталась невымытой.

$\text{[math]}$

Рома считает, что все точки, в которых в какой-то момент находилась моющая часть швабры оказались вымыты. Теперь он решил выяснить, какая часть этой полосы осталась грязной.

$\text{[math]}$

Помогите ему вычислить площадь этой части. Можете считать, что размер комнаты, в которой живет Рома, существенно больше размеров моющей части швабры.

Формат входного файла

Первая строка входного файла содержит два целых числа $w$ и $h$ - размеры моющей части швабры до повреждения ($2 \le w, h \le 10^5$).

Вторая строка содержит целое число $n$ - число вершин ломаной, соединяющей соседние стороны швабры ($2 \le n \le 10^5$). В $i$-й из следующих $n$ строк заданы два целых числа $x_i$ и $y_i$ ($1 \le x_i < w$, $1 \le y_i < h$, за исключением $y_1 = h$, $x_n = w$) - координаты $i$-й вершины ломаной. Ломаная не имеет самопересечений и самокасаний.

Координаты введены таким образом, что стена, вдоль которой Рома провел шваброй, соответствует прямой $y=h$.

Формат выходного файла

В выходной файл выведите площадь невымытой части пола с абсолютной или относительной погрешностью не более $10^{-6}$. Это значит, что если правильный ответ $a$, а вы вывели $p$, то ваш ответ будет засчитан как правильный, если $\frac{|a-p|}{\max(|a|, 1)}\le 10^{-6}$.

Примеры

Входные данные

Выходные данные

18.0

#111829

Вампирские числа

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача K ]

Илья увлекается математикой. Недавно он прочитал про вампирские числа. Они настолько восхитили Илью, что теперь он постоянно придумывает задачи, связанные с этими числами, и пытается их решить.

Число $a$, десятичная запись которого состоит из $n$ цифр ($n$ четно), называется вампирским, если его можно представить в виде произведения двух
$n/2$-значных чисел $b$ и $c$, причем используя все цифры $b$ и $c$ можно записать число $a$. Каждую цифру при этом разрешается использовать столько раз, сколько раз она суммарно встречается в $b$ и в $c$. Числа $b$ и $c$ называются клыками числа $a$.

Например, число $6880$ - вампирское, так как $6880 = 80 \times 86$, а число $1023$ - нет.

Для его новой задачи Илья попросил вас найти $k$ различных вампирских чисел, состоящих из $n$ цифр.

Формат входного файла

В единственной строке входного даны два числа $k$ и $n$ - требуемое количество вампирских чисел и количество цифр в каждом из них соответственно ($1 \le k \le 100$, $4 \le n \le 100$, $n$ - четно).

Формат выходного файла

В выходной файл выведите $k$ различных $n$-значных вампирских числа в формате $A_i$=$B_{i}$x$C_{i}$, где $A_i$ - $i$-е из найденных вампирских чисел, $B_i$ и $C_i$ - его клыки (между $B_i$ и $C_i$ следует вывести маленькую латинскую букву «x»).

Если ответов несколько, то разрешается вывести любой из них. Гарантируется, что для приведенных во входном файле $n$ и $k$ существует $k$ различных $n$-значных вампирских чисел.

Примеры

Входные данные

1 6

Выходные данные

139500=150x930

#111842

Подсчёт столбов

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2013, Лига А, Задача A ]

Будущие программисты Андрей и Борис вчера впервые поехали кататься с родителями по новой кольцевой дороге. Каждый из них выехал на дорогу в определённом месте, сделал полный круг и вернулся домой. От скуки они оба считали фонарные столбы, расположенные посередине дороги между встречными полосами движения, так что все N фонарных столбов у каждого из мальчиков получили номера от 1 до N . Но само значение N они не запомнили. При этом два столба обоим мальчикам запомнились особенно: на одном из них висел яркий плакат ко Дню города, а на другом — флаг Москвы. Каждый из мальчиков записал себе в тетрадку номер каждого из этих двух столбов.

Сегодня обе семьи, Андрея и Бориса, пошли на выставку кошек, и там мальчики, обсудив свои поездки, задались вопросом: сколько же всего фонарных столбов на новой кольцевой дороге? Единственное, что они смогли выяснить, в одном ли направлении ехали они по дороге.

Так сложилось, что Андрей — ваш младший брат, поэтому именно вам предстоит ответить на вопрос мальчиков. У вас есть серьёзное подозрение, что может не получиться однозначно найти ответ, а мальчики боятся больших чисел, поэтому вы решили сказать им лишь минимальное из возможных значений числа N .

$\text{[math]}$

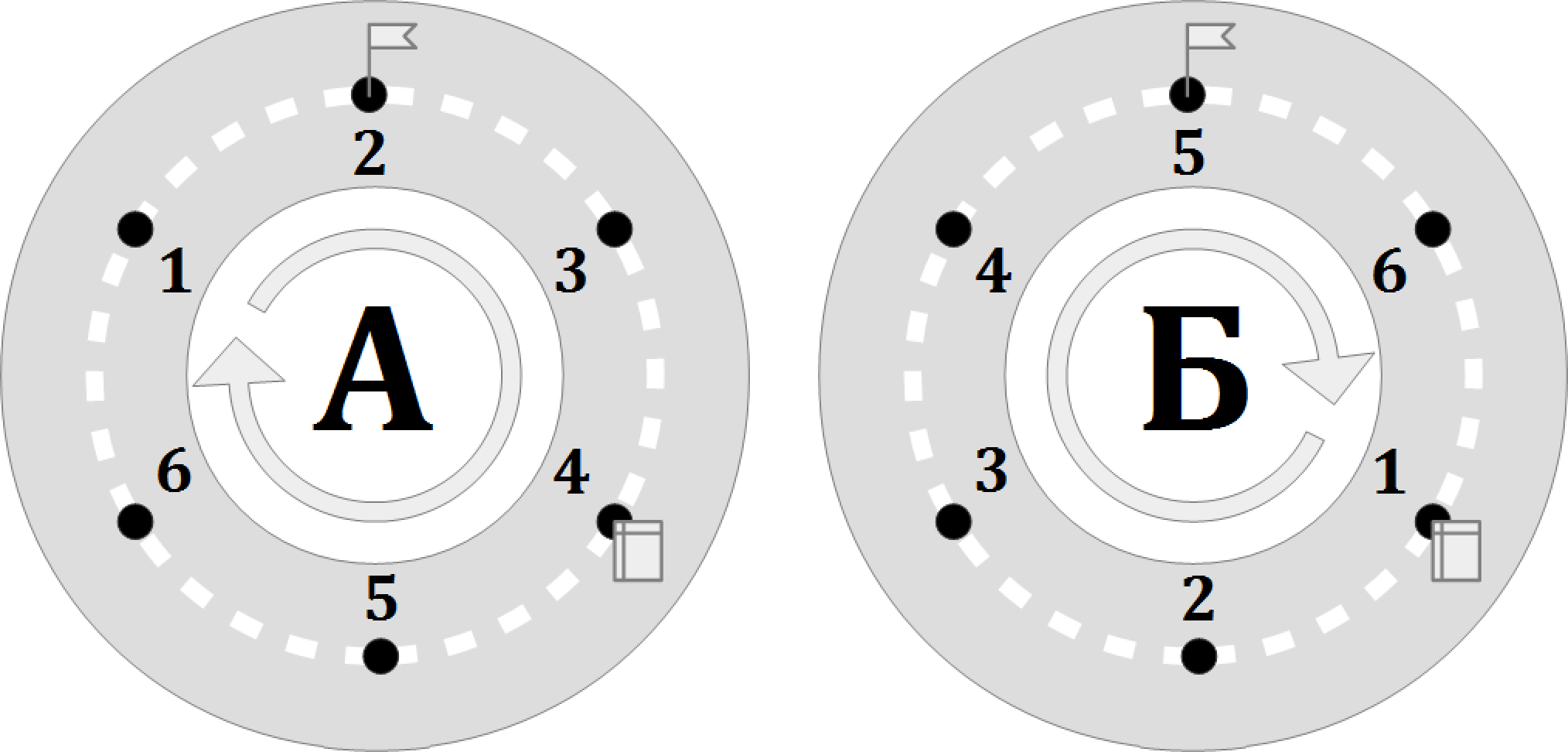
В этом примере N = 6 , A _p = 4 , A _f = 2 , B _p = 1 , B _f = 5 .

Входные данные

Первая строка входного файла содержит единственное целое число D , которое равно 1 , если мальчики ехали в одном направлении, и - 1 , если в разных. Вторая строка содержит 4 натуральных числа A _p , B _p , A _f , B _f , каждое из которых не превосходит 10 ⁹ : A _p — номер столба с плакатом в нумерации Андрея, B _p — номер этого столба в нумерации Бориса, A _f — номер столба с флагом в нумерации Андрея, B _f — номер этого столба в нумерации Бориса. Соседние числа в строке разделены одним пробелом. Плакат и флаг могли оказаться на одном столбе — в этом случае каждый из мальчиков должен был бы получить два одинаковых числа, т. е. A _p = A _f и B _p = B _f .

Выходные данные

Выведите единственное натуральное число N — минимально возможное количество столбов. Если мальчики где-то ошиблись, и таких чисел, как у них, не могло получиться ни при каком зна-че-нии N , выведите число - 1 .

Примеры

Входные данные

1
4 1 2 5

Выходные данные

Входные данные

-1
4 9 4 7

Выходные данные

-1