Вася очень любит различные игры: шашки, шахматы, домино, крестики-нолики и т. д. Поскольку он играет в них уже достаточно давно, он успел изучить эти игры достаточно хорошо, и они стали скучными. Поэтому он теперь изобретает новые игры на основе тех, в которые уже наигрался. Недавно он изобрел игру «Доминошахматы».
Она состоит в следующем: Вася берет у дедушки большой кусок фанеры и раскрашивает его так, что у него получается шахматная доска размера N × M клеточек. Потом он берет кости домино и пытается покрыть ими полученную доску так, чтобы все клеточки были закрыты, не было наложений и никакие доминошки не торчали за края доски (каждая доминошка покрывает две соседние клетки).
Поскольку Вася не спрашивает разрешения у дедушки прежде, чем взять доску, он иногда берет ненужные доски, а иногда и те, которые дедушка хотел использовать в строительстве новой дачи. Как раз сегодня Вася взял «нужную» доску, поэтому дедушка был вынужден вырезать из Васиной доски два квадрата по одной клеточке.
Вася сначала огорчился, что не сможет поиграть в свою игру. А потом решил попробовать замостить доску с уже вырезанными клетками, причем так, чтобы вырезанные клетки не были накрыты доминошками.
Помогите Васе понять, можно ли это сделать.
Выходные данные
Выведите «YES», если доску с вырезанными клеточками можно покрыть доминошками, и «NO» в противном случае. (Запас доминошек у Васи бесконечный.)
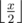 клеток до стены (
клеток до стены (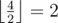 ,
, 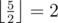 ).
).