Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
На соревнованиях по прыжкам на лыжах с трамплина техника прыжка оценивается пятью судьями. Каждый судья ставит оценку от \(1\) до \(20\), после чего одна наименьшая и одна наибольшая оценки отбрасываются. Вам нужно написать программу, которая будет демонстрировать результаты прыжка для телетрансляции.
Она должна выводить пять оценок, которые поставили судьи, не меняя их порядка, а затем их сумму, и при этом брать в скобки те оценки, которые не учитываются при расчете суммы
На вход подается \(5\) натуральных чисел от \(1\) до \(20\), разделенных пробелом.
Выведите те же числа в том же порядке, взяв в скобки минимальное (а если их несколько – самое левое из них) и максимальное (а если их несколько – самое правое из них) число, а также сумму всех чисел, не взятых в скобки. Все числа (включая сумму) должны быть напечатаны в одной строке и разделены одним пробелом (внутри скобок пробелов быть не должно). Перед суммой должен стоять знак равенства, отделенный слева и справа одним пробелом. Порядок оценок должен быть такой же, как и во входных данных.
1 2 3 4 5
(1) 2 3 4 (5) = 9
10 11 10 11 10
(10) 11 10 (11) 10 = 31
Магическим квадратом называют таблицу, в которой записаны числа \(1, 2, 3, …\) по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной \((3\times 3, 5\times 5, …)\).
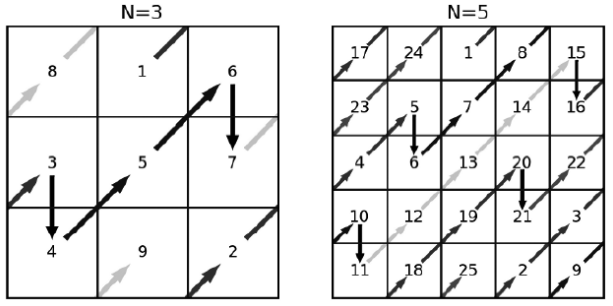
Поставим число \(1\) в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа \(2, 3, 4, …\). Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов \(3\times 3\) и \(5\times 5\) показаны на рисунках.
На вход подается одно натуральное нечетное число \(N\), не превосходящее \(30\) – размер квадрата.
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
3
8 1 6 3 5 7 4 9 2
5
17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9
Васе подарили два ежедневника на i-й год. Один он использовал в i-м году и теперь интересуется, когда наступит следующий год с точно таким же календарем, чтобы он мог воспользоваться вторым ежедневником.
Вводится одно натуральное число i, не превышающее 2011.
Выведите одно число - номер года, когда можно будет использовать второй ежедневник.
2011
2022
1
7
Как непросто быть школьником! Именно такие мысли чаще всего посещают Петю после уроков математики. Сегодня учительница рассказывала, что такое простые числа. Петя впервые услышал о них. Оказывается, простое число — это такое натуральное число, которое имеет ровно два различных натуральных делителя, то есть делится без остатка только на единицу и на само себя. После урока Петя и его друг Сережа придумали такую игру: один называет два числа A и B, а другой говорит, сколько нулей на конце произведения всех простых между A и B включительно. Петя заметил, что Сережа отвечает на вопрос намного быстрее, чем он сам, и очень просит вас ему помочь. Напишите для Пети программу, которая будет отвечать на вопросы Сережи.
На вход подается два числа A, B (1 ≤ A ≤ B ≤ 109), разделенных пробелом. Гарантируется, что между A и B есть хотя бы одно простое число.
Выведите количество нулей, на которое заканчивается произведение всех простых чисел на отрезке от A до B.
1 7
1
3 3
0
В одной маленькой стране разрешили открывать оффшорные компании, и туда тут же потянулись предприниматели с желанием открыть в ней свою фирму.
Поскольку все фирмы современные и идут в ногу со временем, им нужно связываться с клиентами и партнерами по бизнесу, а значит нужен и телефонный номер.
Таким образом, каждой букве соответствует некая цифра, и вместо телефонного номера достаточно знать слово, буквы которого соответствуют цифрам номера.
Каждая фирма хочет, чтобы ее телефонный номер было просто запомнить. Если набранное на телефоне название компании соответствует телефонному номеру компании, то номер очень легко запомнить, и ни один клиент его не забудет.
Поскольку фирм очень много, возможно, не все фирмы смогут получить удобный номер. Напишите программу, которая будет определять наибольшее количество фирм, которые смогут получить такой номер.
В первой строке вводится целое число N — количество новых фирм (1 ≤ N ≤ 103).
В последующих N строках вводятся названия фирм. Название каждой фирмы состоит из семи строчных латинских букв. Гарантируется, что названия всех фирм различны.
Выведите одно число — максимальное количество фирм, которые смогут получить удобный номер.
4 lacoste hyundai renault peugeot
4
3 aaaaaaa bbbbbbb ccccccc
1