Массивы(232 задач)
Типы данных(356 задач)
Циклы(177 задач)
Условный оператор (if)(164 задач)
Python(260 задач)
Standard Template Library(2 задач)
Дети решили поиграть в догонялки, и, чтобы выбрать водящего, встали в круг и стали считаться. Для этого они использовали считалочку. Показывая пальцем по очереди на каждого стоящего в кругу, считающий произносит одно слово, и тот, на кого придется последнее слово, и будет водить. Требуется по данной считалочке определить, кто же будет водить.
В первой строке вводится считалочка. Она состоит из слов, записанных латинскими буквами. Слова разделены одним пробелом. Знаков препинания нет, строка начинается и заканчивается буквой. В считалочке не менее двух слов, а длина строки не превосходит \(100\).
Во второй строке в том же формате вводится список имен школьников в том порядке, в котором они стоят по кругу. Считать начинают с первого школьника. Детей не менее двух, а длина строки не превосходит \(100\).
Выведите имя школьника, которому предстоит водить.
To be or not to be John Mary Ann Kate
Mary
Na zolotom kryltse sideli Vasya Vasya Vasya
Vasya
Два автомобиля движутся по кольцевой дороге длины \(L\) в противоположных направлениях. Они начинают движение из одной точки и едут с постоянными скоростями \(v_1\) и \(v_2\) соответственно. Требуется определить, на каком расстоянии друг от друга они окажутся в момент времени \(T\).
На вход подаются \(4\) натуральных числа \(L\), \(v_1\), \(v_2\), \(T\), разделенных пробелом. Все числа не превосходят \(100\).
Выведите расстояние между автомобилями в момент времени \(T\) – длину кратчайшей из двух дуг дороги между автомобилями.
10 1 2 1
3
10 2 3 2
0
Вы когда-нибудь задумывались над тем, как отличить хорошие стихи от посредственных?
Нет? А вот редактор литературного журнала занимается этим каждый день, получая тонны корреспонденции от молодых авторов, желающих стать известными поэтами. Благо, в последнее время большая часть стихов присылается по электронной почте, поэтому у редактора возникла мысль автоматизировать процесс. Он твердо уверен, что стихи тем лучше, чем точнее в них рифма. Он считает две строки зарифмованными, если у них совпадает несколько последних букв. И чем больше букв совпадает, тем лучше зарифмованы строки. Например, у строк “палка” и “веревка” совпадают только пары последних букв “ка”, а у строк “олимпиада” и “рая и ада” совпадают четыре буквы (пробелы мы пропускаем). Поэтому вторая рифма лучше. Редактор считает, что в четверостишии (четыре строки) первая строка должна рифмоваться с третьей, а вторая – с четвертой. Для каждой из этих двух пар строк он считает количество совпадающих последних символов и из этих двух чисел выбирает наибольшее. Полученное число он называет коэффициентом качества стихотворения – чем он выше, тем больше шансов у стихотворения быть опубликованным. Помогите редактору – напишите программу, которая определяет качество стихотворения. И кто знает, может быть, благодаря вашим усилиям, мир познакомится с гениальными стихами (см. первый пример).
На вход подается \(4\) непустые строки, каждая из которых состоит из не более чем \(100\) строчных латинских букв (стихотворение уже подверглось предварительной обработке: из него удалили все пробелы и знаки препинания, а заглавные буквы сделали строчными).
Выведите одно число – коэффициент качества стихотворения.
yapomnyuchudnoemgnovenje peredomnojyavilasty kakmimoletnoevidenje kakgenijchistoykrasoty
4
eto vovse ne stihi
0
etootlichnyestihi etootlichnyestihi etootlichnyestihi etootlichnyestihi
17
На соревнованиях по прыжкам на лыжах с трамплина техника прыжка оценивается пятью судьями. Каждый судья ставит оценку от \(1\) до \(20\), после чего одна наименьшая и одна наибольшая оценки отбрасываются. Вам нужно написать программу, которая будет демонстрировать результаты прыжка для телетрансляции.
Она должна выводить пять оценок, которые поставили судьи, не меняя их порядка, а затем их сумму, и при этом брать в скобки те оценки, которые не учитываются при расчете суммы
На вход подается \(5\) натуральных чисел от \(1\) до \(20\), разделенных пробелом.
Выведите те же числа в том же порядке, взяв в скобки минимальное (а если их несколько – самое левое из них) и максимальное (а если их несколько – самое правое из них) число, а также сумму всех чисел, не взятых в скобки. Все числа (включая сумму) должны быть напечатаны в одной строке и разделены одним пробелом (внутри скобок пробелов быть не должно). Перед суммой должен стоять знак равенства, отделенный слева и справа одним пробелом. Порядок оценок должен быть такой же, как и во входных данных.
1 2 3 4 5
(1) 2 3 4 (5) = 9
10 11 10 11 10
(10) 11 10 (11) 10 = 31
Магическим квадратом называют таблицу, в которой записаны числа \(1, 2, 3, …\) по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной \((3\times 3, 5\times 5, …)\).
Поставим число \(1\) в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа \(2, 3, 4, …\). Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов \(3\times 3\) и \(5\times 5\) показаны на рисунках.
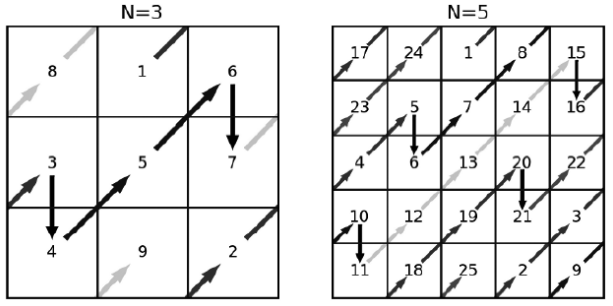
На вход подается одно натуральное нечетное число \(N\), не превосходящее \(30\) – размер квадрата.
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
3
8 1 6 3 5 7 4 9 2
5
17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9