У Славы очень много друзей, и ему очень нравится с ними встречаться. Но, к сожалению, все друзья Славы живут в разных городах (каждый в своем), до которых Слава из своего Большого Города может добраться только на электричках. Каждый раз, когда Слава решает навестить кого-нибудь из своих друзей, перед ним встает нелегкий выбор — к кому же именно поехать на этот раз. Всех своих друзей Слава очень любит и не хочет никого обидеть. Поэтому он поступает следующим образом: в некоторый момент времени Слава выходит из дома и едет на вокзал. После приезда на вокзал Слава садится в ближайшую электричку, которая едет к одному из его друзей. По известному времени приезда Славы на вокзал помогите ему узнать, к какому именно другу он сегодня поедет.
В первой строке входных данных содержатся числа M (1 ≤ M ≤ 105) — количество электричек, которые отправляются с вокзала, и время T, в которое Слава приезжает на вокзал (0 ≤ T ≤ 109). Далее следует M строк, в каждой из которых содержится два числа ti (0 ≤ ti ≤ 109, все ti различны) и fi (1 ≤ fi ≤ 109), где ti — время отправления i-й электрички(все ti различны), а fi соответствует номеру друга, к которому идет i-я электричка. Гарантируется, что есть хотя бы одна электричка, которая отправляется позже, чем момент времени T.
Выведите одно число — номер друга, к которому сегодня поедет Слава.
Считается, что Слава успевает на i-ю электричку только в том случае, если он приезжает раньше момента её отправления, т. е. T < ti.
5 74 28 3 85 2 6 1 5 3 72 1
2
Ваня не очень-то любит людей, но, к сожалению, ему иногда все-таки приходится ездить на метро. В таких случаях ему помогают две вещи: наушники с любимыми «Scoprions» и правильно выбранное место. Поскольку Ваня хочет быть как можно дальше от всех людей, правильным местом считается такое место, расстояние от которого до ближайшего из соседей будет максимально возможным в вагоне. В вагоне N мест и они все расположены вдоль одной стены, причем вход в вагон находится у места с номером 1. Места идут подряд, без пропусков. Ваня понимает, что иногда правильных мест может быть несколько, и хочет сесть на ближайшее ко входу правильное место (то есть правильное место с минимальным номером).
Угадайте, какое место в вагоне займет Ваня.
В первой строке записано число N (1 ≤ N ≤ 105). В следующей строке через пробел записаны N чисел — 0 или 1. Число 0 обозначает свободное место, 1 — занятое; места нумеруются слева направо. Гарантируется, что хотя бы одно место свободно.
Выведите номер места, на которое Ваня сядет.
8 1 0 1 0 0 1 0 1
2
7 0 1 0 0 0 1 0
4
4 0 0 0 1
1
На прошлый день рождения Олегу подарили муравьиную ферму и трех больших муравьев для нее. Ферма представляет собой поле размером a × b клеток. Клетка с координатой (1, 1) находится в левом верхнем углу. Вскоре он заметил, что передвигаясь по своему вольеру, муравьи оставляют на белом песке следы разных цветов. На протяжении нескольких месяцев Олег наблюдал за своей фермой и, наконец, смог строго описать происходящее в вольере.
Клетки бывают четырех цветов:
Муравей умеет оставлять на клетке свой след, стирать с нее все следы, поворачиваться и делать шаг вперед. То, как он изменит цвет клетки и куда он повернется, зависит только от цвета клетки, на которой он сейчас стоит. Опишем один ход муравья.
Если муравей стоит на белой клетке, то он:
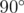вправо и делает шаг впередЕсли же муравей стоит не на белой клетке, то он:
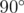влево и делает шаг вперед Если на пути муравья встречается граница фермы, шаг вперед он не делает.
Каждую минуту все три муравья по очереди делают один ход, причем сначала ходит первый, потом второй, потом третий.
Утром, уходя в школу, Олег чистит вольер так, что в начальный момент времени песок на всей ферме белый (то есть на нем нет никаких следов). Однако перемещения муравьев такие интересные, что мальчик не может нормально учиться, а вместо этого думает о своих любимцах. Сидя на занятиях, он старается понять, какой узор он увидит, когда вернется домой. Перед тем, как уйти на учебу, он записывает координаты всех своих питомцев. Олегу известно, что дома он будет ровно через T минут. Для того, чтобы Олег не отвлекался во время занятий на размышления о муравьях, напишите программу, которая сама воспроизведет рисунок, который получится на песке вольера через T минут.
В первой строке вводятся 3 числа a, b, T (1 ≤ a ≤ 100, 1 ≤ b ≤ 100, 1 ≤ T ≤ 103) — высота вольера, ширина вольера и время, которое Олега не будет дома, соответственно. Следующие три строки содержат описание положения муравьев. В каждой строке записано по 2 числа i, j (1 ≤ i ≤ a, 1 ≤ j ≤ b) — координаты муравьев (сначала записан номер строки, а затем номер столбца), причем в первой из строчек записаны координаты первого муравья, во второй — второго, а в третьей — третьего. Гарантируется, что в одной и той же клетке изначально не находилось двух муравьев. Изначально все муравьи смотрят вверх.
Выведите состояние поля на момент времени T: a строк по b чисел в каждой через пробел. Каждое число обозначает цвет следа, оставленного в данной клетке вольера.
3 3 2 1 2 2 2 3 2
0 1 1 0 2 2 0 3 3