#529

Темы: [Двумерные массивы]

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача E ]

Сережа играет в "Морской бой". Поле для игры представляет собой квадрат 10 x 10 клеток. На поле отмечены клетки, в которые Сережа уже стрелял. Однако, пока он не попал ни в один корабль противника. Требуется определить максимальную длину корабля, который может поместиться в небитых клетках этого поля. Корабль представляет из себя прямоугольник ширины 1 и располагается горизонтально или вертикально. (Гарантируется, что на поле есть хотя бы одна небитая клетка.)

Входные данные

Вводятся 10 строк по 10 чисел в каждой, числа разделены пробелами. Число 1 означает, что в соответствующую клетку стреляли, число 0 – что в клетку не стреляли.

Выходные данные

Требуется вывести одно число от 1 до 10 – максимальную возможную длину корабля.

Примеры

Входные данные

0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 0 0 1 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 1 0 0 1 0 0 0
0 0 1 0 0 0 0 1 0 0
0 1 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0

Выходные данные

#530

Сеня наблюдает за кузнечиками

Темы: [Условный оператор (if)] [Циклы]

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача F ]

На прямой тропинке на расстоянии 1 метр друг от друга сидят два кузнечика. Время от времени один из кузнечиков прыгает на несколько сантиметров влево или вправо. Требуется узнать, каково было минимальное расстояние, на которое сближались кузнечики в процессе прыжков. (Расстояние считается только в те моменты, когда оба кузнечика сидят на земле).

Входные данные

В первой строке вводится одно число \(N\) (1 ≤ \(N\) ≤ 100) – общее количество прыжков, а затем \(N\) чисел, описывающих прыжки. Модуль числа равен длине прыжка в сантиметрах; число отрицательное, если кузнечик начинал этот прыжок по направлению к другому кузнечику, и положительное – если от другого кузнечика. Числа по модулю не превосходят 100 и все отличны от 0. (Кузнечики могут перепрыгивать друг через друга. Гарантируется, что кузнечики не приземляются друг на друга.)

Выходные данные

Требуется вывести одно число – минимальное расстояние в сантиметрах, на которое сближались кузнечики.

Примеры

Входные данные

Выходные данные

#534

Ваня наблюдает за лягушкой

Темы: [Целые числа]

Источники: [ Командные олимпиады, Московская командная олимпиада, 8 класс, 2006, Задача J ]

Ваня наблюдает за лягушкой. Изначально она сидит в точке 0 числовой прямой. Каждую секунду она прыгает на 1 вправо, пока не достигнет точки K. Затем она начинает каждую секунду прыгать на 1 влево, пока не вернется в точку 0, затем – опять вправо и т. д. Требуется определить, где окажется лягушка через T секунд.

Входные данные

Вводятся два числа \(K\) и \(T\), разделенные пробелом. Оба числа натуральные и не превосходят 1 000 000 000.

Выходные данные

Вывести одно число – координату лягушки в момент времени \(T\).

Примеры

Входные данные

10 6

Выходные данные

#854

Складирование ноутбуков

Темы: [Простые задачи на перебор]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2008, Лига А, Задача A ]

На склад, который имеет форму прямоугольного параллелепипеда, привезли ноутбуки, упакованные в коробки. Каждая коробка также имеет форму прямоугольного параллелепипеда.

По правилам хранения коробки с ноутбуками должны быть размещены на складе с выполнением следующих двух условий:

Стороны коробок должны быть параллельны сторонам склада

Коробку при помещении на склад разрешается расположить где угодно (с выполнением предыдущего условия), в том числе на другой коробке, но все коробки должны быть ориентированы одинаково (т.е. нельзя одну коробку расположить «стоя», а другую – «лежа»)

Напишите программу, которая по размерам склада и размерам коробки с ноутбуком определит максимальное количество ноутбуков, которое может быть размещено на складе.

Входные данные

Вводится шесть натуральных чисел. Первые три задают длину, высоту и ширину склада. Следующие три задают соответственно длину, высоту и ширину коробки с ноутбуком. Каждое из чисел не превышает 1000.

Выходные данные

Выведите одно число — максимальное количество ноутбуков, которое может быть размещено на складе.

Примеры

Входные данные	Выходные данные
100 200 300 1 2 3	1000000
100 200 300 3 2 1	1000000
100 100 1 2 2 2	0
7 7 7 3 3 3	8

#855

Сортировка вагонов

Темы: [Стек] [Задачи на моделирование]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2008, Лига А, Задача B ]

Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

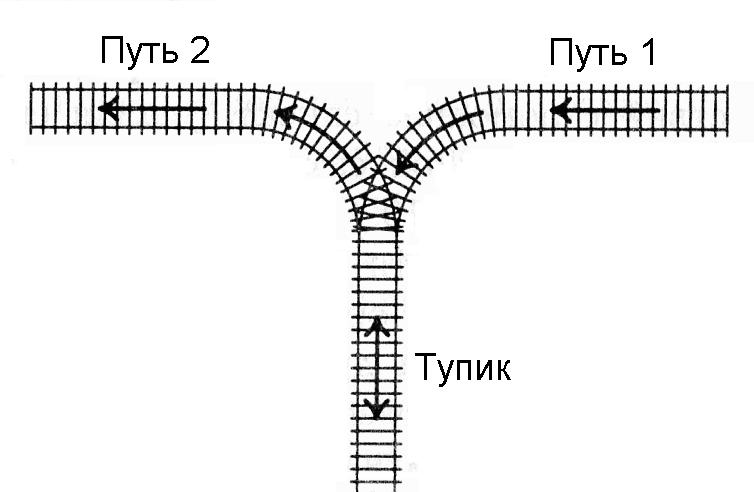
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0