На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.

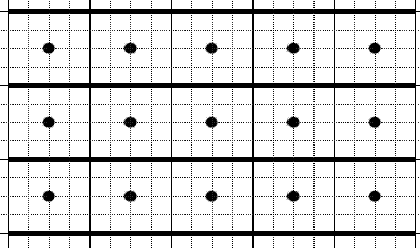
На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.

Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).

В Тридевятом Царстве было N городов, некоторые из которых были соединены дорогами. К сожалению, в последнее время добраться из одного города в другой стало очень сложно из-за возникших автомобильных пробок. В целях борьбы с пробками было решено все дороги сделать односторонними, т.е. разрешить проезд по каждой дороге только в одном направлении. При этом требуется, чтобы по-прежнему можно было из любого города попасть в любой другой.

Вася и Петя играют в следующую игру. Они берут колоду из 36 карточек. На каждой карточке написано число от 1 до 9 и каждая карточка покрашена в один из 4 цветов так, что есть ровно по 9 карточек каждого цвета и они пронумерованы числами от 1 до 9. Карты перемешиваются, и игрокам раздается по 18 карт.

Дальше игроки по очереди делают ходы. За один ход игрок может выложить на стол одну карточку по следующим правилам. Карточку с цифрой 5 можно выкладывать на стол в любой момент. Карточку с другой цифрой можно выкладывать только если на стол уже выложена карточка того же цвета, на которой написано число на 1 большее или на 1 меньшее, чем на данной карточке (не важно, была ли эта карточка выложена вами или вашим противником, и была ли она выложена на предыдущем ходе или раньше). Если игрок может выложить хоть какую-то карточку, он обязан делать ход. Если ни одну карточку игрок выложить не может, он пропускает ход.

Выигрывает тот, кто первым выложит все свои карточки на стол.

Напишите программу, которая по информации о том, кому какие карточки достались, определяет, кто выиграет при оптимальной игре обоих игроков.

Маршрут автобуса проходит через N остановок (включая конечные). Отдел по исследованию пассажиропотоков записал данные о том, сколько человек выходило и сколько садилось в автобус на каждой остановке. Напишите программу, которая по этим данным определит, какое максимальное количество человек одновременно в этот рейс ехало в автобусе.