Скоро у Лизы день рождения! Родители долго думали, чем порадовать свою любимую дочку, и решили, что лучше всего подарить ей путешествие в Нью-Йорк. Ведь это — такой оригинальный подарок! Так как Лиза — уже самостоятельная девочка, она вполне может сама выбрать, где ей поселиться в Нью-Йорке. Однако родители очень беспокоятся за нее, поэтому они разрешили ей выбирать только из H безопасных пятизвездочных отелей.
Лиза — общительная девочка, и у неё очень много друзей. Узнав, что она будет отмечать день рождения в Нью-Йорке, друзья немедленно отправились туда и поселились в C хостелах.
Лиза по случаю дня рождения устраивает маленькую вечеринку. К сожалению, никто из её друзей не хочет пропустить очередную серию нового реалити-шоу «Home-2», но как только серия закончится, все они одновременно выйдут из своих хостелов и поедут поздравлять Лизу. Она — девочка нетерпеливая, поэтому хочет выбрать отель так, чтобы последний друг приехал к ней как можно раньше, т.е. находился как можно ближе. Так как она тоже не хочет отвлекаться от просмотра высокоинтеллектуального шоу, она попросила вас помочь ей с выбором отеля. Конечно, за это она тоже пригласит вас на вечеринку!
Как известно, Нью-Йорк представляет собой идеальную прямоугольную сетку улиц: с севера на юг тянутся N авеню, а с запада на восток — M улиц. Наличием Бродвея мы в этой задаче пренебрежем. Можно считать, что каждый объект находится в узле этой сетки (и, таким образом, однозначно задается номером авеню и номером улицы, возле пересечения которых он расположен), а два соседних узла сетки находятся на расстоянии одного километра.
В первой строке входных данных содержится два числа N и M — размеры города ( 1 ≤ N , M ≤ 10 9 ). В следующей строке содержится единственное число C — количество хостелов ( 1 ≤ C ≤ 10 5 ). Далее в C строках содержатся описания хостелов, каждый из них задается двумя координатами x и y ( 1 ≤ x ≤ N , 1 ≤ y ≤ M ). В следующей строке содержится одно число H — количество отелей ( 1 ≤ H ≤ 10 5 ). В следующих строках содержатся описания отелей, в том же формате, что и хостелы.
Отель и хостел могут располагаться возле одного и того же перекрестка.
В первой строке выходных данных выведите одно число — искомое оптимальное расстояние. В следующей строке выведите номер любого из отелей, гарантирующих данное расстояние.
10 10 2 1 1 3 3 2 1 10 4 4
6 2
Как-то раз удав, слонёнок, мартышка и попугай играли в замечательную игру <<змейка>>.
Суть этой известной игры в следующем. Удав перемещается по прямоугольному полю, не переползая через самого себя, и ест яблоки, которые ему сверху скидывает попугай.
Как известно, мерять длину удава можно в слонёнках, мартышках или попугаях. Но в попугаях удав выходит гора-а-а-здо длиннее, поэтому мы остановимся на них в качестве единицы измерения. Поле представляет собой \(N\) строк по \(M\) ячеек размером \(1\) попугай \(\times\) \(1\) попугай. Изначально длина удава составляет всего три попугая (каким образом удав становится таким коротким в начале игры - долгая и запутанная история, поэтому мы не будем на ней останавливаться в рамках этой задачи...), он занимает три крайних левых ячейки в верхней строке поля и смотрит направо. Каждый раз, съедая яблоко, удав удлиняется на одного попугая и занимает тем самым ещё одну клетку поля.
Более формально - удав длины \(L\) попугаев представляет собой последовательность из \(L\) различных клеток поля \(A_1, A_2 \dots A_L\), таких что любые две соседних в этой последовательности клетки \(A_i\) и \(A_{i+1}\) являются соседними на поле, т.е. имеют общую сторону. Головой удава считается клетка \(A_L\). За один ход удав может продвинуться на одну клетку - он выбирает новую клетку \(H\) для своей головы (естественно, смежную с текущей клеткой головы \(A_L\) и не выходящую за границы поля), а его хвост подтягивается следом на одну клетку. То есть, после хода удав будет представлять собой последовательность из клеток \(A_2, A_3, \dots, A_L, H\). Обратите внимание, по определению выше удав после выполнения хода не должен дважды содержать одну и ту же клетку, но новое положение головы \(H\) вполне может совпадать со старым положением хвоста \(A_1\) (наш удав перемещается подобно гусенице, сначала сжимаясь и подтягивая хвост, а потом разжимаясь и продвигая голову, поэтому это корректный ход).
Заметим, что из этого определения сразу следует, что в каждый момент времени у удава есть возможность пойти в не более чем трёх направлениях - продолжить движение в направлении, куда смотрит его голова, свернуть налево или свернуть направо.
В любой момент времени на поле находится ровно одно яблоко. Каждый раз, когда удав съедает яблоко, его длина увеличивается на одного попугая. Это происходит следующим образом: если удав делает ход, после которого его голова занимает клетку, в которой расположено яблоко, оно считается съеденным. В таком случае яблоко сразу продвигается по телу удава вплоть до бывшего положения хвоста (т.е. до клетки \(A_1\)), и на этом месте возникает новая клетка удава. Таким образом, удав приобретает длину в \((L + 1)\) попугай и занимает к началу следующего хода клетки (\(A_1, A_2, \dots A_K, H\)). В этот же момент попугай скидывает следующее яблоко на какую-то из незанятых клеток поля.
Удав проигрывает, если он делает некорректный ход. Помогите удаву cъесть все яблоки!
Это - интерактивная задача.
В первой строке стандартного потока ввода идут два целых числа \(N\) и \(M\) (\(3 \le N, M \le 25\)) - количество строк и столбцов поля соответственно.
Далее ваше общение с тестирующей программой будет устроено следующим образом. На каждое яблоко, скидываемое попугаем, вашей программе будут подаваться на стандартный на стандартный поток ввода два целых числа \(R\) и \(C\) (\(1 \le R \le N, 1 \le C \le M\)) - соответственно номер строки и столбца клетки, содержащей яблоко. Строки нумеруются с 1 по \(N\) сверху вниз, столбцы нумеруются с 1 по \(M\) слева направо.
После этого вы должны вывести последовательность команд для удава в виде строки, состоящей из латинских букв 'R', 'U', 'L' и 'D', которые обозначают что удав должен сделать ход, передвинув свою голову соответственно на клетку правее, выше, левее или ниже. По итогам этой последовательности команд удав должен съесть яблоко, не допуская некорректных ходов. Обратите внимание, яблоко должно быть съедено именно последним ходом этой последовательности! После вывода каждой строки сбрасывайте буфер вывода - для этого используйте flush(output) на языке Паскаль или Delphi, fflush(stdout) или cout.flush() в C/C++, sys.stdout.flush() на языке Python, System.out.flush() на языке Java.
В момент окончания игры (как успешного, так и неуспешного - например, если удав делает некорректный ход) вашей программе на ввод подаётся строка, состоящая из двух нулей. Обратите внимание, считав эти два нуля, ваша программа обязательно должна сразу завершиться! В противном случае в качестве результата проверки вы можете получить вердикт, отличный от настоящего!
Пояснение к первому тесту. Положение удава по ходу игры показано ниже.
Пояснение ко второму тесту. Обратите внимание, что после шестого хода происходит ситуация, проиллюстрированная в условии: в качестве нового положения головы выбирается клетка \((2, 3)\), являющаяся на тот момент клеткой хвоста.
4 6 0 3 3 3 4 6 1 3
turn = 0, len = 3: new apple appeared at (3 3) RRRDDDLUULDDLU turn = 14, len = 4: ate apple at (3 3) turn = 14, len = 4: new apple appeared at (4 6) ULDDLUUURRRRRDDD turn = 30, len = 5: ate apple at (4 6) turn = 30, len = 5: new apple appeared at (1 3) LU
3 5 0 4 2 3 3 4 3 5 2 2
turn = 0, len = 3: new apple appeared at (2 3) RRDDLUL turn = 7, len = 4: ate apple at (2 3) turn = 7, len = 4: new apple appeared at (2 2) DLU turn = 10, len = 5: ate apple at (2 2) turn = 10, len = 5: last apple eaten turn = 10, len = 5: finished!
Тимофей — настоящий сладкоежка. Сегодня он купил большой и вкусный круглый торт с клубникой, чтобы полакомиться самому и угостить друзей.

Однако Тимофей угощает друзей очень изощренным способом. А именно, он отрезает кусочки с краев торта прямолинейными разрезами ножа. При этом, чтобы разрезы получились красивыми, нож нужно вести непрерывно, разрезы не должны друг друга пересекать, а закончить процесс отрезания нужно в начальной его точке. Более того, так как Тимофей — большой любитель клубники, то он хочет, чтобы все ягоды оказались внутри центрального куска тортика, который, конечно же, достанется ему самому.
Однако оказалось, что разрезать торт таким образом весьма непросто. Помогите Тимофею! Быть может, в награду он и вас угостит кусочком этого замечательного тортика.
Будем считать, что торт является кругом на плоскости, а ягоды представляют собой точки. Необходимо построить любой выпуклый многоугольник, вершины которого лежат на окружности, ограничивающей круг, а все заданные точки находятся внутри него или на его границе.
В первой строке входных данных содержатся четыре числа N , R , X , Y : количество ягод, радиус торта и координаты центра торта ( 1 ≤ N ≤ 100 , 1 ≤ R ≤ 1 000 , 0 ≤ | X |, | Y | ≤ 1 000 ). В следующих N строках содержатся описания ягод. Каждая ягода задается двумя числами x i , y i — своими координатами ( 0 ≤ | x i |, | y i | ≤ 1 000 ).
В первой строке выходных данных выведите единственное число M — количество вершин в построенном вами многоугольнике ( 3 ≤ M ≤ 222 ). В следующих M строках выведите координаты вершин многоугольника, в порядке обхода против часовой стрелки.
Ваш ответ будет считаться верным, если все выведенные вами точки различны, действительно лежат на окружности, если они образуют выпуклый многоугольник, и если все ягоды лежат внутри или на границе многоугольника.
Проверяющая программа производит все проверки с точностью 10 - 6 , в частности, независимо от того, сколько знаков вы выведите после десятичной точки, две вершины многоугольника будут считаться совпадающими, если они отличаются и по x -координате, и по y координате не более, чем на 10 - 6 .
4 6 2 3 2 4 3 4 1 2 -4 3
6 -4.000000 3.000000 -2.242641 -1.242641 2.000000 -3.000000 8.000000 3.000000 6.242641 7.242641 2.000000 9.000000
Будущие программисты Андрей и Борис вчера впервые поехали кататься с родителями по новой кольцевой дороге. Каждый из них выехал на дорогу в определённом месте, сделал полный круг и вернулся домой. От скуки они оба считали фонарные столбы, расположенные посередине дороги между встречными полосами движения, так что все N фонарных столбов у каждого из мальчиков получили номера от 1 до N . Но само значение N они не запомнили. При этом два столба обоим мальчикам запомнились особенно: на одном из них висел яркий плакат ко Дню города, а на другом — флаг Москвы. Каждый из мальчиков записал себе в тетрадку номер каждого из этих двух столбов.
Сегодня обе семьи, Андрея и Бориса, пошли на выставку кошек, и там мальчики, обсудив свои поездки, задались вопросом: сколько же всего фонарных столбов на новой кольцевой дороге? Единственное, что они смогли выяснить, в одном ли направлении ехали они по дороге.
Так сложилось, что Андрей — ваш младший брат, поэтому именно вам предстоит ответить на вопрос мальчиков. У вас есть серьёзное подозрение, что может не получиться однозначно найти ответ, а мальчики боятся больших чисел, поэтому вы решили сказать им лишь минимальное из возможных значений числа N .
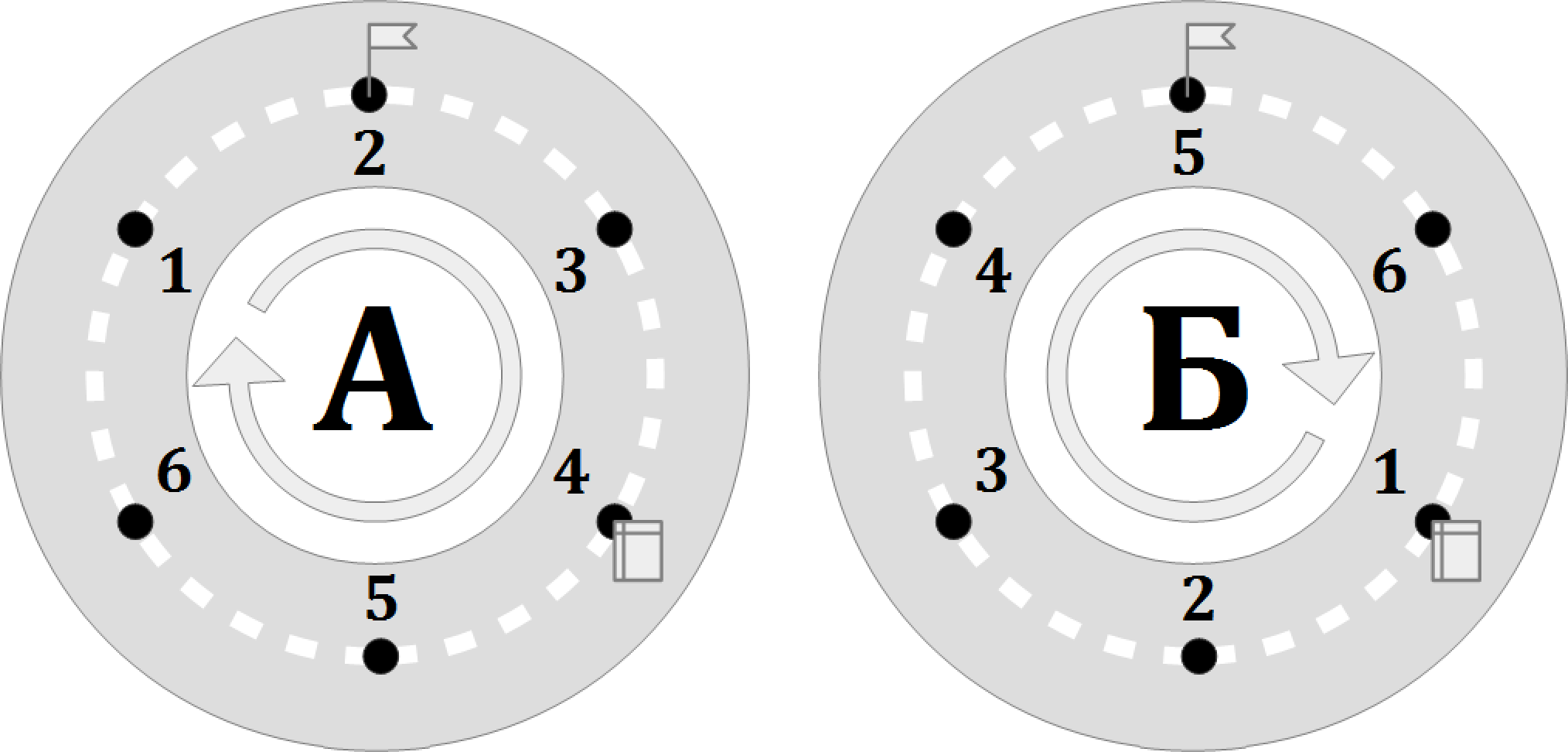
В этом примере N = 6 , A p = 4 , A f = 2 , B p = 1 , B f = 5 .
Первая строка ввода содержит единственное целое число D , которое равно 1 , если мальчики ехали в одном направлении, и - 1 , если в разных. Следующие 4 строки содержат 4 натуральных числа A p , B p , A f , B f , по одному числу в строке, каждое из которых не превосходит 10 6 : A p — номер столба с плакатом в нумерации Андрея, B p — номер этого столба в нумерации Бориса, A f — номер столба с флагом в нумерации Андрея, B f — номер этого столба в нумерации Бориса.
Плакат и флаг могли оказаться на одном столбе — в этом случае каждый из мальчиков должен был бы получить два одинаковых числа, т. е. A p = A f и B p = B f .
Выведите единственное натуральное число N — минимально возможное количество столбов. Если мальчики где-то ошиблись, и таких чисел, как у них, не могло получиться ни при каком зна-че-нии N , выведите число - 1 .
1 4 1 2 5
6
-1 4 9 4 7
-1
Команда туристического клуба «В гору пойдёт!» только что вернулась из очередного похода. Прямо сейчас участники экспедиции с жаром спорят о том, какой же горный хребет они покорили.
Достоверно известно, что на маршруте было N стоянок, причём все — на разной целочисленной высоте от 1 до N над уровнем моря. Альпинисты заблаговременно прибыли на место первой стоянки, а потом шли по маршруту в течении N - 1 дня: в первый день они шли от 1 -й стоянки до 2 -й, во второй — от 2 -й до 3 -й и так далее, пока в последний день не совершили переход от стоянки под номером N - 1 до стоянки под номером N , завершив этим свой маршрут.
Участники экспедиции пытаются понять, на какой высоте находилась каждая стоянка. В их распоряжении имеется запись в журнале, содержащая информацию о том, сколько дней они шли в гору, а сколько — спускались.
Помогите альпинистам! Подскажите им хоть какой-нибудь вариант маршрута, не противоречащий записи в журнале.
Входные данные содержат две строки. В первой строке записано целое неотрицательное число A — это количество дней, в которые альпинисты поднимались в гору. Вторая строка содержит целое неотрицательное число B — количество дней, в которые альпинисты спускались ( A + B + 1 = N , 1 ≤ N ≤ 100 000 ).
Выведите N различных целых чисел от 1 до N , разделённых пробелами, — маршрут, по которому могли пройти альпинисты. Маршрут описывается высотами стоянок в том порядке, в котором их могли посетить участники экспедиции.
0 1
2 1
3 0
1 2 3 4