Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 95 задач <---
Источники --> Командные олимпиады --> Московская командная олимпиада --> 9-11 классы
    2003(8 задач)
    2004(9 задач)
    2005(10 задач)
    2006(10 задач)
    2007(19 задач)
    2008(19 задач)
    2009(18 задач)
    2010(18 задач)
    2011(18 задач)
    2012(19 задач)
    2013(19 задач)
    2014(20 задач)
    2015(21 задач)
    2016(20 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#43
Лапта
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

При игре в лапту одна команда ловит мяч и пытается осалить им бегущего. Игрок другой команды должен, перед тем как бежать, ударить мяч в поле. Известно, на какое максимальное расстояние он может ударить, а также скорости и начальные координаты игроков другой команды. Требуется выбрать направление и силу удара так, чтобы минимальное время, которое потребуется другой команде, чтобы поднять мяч с земли, было наибольшим. (Пока мяч летит, игроки стоят на местах.)

Входные данные

В первой строке входных данных содержатся два числа: D — максимальное расстояние удара и N — количество соперников на поле (D и N натуральные числа, D ≤ 1000, N ≤ 200). В следующих N строках задается по три числа – начальные координаты xi и yi и максимальная скорость vi соответствующего игрока (скорости и координаты — целые числа, –1000 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000, 0 < vi ≤ 1000), никакие два игрока не находятся изначально в одной точке. Игрок, бьющий мяч, находится в точке с координатами (0,0). Мяч выбивается в точку с неотрицательной ординатой (y ≥  0).

Выходные данные

Выведите сначала время, которое потребуется игрокам, чтобы добежать до мяча, а затем координаты точки, в которую нужно выбить мяч. Если таких точек несколько, выведите координаты любой из них. Время и координаты нужно вывести с точностью 10–3.

Оценка задачи

1 балл получат программы, которые верно работают, когда в поле не более двух соперников.

Примеры
Входные данные
10 2
1 1 1
-1 1 1
Выходные данные
9.05539
0.00000 10.00000
#44
Машинки
  
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
64 megabytes

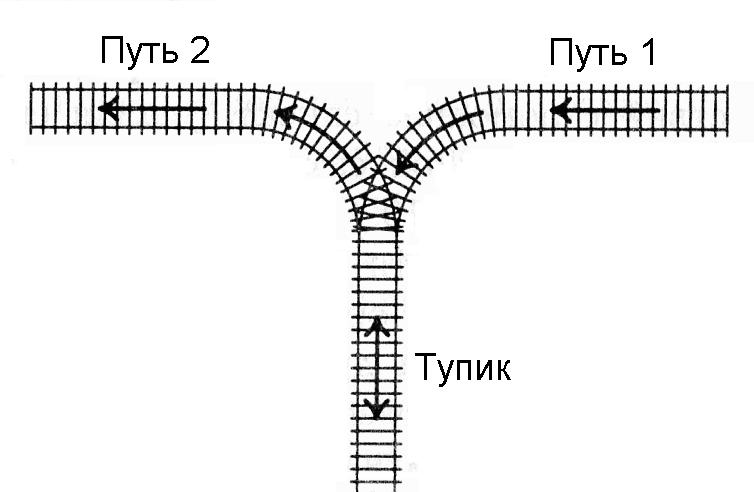
По двум однополосным дорогам едут машины. На перекрестке эти дороги сливаются в одну однополосную (машины едут как раз в ее сторону). На этом самом перекрестке стоит постовой милиционер, который регулирует движение, а именно, выбирает, с какой из двух дорог в данный момент машины будут заезжать.

В каждый момент времени либо одна из дорог является "активной", т.е. перекресток проезжают машины с этой дороги, либо регулировщик производит переключение потока на другую дорогу (в этот момент никакие машины через перекресток не едут). На то, чтобы "переключить" поток, тратится время Т.

В некоторый момент образовалась пробка. На 1-й дороге скопилось N машин, а на 2-й — M. Для каждой машины известно время, которое ей потребуется для проезда развилки, если она первая в очереди и ее дорога "активна".

Требуется разработать план действий для постового по переключению потоков, при котором среднее время ожидания машины минимально (временем ожидания машины называется время с момента образования пробки до того момента, когда данная машина заканчивает проезжать перекресток; для вычисления среднего времени суммируются времена ожидания всех машин и полученная сумма делится на общее количество машин). В начальный момент активна первая дорога.

Входные данные

Сначала вводятся числа T, N и M, затем N чисел — времена проезда перекрестка машинами с первой дороги (в порядке удаления от перекрестка), а затем M чисел — времена проезда перекрестка машинами со второй дороги.

<>Все числа  целые неотрицательные, все времена не превосходят 100, T ≤ 100, N, M ≤ 1000, N+M > 0.

Выходные данные

В первой строке  выведите одно число — минимальное среднее время ожидания c точностью 10–3. Далее выводите информацию о машинах в порядке их проезда перекрестка и о переключении потока  следующим образом.

  • Для каждой машины выведите информацию в формате:

Car k from road i

где k — номер машины на своей дороге (ближайшая к перекрестку в момент образования пробки машина имеет номер 1, следующая на той же дороге — 2 и т.д.), i — номер дороги: 1 или 2.

  • Для каждого переключения потока выведите информацию:

Switch road from 1 to 2

для переключения потока с первой дороги на вторую или

Switch road from 2 to 1

для переключения потока со второй дороги на первую.

Информация обо всех событиях (переключениях и проездах через перекресток) должна выводиться именно в том порядке, в котором они происходят.

Если решений несколько, выведите любое из них.

Оценка задачи

1 балл будет набирать решение, верно работающее при N, M ≤ 10.

Примеры
Входные данные
1 2 2
5 6 
1 7
Выходные данные
11.500
Switch road from 1 to 2
Car 1 from road 2
Switch road from 2 to 1
Car 1 from road 1
Car 2 from road 1
Switch road from 1 to 2
Car 2 from road 2
#45
Контейнеры
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На складе хранятся контейнеры с товарами N различных видов. Все контейнеры составлены в N стопок. В каждой стопке могут находиться контейнеры с товарами любых видов (стопка может быть изначально пустой).Автопогрузчик может взять верхний контейнер из любой стопки и поставить его сверху в любую стопку. Необходимо расставить все контейнеры с товаром первого вида в первую стопку, второго вида — во вторую стопку и т.д.

Программа должна вывести последовательность действий автопогрузчика или сообщение о том, что задача решения не имеет.

Входные данные

В первой строке задается одно натуральное число N, не превосходящее 500. В следующих N строках описаны стопки контейнеров: сначала записано число ki — количество контейнеров в стопке, а затем ki чисел — виды товара в контейнерах в данной стопке, снизу вверх. В каждой стопке вначале не более 500 контейнеров (в процессе переноса контейнеров это ограничение может быть нарушено).

Выходные данные

Выведите описание действий автопогрузчика: для каждого действия укажите два числа — из какой стопки брать контейнер и в какую стопку класть. (Обратите внимание, что минимизировать количество операций автопогрузчика не требуется.) Если задача не имеет решения, выдайте одно число 0. Если контейнеры изначально правильно размещены по стопкам, выводить ничего не надо.

Оценка задачи

1 балл будут получать программы, верно работающие при следующих ограничениях: количество стопок не больше 10, в каждой стопке не более 10 контейнеров.

Комментарий к примеру:

Изначально в первой стопке лежат четыре контейнера — снизу контейнер с товаром первого вида, над ним — с товаром второго вида, над ним — третьего, и сверху — еще один контейнер с товаром второго вида.

Одна из правильных последовательностей действий (вместо ответа в примере задачи):

1 2
1 3
1 2

Примеры
Входные данные
3
4 1 2 3 2
0
0
Выходные данные
1
#854
Складирование ноутбуков
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На склад, который имеет форму прямоугольного параллелепипеда, привезли ноутбуки, упакованные в коробки. Каждая коробка также имеет форму прямоугольного параллелепипеда.

По правилам хранения коробки с ноутбуками должны быть размещены на складе с выполнением следующих двух условий:

Стороны коробок должны быть параллельны сторонам склада

Коробку при помещении на склад разрешается расположить где угодно (с выполнением предыдущего условия), в том числе на другой коробке, но все коробки должны быть ориентированы одинаково (т.е. нельзя одну коробку расположить «стоя», а другую – «лежа»)

Напишите программу, которая по размерам склада и размерам коробки с ноутбуком определит максимальное количество ноутбуков, которое может быть размещено на складе.

Входные данные

Вводится шесть натуральных чисел. Первые три задают длину, высоту и ширину склада. Следующие три задают соответственно длину, высоту и ширину коробки с ноутбуком. Каждое из чисел не превышает 1000.

Выходные данные

Выведите одно число — максимальное количество ноутбуков, которое может быть размещено на складе.

Примеры

Входные данные

Выходные данные

100 200 300

1 2 3

1000000

100 200 300

3 2 1

1000000

100 100 1

2 2 2

0

7 7 7

3 3 3

8
#855
Сортировка вагонов
  
Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

  • если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
  • если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест