В первом классе Глеб увлекался шахматами. К тому моменту он знал только лишь как ходит пешка: она может бить по диагонали влево-наверх и вправо-наверх, и ходить на клетку вверх только если та клетка не занята другой фигурой. Поэтому он придумал свой вариант шахмат.
Игра идёт на доске с N строками и M столбцами (1 ≤ N ≤ 100, 1 ≤ M ≤ 100) по следующим правилам. В нижней строке, имеющей номер 1, стоит P белых пешек, белых фигур на доске больше нет. На остальной части доски стоят разные чёрные фигуры (их названия Глеб не знает). Ходят только белые, цель — достичь хотя бы одной пешкой самой верхней строки, имеющей номер N (Глеб слышал, что в этой ситуации из пешки можно сделать ферзя, а с такой силой он безусловно сможет побить все остальные чёрные фигуры).
Как и в настоящих шахматах, если пешка Глеба бьёт чёрную фигуру, то она становится на её место, а побитая фигура убирается с доски. Считается, что Глеб выиграл, если он сумел достичь хотя бы одной пешкой самой верхней строки, в противном случае он проиграл. Помогите ему по заданной конфигурации всех фигур определить, сможет ли он выиграть.
Сначала вводятся четыре целых числа N, M, P, K (1 ≤ N ≤ 100, 1 ≤ M ≤ 100, 0 ≤ P ≤ M, 1 ≤ K ≤ (N - 1)M. Далее записано P различных чисел — номера столбцов pj (1 ≤ pj ≤ M), в которых стоят белые пешки. Далее идут K различных пар целых чисел — номера строк и столбцов чёрных фигур ri, ci (2 ≤ ri ≤ N, 1 ≤ ci ≤ M).
Если хотя бы одна пешка сможет достичь последнего ряда, выведите YES, в противном случае выведите NO.
3 3 2 3 1 3 2 2 3 1 3 3
YES
4 4 2 4 1 4 3 1 3 2 4 2 4 4
NO
Город будущего застроен небоскребами, для передвижения между которыми и парковки транспорта многие тройки небоскребов соединены треугольной подушкой из однополярных магнитов. Каждая подушка соединяет ровно 3 небоскреба и вид сверху на нее представляет собой треугольник, с вершинами в небоскребах. Это позволяет беспрепятственно передвигаться между соответствующими небоскребами. Подушки можно делать на разных уровнях, поэтому один небоскреб может быть соединен различными подушками с парами других, причем два небоскреба могут соединять несколько подушек (как с разными третьими небоскребами, так и с одинаковым). Например, возможны две подушки на разных уровнях между небоскребами 1, 2 и 3, и, кроме того, магнитная подушка между 1, 2, 5.
Система магнитных подушек организована так, что с их помощью можно добираться от одного небоскреба, до любого другого в этом городе (с одной подушки на другую можно перемещаться внутри небоскреба), но поддержание каждой из них требует больших затрат энергии.
Требуется написать программу, которая определит, какие из магнитных подушек нельзя удалять из подушечной системы города, так как удаление даже только этой подушки может привести к тому, что найдутся небоскребы из которых теперь нельзя добраться до некоторых других небоскребов, и жителям станет очень грустно.
В первой строке входного файла находятся числа N и M — количество небоскребов в городе и количество работающих магнитных подушек соответственно (3 ≤ N ≤ 100000, 1 ≤ M ≤ 100000). В каждой из следующих M строк через пробел записаны три числа — номера небоскребов, соединенных подушкой. Небоскребы пронумерованы от 1 до N. Гарантируется, что имеющиеся воздушные подушки позволяют перемещаться от одного небоскреба до любого другого.
Выведите в выходной файл сначала количество тех магнитных подушек, отключение которых невозможно без нарушения сообщения в городе, а потом их номера. Нумерация должна соответствовать тому порядку, в котором подушки перечислены во входном файле. Нумерация начинается с единицы.
3 1 1 2 3
1 1
3 2 1 2 3 3 2 1
0
5 4 1 2 3 2 4 3 1 2 4 3 5 1
1 4
В одном уездном городе Эн было решено построить собственное метро. Все силы города были мобилизованы на выкапывание станций и прокладку подземных путей дедовскими лопатами.
Вся эта история нас бы совершенно не интересовала, если бы однажды в мэрию города не пришло письмо из далёкой страны Емакира. Оказалось, что компания Alpep подозревает администрацию уездного города в нарушении их патента на jMetro и грозится возбудить против города Эн дело. Согласно патенту, jMetro — это метро, в котором:
Поскольку компания Alpep известна своими необоснованными обвинениями в нарушениях патентов, мэрия города хочет проверить правомочность заявления компании.
В первой строке заданы два числа N и M ( 1 ≤ N , M ≤ 2·10 5 ) — количество станций метро и перегонов между ними. Следующие M строк содержат описания перегонов: каждая из них содержит по два числа — номера станций, между которыми есть перегон. По каждому перегону составы могут ездить как в одну, так и в другую сторону. Между любыми двумя станциями существует не более одного перегона. Никакой перегон не соединяет станцию саму с собой.
Выведите « YES », если метро уездного города Эн нарушает патент jMetro, и « NO » в противном случае.
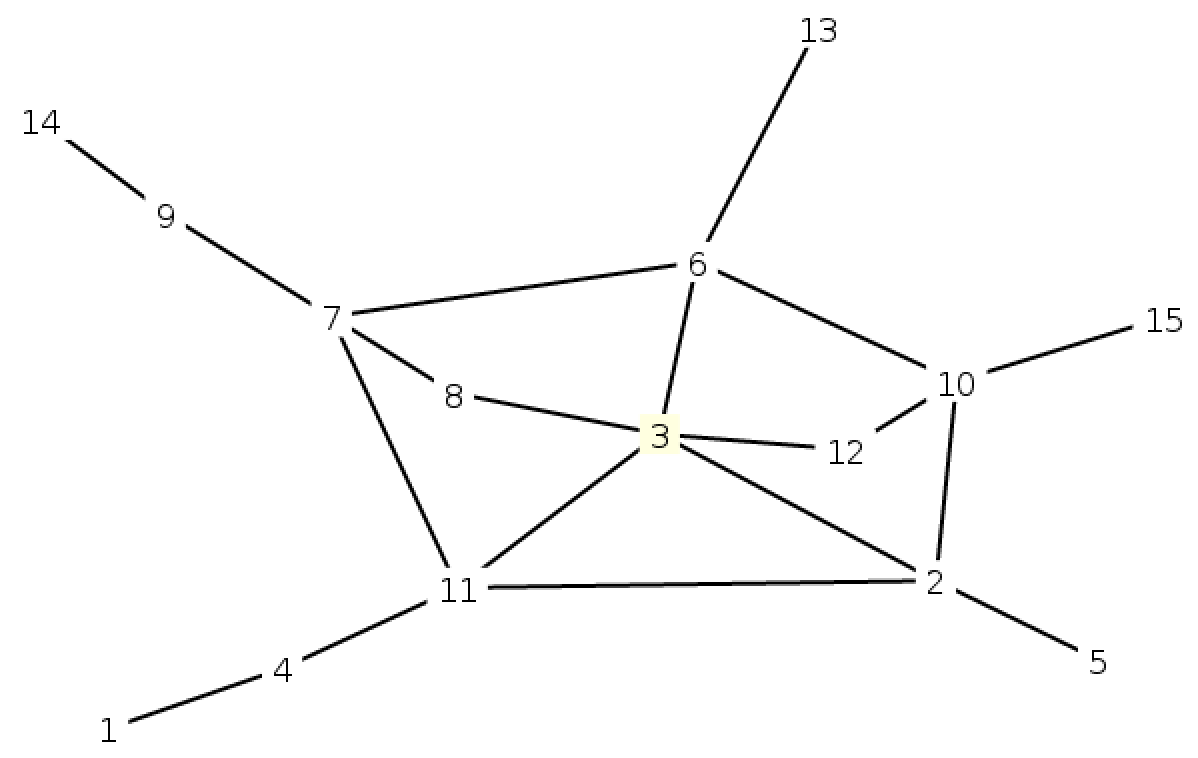
Первый пример соответствует рисунку из условия.
15 19 1 4 4 11 2 10 3 2 8 7 7 6 12 10 15 10 11 2 14 9 6 13 7 9 7 11 2 5 8 3 6 10 3 6 11 3 12 3
YES
5 4 2 1 2 3 2 5 2 4
NO