При игре в новую игру (некоторый гибрид боулинга и бильярда) используется N шариков, пронумерованных числами от 1 до N. В начале игры эти шарики должны быть выложены в линию в порядке своих номеров. В процессе игры их порядок может меняться.

Для того, чтобы упорядочить шарики перед началом следующей партии, используется следующее устройство. Это устройство состоит из головки, которая, перемещаясь над шариками, может «засасывать» и «выплевывать» шарики. Чтобы получить большее представление об этом устройстве, представьте себе пылесос, который может засасывать шарики, перемешаться в нужное место, и там, включаясь на продув в обратном направлении, шарики «выплевывать».

При засасывании шарика все шарики, которые находились правее засасываемого, сдвигаются влево. «Выплюнуть» шарик можно между любыми двумя шариками (а также перед первым шариком или после последнего), тогда выплевываемый шарик вставляется между этими шариками, и все шарики, которые находятся правее вставляемого, сдвигаются вправо.

В устройство может быть одновременно засосано больше одного шарика, при этом при выплевывании шарика первым выплевывается последний засосанный шарик, затем - предпоследний и т.д. (т.е. устройство работает по принципу стека). Шарики выплевываются по одному, т.е. можно выплюнуть только один шарик, остальные оставив внутри устройства (при этом дальше можно как продолжать «выплевывать» шарики в том же или в другом месте, так и засасывать новые шарики).

Наиболее энергоемкой из описанных операций является операция засасывания шарика, поэтому хочется минимизировать количество именно таких операций.

Напишите программу, которая по данному начальному расположению шариков определит минимальное количество операций засасывания, которое нужно, чтобы расположить шарики в порядке их номеров.

На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.

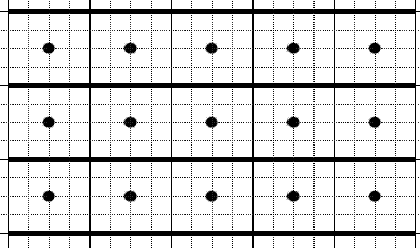
На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.

Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).

В Тридевятом Царстве было N городов, некоторые из которых были соединены дорогами. К сожалению, в последнее время добраться из одного города в другой стало очень сложно из-за возникших автомобильных пробок. В целях борьбы с пробками было решено все дороги сделать односторонними, т.е. разрешить проезд по каждой дороге только в одном направлении. При этом требуется, чтобы по-прежнему можно было из любого города попасть в любой другой.

Вася и Петя играют в следующую игру. Они берут колоду из 36 карточек. На каждой карточке написано число от 1 до 9 и каждая карточка покрашена в один из 4 цветов так, что есть ровно по 9 карточек каждого цвета и они пронумерованы числами от 1 до 9. Карты перемешиваются, и игрокам раздается по 18 карт.

Дальше игроки по очереди делают ходы. За один ход игрок может выложить на стол одну карточку по следующим правилам. Карточку с цифрой 5 можно выкладывать на стол в любой момент. Карточку с другой цифрой можно выкладывать только если на стол уже выложена карточка того же цвета, на которой написано число на 1 большее или на 1 меньшее, чем на данной карточке (не важно, была ли эта карточка выложена вами или вашим противником, и была ли она выложена на предыдущем ходе или раньше). Если игрок может выложить хоть какую-то карточку, он обязан делать ход. Если ни одну карточку игрок выложить не может, он пропускает ход.

Выигрывает тот, кто первым выложит все свои карточки на стол.

Напишите программу, которая по информации о том, кому какие карточки достались, определяет, кто выиграет при оптимальной игре обоих игроков.