На Международной олимпиаде по информатике некоторые участники, конечно же, получают удовольствие именно от решения предложенных задач, но большинство — от полученных в новой стране впечатлений. Впечатления принято запечатлевать на фотоаппарат. Участник T решил подойти к процессу съёмок с научной (по его мнению) точки зрения. Он желает заснять сразу два интересных объекта, местоположение каждого из которых на земле мы будем описывать с помощью отрезка. T выбирает точку для съёмок так, чтобы площадь двух треугольников, образованных концами соответствующих отрезков и выбранной точкой была одинаковой. Треугольники при этом должны быть невырожденными.
Помогите T с выбором такой точки. Возможность заснять сразу два объекта при этом анализировать не нужно, мы лишь действуем в рамках модели, сформулированной T. Задача упрощается тем, что каждый из отрезков, описывающих объекты, оказался параллельным одной из осей координат (возможно, каждый своей).
В первой строке входного файла находятся 4 целых числа x1, y1, x2, y2, характеризующие координаты концов первого отрезка. Во второй строке — x3, y3, x4, y4, описывающие второй отрезок. Все координаты по модулю не превосходят 1000. Каждый отрезок параллелен одной из осей координат. То есть гарантируется, что у каждого отрезка или координаты x его концов или координаты y концов совпадают. Также гарантируется, что отрезки невырождены, и что они не имеют общих внутренних точек и могут касаться только своими концами.
Если точку, удовлетворяющую условию задачи, и координаты которой по абсолютной величине не превосходят 5000 найти можно, то в первой строке выведите слово «YES». В этом случае во второй строке выведите координаты найденной точки. Если таких точек несколько, то выведите любую из них. Координаты могут оказаться вещественными, и их следует выводить с как можно бóльшим числом знаков после десятичной точки. Разница соответствующих площадей должна быть не больше 10 - 3. Площадь каждого треугольника должна быть не меньше 0.1.
Если искомую точку найти невозможно, или координаты любой такой точки по модулю превышают 5000, то выведите только слово «NO».
0 0 0 4
5 2 5 3
YES
1.00000000000000 0.0000000000000000
1 0 3 0
1 0 1 1
YES
3.00000000000 1.000000000000000
Командная олимпиада, о которой идёт речь в этой задаче, проходила по правилам, похожим на правила олимпиады, в которой вы сейчас участвуете. Отличие было только в одном: при ранжировании команд не учитывается штрафное время. При этом в случае равного количества решённых задач выше в таблице располагается та команда, чьё имя следует раньше в лексикографическом порядке.
Как и сегодня, за час до окончания олимпиады таблица результатов была «заморожена». Каково же было удивление участников, когда при подведении итогов выяснилось, что в окончательной таблице все команды расположились строго в обратном порядке, по отношению к порядку, зафиксированному «заморозкой». Так как в окончательной таблице результатов результаты сдачи каждой из задач участниками не отражены, то вам предлагается определить, могло ли такое быть в принципе, или это результат технического сбоя системы.
Первая строка содержит два натуральных числа: N — количество команд и K — количество задач (1 ≤ N, K ≤ 100).
Далее следуют N строк, описывающих саму таблицу на момент заморозки. i-я строка содержит название команды (строка из строчных латинских символов длины не более 50) и строку длины K из символов ‘ + ’ и ‘ - ’, показывающих успех команды по каждой из задач.
Команды упорядочены от первого места на момент заморозки к последнему.
Гарантируется, что никакие две команды не имеют одинаковое название.
Если порядок команд теоретически мог измениться за последний час соревнований на обратный, то сначала выведите строку «Possible», а затем таблицу окончательных результатов в формате, аналогичном таблице из входного файла (см. пример). Если соревнование так закончиться не могло, то выведите единственную строку «Impossible».
3 4
winner +-++
middle +--+
looser ----
Possible
looser ++++
middle ++-+
winner +-++
3 4
first +-++
second +--+
third ----
Impossible
Спортивный программист для достижения вершин своего мастерства должен быть натренирован в совершенно разных аспектах, в том числе и физически. Кто-то для этого садится на велосипед, кто-то ныряет в бассейн, а молодой программист Влад бегает по стадиону. Но из-за неаккуратного обращения с личными вещами его секундомер может измерять время только в минутах, без указания секунд и тем более их долей. Причём, если секундомер показывает, например, 1, то это может обозначать и время ровно 2 минуты, так как 1.(9) = 2.
Чтобы следить за прогрессом своего ученика, тренеру Влада приходится довольствоваться показаниями этого прибора. Каждый раз, когда Влад пробегает мимо тренера, сделав очередной круг по стадиону, тот записывает в блокнот показания секундомера в минутах. Первый раз тренер записывает время в момент, когда Влад пробежал первый круг. Фактически показания секундомера соответствуют целому числу минут, прошедших к определенному моменту времени.
На контрольной тренировке Влад бегал с постоянной скоростью, однако по записям тренера не так легко сказать, с какой именно. Напишите программу, которая поможет тренеру определить за какое минимальное, а также максимальное возможное время Влад мог пробегать каждый круг. Известно, что Влад начал бегать в момент времени 0 в том месте, где стоит тренер.
В первой строке входного файла находится единственное натуральное число N — количество записей в блокноте тренера (2 ≤ N ≤ 105). В следующей строке находятся сами эти записи — разделённые пробелами целые числа a1, a2, ..., aN (0 ≤ a1 ≤ a2 ≤ ... ≤ aN ≤ 106).
Выведите два неотрицательных вещественных числа, разделённых пробелом, — минимальное и максимальное возможное количество минут, за которое спортсмен пробегает один круг. Ваш ответ должен отличаться от правильного менее чем на 10 - 3.
Если ответа не существует, то есть спортсмен не мог бежать с постоянной скоростью так, чтобы записи тренера получились именно такими, в единственной строке выведите «No solution».
4
1 3 4 6
1.5 1.666666667
4
0 0 0 0
0 0.25
5
2 4 5 7 9
2 2
3
1 5 7
No solution
Во втором примере минимальное время может быть как угодно маленьким, и ответ 0 по сути это символизирует, но можно также считать, что Влад просто стоял на месте. Максимальный ответ в этом тесте соответствует реальным показаниям секундомера 0.25, 0.5, 0.75, 0.(9).
Как вы помните, Джонни работает в министерстве финансов одной небольшой страны. По роду службы ему приходится инспектировать отечественные авиакомпании и изучать маршруты, которые те предлагают.
В стране есть n городов. По государственным законам авиакомпания должна предоставлять услуги двустороннего перелёта между некоторыми парами городов, причём в целях унификации и стандартизации продолжительность любого полёта должна составлять ровно один день.
Авиакомпания называется крупной, если с помощью рейсов этой компании можно добраться из любого города страны до любого другого. Крупная авиакомпания называется экономной, если при этом количество маршрутов, ею предлагаемое, минимально возможное, которое может быть у крупной компании.
Государственная антимонопольная служба возбудила расследование против крупной авиакомпании «Aero-float». Ей предъявлено обвинение в излишней неэкономности. Джонни было поручено проинспектировать «Aero-float» в целях обнаружения финансовых махинаций, но авиакомпания отказалась раскрывать полный список предоставляемых ею прямых рейсов. После продолжительных переговоров руководство компании согласилось сообщить Джонни информацию о минимально возможном количестве перелётов между каждой парой городов, если использовать только прямые рейсы «Aero-float».
Используя эту информацию, помогите Джонни установить, может ли компания «Aero-float» быть экономной или нет? Более формально, установите, существует ли набор рейсов, при котором число рейсов в кратчайших маршрутах именно такие, как было сообщено Джонни, и при котором компания является экономной?
В первой строке содержится единственное целое число n (2 ≤ n ≤ 250) — количество городов в стране.
Далее идёт n строк, содержащих по n целых чисел Ti, j: j-е число в i-й строке равняется минимальному количеству перелётов, требуемому на перемещение из i-го города в j-й.
Гарантируется, что предоставленная информация корректна, то есть существует некоторый набор рейсов, который соответствует данному набору чисел Ti, j.
Выведите «YES», если компания «Aerofloat» может являться экономной, или «NO» в противном случае.
5
0 2 1 1 1
2 0 1 3 3
1 1 0 2 2
1 3 2 0 2
1 3 2 2 0
YES
4
0 1 1 1
1 0 2 2
1 2 0 1
1 2 1 0
NO
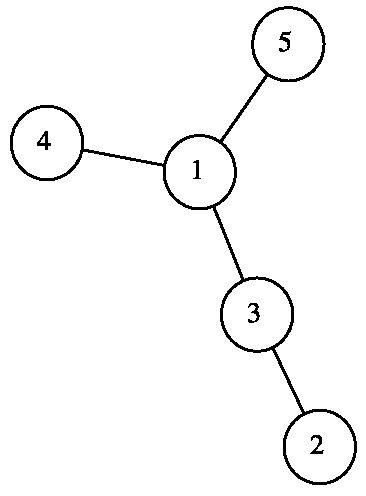
Для первого примера ниже приведён возможный вариант предлагаемых компанией маршрутов, при котором она является экономной. На рисунке соединены те пары городов, между которыми есть прямые рейсы.