Темы --> Информатика --> Язык программирования
    Процедуры и функции(96 задач)
    Массивы(232 задач)
    Типы данных(356 задач)
    Циклы(177 задач)
    Условный оператор (if)(164 задач)
    Python(260 задач)
    Standard Template Library(2 задач)
---> 22 задач <---
Источники --> Командные олимпиады --> ВКОШП
    1999(7 задач)
    2000(8 задач)
    2001(8 задач)
    2002(9 задач)
    2003(9 задач)
    2004(10 задач)
    2005(10 задач)
    2006(10 задач)
    2007(11 задач)
    2008(10 задач)
    2009(11 задач)
    2010(11 задач)
    2011(11 задач)
    2012(11 задач)
    2013(11 задач)
    2014(11 задач)
    2015(11 задач)
    2016(11 задач)
Страница: << 1 2 3 4 5 >> Отображать по:
#431
Восстановление программы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Задана последовательность команд "поворот налево" и "поворот направо". Требуется каждой команде сопоставить число шагов, чтобы путь не пересекал и не касался самого себя.

Выполняя очередное задание Министерства образования и сельского хозяйства, программисты Флатландского государственного университета информационных технологий, удобрений и ядохимикатов создали специального робота по прокладке оросительных каналов.

Программа для робота представляет собой последовательность команд. Команды робота приведены в следующей таблице:

 

Команда

Обозначение

Действия робота

Перемещение

(X)

Переместиться вперед на X километров, прокладывая за собой оросительный канал
Поворот налево L Повернуть налево на 90o
Поворот направо

R

Повернуть направо на 90o

Любая программа начинается и заканчивается командами перемещения и не содержит двух команд перемещения или двух команд поворота подряд.

Исходно робот размещается в некоторой точке поля, на котором требуется создать оросительную систему. После запуска робот последовательно выполняет команды своей программы. Программа считается корректной, если полученный в результате ее выполнения канал не имеет самопересечений или самокасаний.

Программисты университета написали программу и собрались отправить ее по электронной почте в министерство. Однако, в результате поражения сети университета вирусом программа оказалась испорчена. А именно, из нее исчезли все команды перемещения. Теперь программистам требуется восстановить программу. Поскольку времени очень мало, решено было оставить сохранившиеся команды поворота, вставив между ними команды перемещения так, чтобы получившаяся программа была корректной.

Входные данные

Входные данные содержат команды поворота исходной программы в том порядке, в котором они в ней следовали. Каждая команда представляет собой символ «L» либо «R», команды друг от друга не отделяются. Количество команд не превышает 30 000.

Выходные данные

Выведите  любую корректную программу, последовательность команд поворота в которой совпадает с последовательностью, заданной во входных данных. Параметр X каждой команды перемещения должен быть положительным целым числом и не должен превышать 109. Все команды выведите в одной строке и друг от друга не отделяйте.

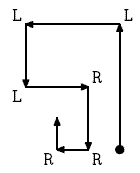
includegraphics{pics/program.1}
Примеры
Входные данные
LLLRRR
Выходные данные
(4)L(3)L(1)L(2)R(2)R(1)R(1)
#520
Упаковка
  
Источники: [ Командные олимпиады, ВКОШП, 2003, Задача E ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Даны размеры контейнера (в трех измерениях) и двух коробок. Необходимо определить, помещаются ли коробки в контейнер, если верх обязательно должен совпадать и боковые грани должны быть параллельны граням контейнера.

В одну транспортную компанию поступил заказ на перевозку двух ящиков из одного города в другой. Для перевозки ящики решено было упаковать в специальный контейнер.

Ящики и контейнер имеют вид прямоугольных параллелепипедов. Длина, ширина и высота первого ящика – \(l_1\), \(w_1\) и \(h_1\), соответствующие размеры второго ящика – \(l_2\), \(w_2\) и \(h_2\). Контейнер имеет длину, ширину и высоту \(l_c\), \(w_c\) и \(h_c\).

Поскольку ящики содержат хрупкое оборудование, после упаковки в контейнер каждый из них должен остаться в строго вертикальном положении. Таким образом, ящики можно разместить рядом или один на другом. Для надежного закрепления в контейнере стороны ящиков должны быть параллельны его сторонам. Иначе говоря, если исходно ящики были расположены так, что все их стороны параллельны соответствующим сторонам контейнера, то каждый из них разрешается перемещать и поворачивать относительно вертикальной оси на угол, кратный 90 градусам.

Разумеется, после упаковки оба ящика должны полностью находиться внутри контейнера и не должны пересекаться.

Выясните, можно ли поместить ящики в контейнер с соблюдением указанных условий.

Входные данные

Первая строка входных данных содержит \(l_1\), \(w_1\) и \(h_1\), вторая – \(l_2\), \(w_2\) и \(h_2\), третья – \(l_c\), \(w_c\) и \(h_c\). Все размеры – целые положительные числа, не превышающие 1000. Числа в строках разделены пробелами.

Выходные данные

Выведите YES, если ящики можно упаковать в контейнер, и NO в противном случае.

Пояснения к примерам

В первых двух примерах ящики можно разместить рядом, при этом во втором один из них следует повернуть на 90 градусов. В третьем примере ящики можно разместить один на другом. В четвертом примере первый ящик слишком высокий и не влезает в контейнер. В пятом примере ящики нельзя разместить ни рядом, ни один на другом.

Примеры
Входные данные
2 2 3
3 3 3
3 5 3
Выходные данные
YES
Входные данные
2 3 3
3 2 3
4 4 4
Выходные данные
YES
Входные данные
4 1 2
3 3 2
4 3 4
Выходные данные
YES
Входные данные
1 1 4
1 1 3
10 10 3
Выходные данные
NO
Входные данные
3 2 2
3 1 2
5 2 3
Выходные данные
NO
#521
Манхаттанский полицейский
  
Источники: [ Командные олимпиады, ВКОШП, 2003, Задача F ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Вершины графа находятся в точках пересечения линий сетки, а горизонтальные или вертикальные ребра единичной длины существуют только между ближайшими вершинами. Необходимо пройти по каждому ребру как минимум один раз совершив как можно меньше переходов.

Недавно Билл устроился на работу полицейским. Теперь ему предстоит каждый вечер обходить свой участок, который представляет собой прямоугольник, состоящий из N×M кварталов. Каждый квартал имеет вид квадрата размером 100×100 метров, кварталы отделены друг от друга прямыми улицами.

Таким образом, через участок Билла проходит \(N\) + 1 улица, идущая с запада на восток и \(M\) + 1 улица, идущая с севера на юг. Перекрестки разбивают улицы на (\(N\) + 1)\(M\) + (\(M\) + 1)\(N\) отрезков, каждый из которых имеет длину 100 метров.

Совершая обход, Билл выходит из полицейского управления, расположенного около юго-западного угла его участка, обходит свой участок и возвращается в управление. Во время обхода Билл должен пройти по каждому отрезку улицы на территории своего участка как минимум один раз. Известно, что во время обхода Билл проходит отрезок длиной 100 метров за одну минуту. Выясните, какое минимальное число минут потребуется Биллу, чтобы совершить обход.

Входные данные

Вводятся целые числа N и M, разделенные пробелом (1\( \le\)N, M\( \le\)10 000).

Выходные данные

Выведите минимальное время, за которое Билл может совершить обход.

Пояснение ко второму примеру

Один из возможных оптимальных путей для Билла во втором примере показан на рисунке.

Примеры
Входные данные
1 1
Выходные данные
4
Входные данные
2 2
Выходные данные
16
Входные данные
3 4
Выходные данные
38
#536
Монстры
  
Источники: [ Командные олимпиады, ВКОШП, 2002, Задача A ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На прямоугольной таблице находятся монстры. Каждый монстр характеризуется координатами и направлением движения. Монстр идет до конца поля и оставляет следы. Необходимо определить суммарное количество испачканных клеток.

В одной секретной лаборатории вывели новый вид маленьких монстров, размером чуть больше суслика. В ходе исследований ученые решили поставить следующий эксперимент. В центре комнаты устанавливается прямоугольный стол, поверхность которого разбита на \(N\) х \(M\) клеток размера 1 х 1. В начальный момент времени на некоторых его клетках располагаются монстры, смотрящие параллельно сторонам стола. По команде экспериментатора монстры начинают двигаться по прямой в ту сторону, в которую они смотрят, доходят до края стола и спрыгивают на пол. Там их собирает лаборант Петя и относит в клетку.

Поскольку у монстров очень грязные лапки, они оставляют следы на тех клетках, на которых они побывали. Так как отмывать стол придется лаборанту Пете, его заинтересовал вопрос - в каком количестве клеток побывают монстры. Помогите ему решить эту сложную задачу.

Входные данные

В первой строке вводятся числа \(M\) и \(N\) - размеры лабораторного стола (1 <= \(M\), N <= \(10^6\)). В следующей строке задается число \(K\) - количество монстров (0 <= \(K\) <= \(10^3\)). Следующие \(K\) строк содержат описания монстров - два целых числа и один символ из множества {\(N\), \(E\), \(S\), \(W\)} - начальные координаты и направление соответствующего монстра (соответствие направлений и координат приведено на рисунке 1). Символ отделен от чисел ровно одним пробелом.

Выходные данные

Выведите единственное число - количество клеток стола, на которых побывают монстры.

Пояснение к примеру

Пример соответствует расположению монстров, приведенному на рисунке 1.монстры.

Примеры
Входные данные
8 5
4
4 4 S
6 2 W
6 3 N
6 4 S
Выходные данные
13
#541
Столица
  
Источники: [ Командные олимпиады, ВКОШП, 2002, Задача F ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Задана таблица, некоторые клетки содержат города. Расстояние между городами определяется как |x1 - x2| + |y1 - y2|. Требуется выбрать место для столицы так, чтобы суммарное расстояние до всех городов было минимальным. Столица не должна совпадать с существующим городом.

В некотором царстве, в некотором государстве было \(N\) городов, и все они, судя по главной карте императора, имели целые координаты. В те годы леса были дремучие, дороги же строить умели только параллельно осям координат, так что расстояние между двумя городами определялось как |\(x_1\) - \(x_2\)| + |\(y_1\) - \(y_2\)|.

Император решил построить \(N\)+1-ый город и сделать его столицей своего государства, при этом координаты столицы также должны быть целыми. Место для столицы следует выбрать так, чтобы среднее арифметическое расстояний между столицей и остальными городами было как можно меньше. Однако, разумеется, столицу нельзя строить на месте существующего города.

Нелегкая задача выбрать место для столицы поручена Вам.

Входные данные

В первой строке вводится число \(N\) - количество городов (1 <= \(N\) <= 100). Следующие \(N\) строк содержат координаты городов - пары целых чисел, не превышающих 1000 по абсолютной величине.

Выходные данные

Выведите два целых числа - координаты точки, где следует построить столицу. Если решений несколько, выведите любое.

Примеры
Входные данные
8
0 0
1 0
2 0
0 1
2 1
0 2
1 2
2 2
Выходные данные
1 1
Входные данные
4
0 0
1 1
0 1
1 0
Выходные данные
0 -1
Страница: << 1 2 3 4 5 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест