Страница: << 1 2 3 Отображать по:

#2979

Скоростной диаметр для кольцевой дороги

Темы: [Элементарная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2010, Задача H ]

Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.

После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.

Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы $d$ километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно $d$.

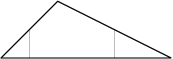
Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.

Входные данные

Первая строка входного файла содержит два целых числа $n$ — количество вершин у многоугольника, задающего кольцевую автодорогу ($3 \le n \le 100000$), и $d$ — длину новой магистрали ($1 \le d \le 10^8$).

Далее следует описание расположения вершин — каждая из следующих $n$ строк содержит координаты $x$ и $y$ ($-10^8 \le x, y \le 10^8$) соответствующей вершины. Вершины заданы в порядке их обхода против часовой стрелки.

Направлению с севера на юг соответствуют прямые, задаваемые уравнением $x = c$ для некоторого $c$. Заданный многоугольник является монотонным.

Выходные данные

В выходной файл выведите количество способов построить дополнительную магистраль длиной ровно $d$. Если способов постройки бесконечно много, выведите в выходной файл «Infinity».

#111828

Швабра

Темы: [Вычислительная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача J ]

Первокурсник Рома приехал в общежитие и, удивившись беспорядку в комнате и толстому слою пыли на полу, начал наводить порядок. Первым делом он решил вымыть пол. Для этого Рома в магазине приобрел инновационную швабру.

Изначально моющая часть швабры имела идеальную прямоугольную форму, но в процессе перевозки из магазина в общежитие у нее отломился один из углов. Таким образом, теперь она представляет собой многоугольник, граница которого состоит из двух соседних сторон прямоугольника, фрагментов двух оставшихся сторон и ломаной, соединяющей концы этих фрагментов.

$\text{[math]}$

Рома живет в большой прямоугольной комнате. Рома провел сломанной шваброй от одной стороны комнаты до другой, не отрывая ее от стены, так что в результате отломанный угол швабры оказался в углу комнаты. При этом часть соответствующей прямоугольной полосы пола в углу осталась невымытой.

$\text{[math]}$

Рома считает, что все точки, в которых в какой-то момент находилась моющая часть швабры оказались вымыты. Теперь он решил выяснить, какая часть этой полосы осталась грязной.

$\text{[math]}$

Помогите ему вычислить площадь этой части. Можете считать, что размер комнаты, в которой живет Рома, существенно больше размеров моющей части швабры.

Формат входного файла

Первая строка входного файла содержит два целых числа $w$ и $h$ - размеры моющей части швабры до повреждения ($2 \le w, h \le 10^5$).

Вторая строка содержит целое число $n$ - число вершин ломаной, соединяющей соседние стороны швабры ($2 \le n \le 10^5$). В $i$-й из следующих $n$ строк заданы два целых числа $x_i$ и $y_i$ ($1 \le x_i < w$, $1 \le y_i < h$, за исключением $y_1 = h$, $x_n = w$) - координаты $i$-й вершины ломаной. Ломаная не имеет самопересечений и самокасаний.

Координаты введены таким образом, что стена, вдоль которой Рома провел шваброй, соответствует прямой $y=h$.

Формат выходного файла

В выходной файл выведите площадь невымытой части пола с абсолютной или относительной погрешностью не более $10^{-6}$. Это значит, что если правильный ответ $a$, а вы вывели $p$, то ваш ответ будет засчитан как правильный, если $\frac{|a-p|}{\max(|a|, 1)}\le 10^{-6}$.

Примеры

Входные данные

Выходные данные

18.0

Страница: << 1 2 3 Отображать по:

Выбрано

Отменить

Добавить в контест