Фирма Julick&Co ведет учет своих доходов и расходов. Но главный бухгалтер этой фирмы не любит математику, поэтому всякую сумму денег, которую фирма получает или отдает, он характеризует некоторым признаком. Например, сумму денег от 5 до 10 рублей он может охарактеризовать словом "МАЛО", а от 7 до 60 рублей словом "МНОГО". Время от времени он пересчитывает деньги и записывает признак суммы, которая имеется у фирмы. Недавно налоговая инспекция заинтересовалась доходами данной организации. Она хочет узнать, какая минимальная и максимальная сумма денег может быть сейчас у этой фирмы или выяснить, что имеется ошибка в ее записях. Известно, что по законам страны, где развиваются события, в любой момент времени организация должна обладать неотрицательной суммой денег.
Первая строка входного файла содержит \(K\) (\(1 \leq K \leq 100\)) – количество признаков, которые бухгалтер использует для описания различных сумм денег. На следующих \(K\) строках содержатся соответствующие признаки \(S_i\) и числа \(Min_i\) и \(Max_i\). \(S_i\) - слово, состоящие не более чем из \(20\) латинских букв, отделенное от последующих чисел одним пробелом, \(Min_i\) и \(Max_i\) - целые положительные числа (\(1 \leq Min_i \leq Max_i \leq 1000\)), разделенные одним пробелом. Следующая строка содержит количество денег, которое было у фирмы в начале ее деятельности – целое число . Затем следует число \(N\) – количество записей в бухгалтерской книге фирмы Julick&Co (\(1 \leq N \leq 100\)). Следующие N строк содержат записи в следующем формате: первый символ строки из множества {"+", "-", "!"} означает вид операции – доход, расход или подсчет денег соответственно. Непосредственно за этим символом (без пробелов) следует признак, характеризующий сумму денег, использованную в операции.
Если в учетных записях содержится ошибка, выведите в выходной файл число \(-1\), в противном случае выведите числа \(Min\) и \(Max\) - наименьшую и наибольшую сумму денег, которая может быть у фирмы Julick&Co.
3 LITTLE 1 5 MIDDLE 4 10 BIG 18 50 11 3 +MIDDLE !BIG -LITTLE
13 20
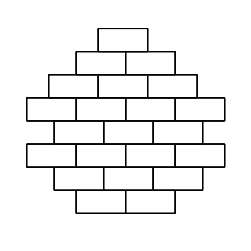
Воодушевленный легендой о Вавилонской Башне, Петя решил построить ее аналог у себя в комнате, для этого он взял \(N\) детских строительных кирпичиков, выбрал для себя размер основания \(D\) и высоту башни \(H\). Кроме того, он решил для себя, что размер каждого следующего уровня будет отличаться от предыдущего на один. Башня, показанная на рисунке, удовлетворяет Петиным запросам, имеет основание \(2\), высоту \(8\), и составлена из \(22\) кирпичиков.
Ваша задача состоит в том, чтобы написать программу, которая определяет, можно ли построить башню при выбранных Петей параметрах, и если да, то выдает сколько кирпичей должно быть на каждом уровне.
Во входном файле находятся числа \(N\), \(D\), и \(H\), разделенные пробелами (\(1 \leq N \leq 1000\), \(1 \leq D,H \leq 30\)).
Если башня, удовлетворяющая Петиным запросам существует, выведите в выходной файл \(N\) чисел – проект любой такой башни – количество кирпичиков на каждом уровне, начиная с самого нижнего. В противном случае выведите \(0\).
22 2 8
2 3 4 3 4 3 2 1