На планете Плюк, поверхность которой мы будем считать абсолютно плоской, был разработан новый принцип перемещения единственного имеющегося там транспортного средства – пепелаца. А именно, на расстоянии одного километра друг от друга в точках (0, 0) и (1, 0) были построены две станции управления пепелацами A и B. С помощью них можно мгновенно переместить любой пепелац, повернув его на 90 градусов по или против часовой стрелки относительно точки A или B. Расстояние от пепелаца до соответствующей станции при этом не меняется. Следующее перемещение можно делать как относительно той же станции, так и относительно другой.
Например, если повернуть пепелац, находящийся в точке (3, 1) на 90 градусов против часовой стрелки относительно станции A, то он переместится в точку (- 1, 3), если его затем повернуть на 90 градусов по часовой стрелке относительно станции B, то он переместится в точку (4, 2), если затем повернуть его вокруг станции B по часовой стрелке еще раз, он переместиться в точку (3, - 3).
Один житель планеты недавно решил отправиться на своем пепелаце в гости к другу. Житель проживает около точки с координатами (x1, y1), а его друг – около точки с координатами (x2, y2). Помогите жителю с помощью станций управления пепелацем оказаться как можно ближе к месту, где проживает его друг, чтобы потом меньше было идти по пустыне.
Поскольку перемещения мгновенные и абсолютно бесплатные, то минимизировать количество перемещений не надо.
На вход программы поступают четыре целых числа – x1, y1, x2 и y2, они не превышают 104 по абсолютной величине.
Выведите последовательность перемещений с использованием станций управления, которая перемещает пепелац из точки (x1, y1) как можно ближе к точке (x2, y2).
Поворот по часовой стрелке относительно станции A обозначается как «+A», поворот против часовой стрелки относительно станции A обозначается как «-A», соответствующие повороты относительно станции B обозначаются как «+B» и «-B». Выводите по одному перемещению на строке.
Выведенная последовательность не обязана быть минимальной по количеству перемещений, но должна содержать не более 106 действий.
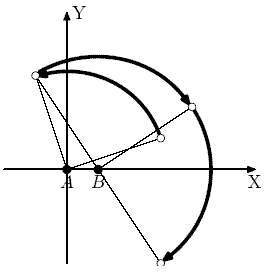
3 1 3 -3
+A -B -B +A +A -B -B +A
0 0 3 0
-A +B +A -B
Одной из первоочередных задач, стоящих перед министерством обороны Флатландии, является модернизация вооружения. В связи с этим было решено построить новый испытательный полигон.
По форме полигон представляет собой выпуклый многоугольник. Для демонстрации военных испытаний на полигоне различным чиновникам, неподалеку от него решено было построить наблюдательный центр. В результате длительных исследований было установлено, что основной характеристикой местоположения наблюдательного центра является степень этого центра относительно полигона.
Степень точки A относительно многоугольника вычисляется по следующему правилу. Рассмотрим все лучи с вершиной в точке A, имеющие общие точки с многоугольником. Для каждого такого луча найдем минимальное и максимальное расстояние вдоль него от точки A до некоторой точки многоугольника: dmin и dmax. Степенью точки относительно данного многоугольника назовем минимум величины dmin×dmax по всем таким лучам.
Военные не справляются с задачей вычисления степени наблюдательного центра относительно полигона и решили подключить к этой задаче вас. Помогите им!
Будем считать, что наблюдательный центр находится в точке (0, 0). На вход программы поступает описание полигона.
В первой строке вводится число n – количество вершин полигона ( 3
n100). Следующие n строк содержат по два вещественных числа – координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают 1000 по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
Выведите одно число – степень наблюдательного центра относительно полигона. Ответ должен отличаться от правильного не более чем на 10-4.
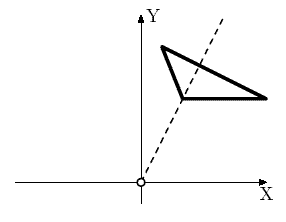
3 1.0 2.0 3.0 2.0 0.5 3.25
7.0000000000
Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.
Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
- если вершина красная, то ее родитель – черный;
- количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.
 |
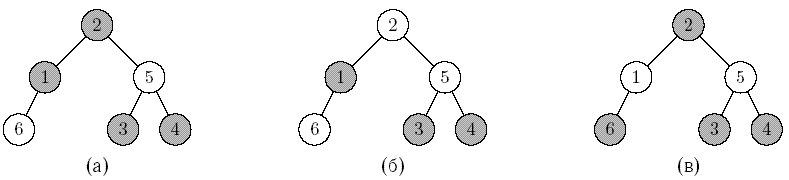Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.
Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.
В первой строке вводится число n – количество вершин в дереве ( 1n1000).
Пусть вершины дерева пронумерованы числами от 1 до n. Следующие n строк содержат по два числа – для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор вводимых чисел действительно задает двоичное дерево.
Выведите одно число – количество способов раскрасить вершины заданного двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.
 |
6 6 0 1 5 0 0 0 0 3 4 0 0
3
4 2 0 3 0 4 0 0 0
0
Максимальное время работы на одном тесте: 2 секунды
При разработке программ для просмотра веб-страниц одной из наиболее сложных задач является корректное отображение таблиц. Компания «Kozilla», в которой вы работаете, планирует разработать новую версию браузера «Waterrat» для работы в терминальном режиме и просит вас написать фрагмент ядра отображения веб-страниц, ответственный за формирование структуры таблиц.
Фрагмент, который вы должны написать, получает на вход информацию о количестве строк таблицы и ячейках этих строк и должен сгенерировать структуру таблицы и передать ее модулю, который занимается отображением таблицы на экране.
Таблица состоит из строк, каждая строка состоит из одной или нескольких ячеек, j-я ячейка i-й строки имеет ширину ai, j.
По заданным параметрам таблицы постройте символическое изображение ее структуры.
В первой строке вводится число n – количество строк в таблице ( 1n100). Каждая из следующих n строк входных данных описывает одну строку таблицы.
Описание строки включает число mi – количество ячеек в этой строке, и mi целых чисел ai, 1, ai, 2,..., ai, mi – ширину каждой из ячеек строки ( 1mi10, 1ai, j20).
Выведите символическое изображение структуры таблицы.
Изображение i-й строки таблицы должно начинаться горизонтальной линией, составленной из символов «+» (плюс) и «-» (минус). Затем должна следовать строка, содержащая пробелы и символы «|» (вертикальная черта). Первым символом строки должна быть вертикальная черта, затем ai, 1 пробелов, затем вертикальная черта, затем ai, 2 пробелов, и так далее, всего mi блоков пробелов. После последнего блока должна следовать вертикальная черта.
После последней строки таблицы также должна следовать горизонтальная линия.
В изображении горизонтальной линии используйте символ «+», если сверху или снизу от этой позиции находится вертикальная черта, и «-» в противном случае. Горизонтальная черта должна иметь минимальную возможную длину, чтобы над каждым символом вертикальной черты следующей строки и под каждым символом вертикальной черты предыдущей строки были символы «+».
4 3 3 5 1 1 2 1 2 2 5 1
+---+-----+-+ | | | | +--++-----+-+ | | +--+ | | +--+--+-+ | | | +-----+-+
Ребята во дворе решили поиграть в прятки. Чтобы выбрать ведущего, который будет искать, они решили воспользоваться считалкой. Считалка состоит из k слов и используется следующим образом.
Все n ребят становятся в круг, и один из них, начиная с себя, по очереди указывает на ребят в порядке, в котором они стоят по кругу, называя слова считалки. Тот, на кого указывает считающий, называя последнее слово считалки, выбывает из круга. После этого считалка повторяется сначала, а счет начинается со следующего за выбывшим. Так продолжается до тех пор, пока в круге не останется один человек. Он то и будет ведущим.
Но на этот раз ребята так увлеклись идеей предстоящей игры, что забывали выходить из круга после того, как считающий указывал на них, называя последнее слово считалки. В результате считающий снова указывал на них при следующих повторениях считалки.
Ребята заметили это только тогда, когда после очередного повторения считалки считающий снова указал на последнем слове на участника, который уже должен был покинуть круг. Теперь их заинтересовал вопрос – а на скольких ребят в этот момент считающий все еще не указал, что они должны покинуть круг.
Помогите им ответить на этот вопрос.
Вводятся два целых числа – n и k ( 1n1000, 1k109).
Выведите одно число – количество ребят, на которых ведущий еще не указал, что они должны покинуть круг, когда ведущий повторно укажет на кого-либо на последнем слове считалки.
6 14
3
6 13
0