Будущие программисты Андрей и Борис вчера впервые поехали кататься с родителями по новой кольцевой дороге. Каждый из них выехал на дорогу в определённом месте, сделал полный круг и вернулся домой. От скуки они оба считали фонарные столбы, расположенные посередине дороги между встречными полосами движения, так что все N фонарных столбов у каждого из мальчиков получили номера от 1 до N . Но само значение N они не запомнили. При этом два столба обоим мальчикам запомнились особенно: на одном из них висел яркий плакат ко Дню города, а на другом — флаг Москвы. Каждый из мальчиков записал себе в тетрадку номер каждого из этих двух столбов.
Сегодня обе семьи, Андрея и Бориса, пошли на выставку кошек, и там мальчики, обсудив свои поездки, задались вопросом: сколько же всего фонарных столбов на новой кольцевой дороге? Единственное, что они смогли выяснить, в одном ли направлении ехали они по дороге.
Так сложилось, что Андрей — ваш младший брат, поэтому именно вам предстоит ответить на вопрос мальчиков. У вас есть серьёзное подозрение, что может не получиться однозначно найти ответ, а мальчики боятся больших чисел, поэтому вы решили сказать им лишь минимальное из возможных значений числа N .
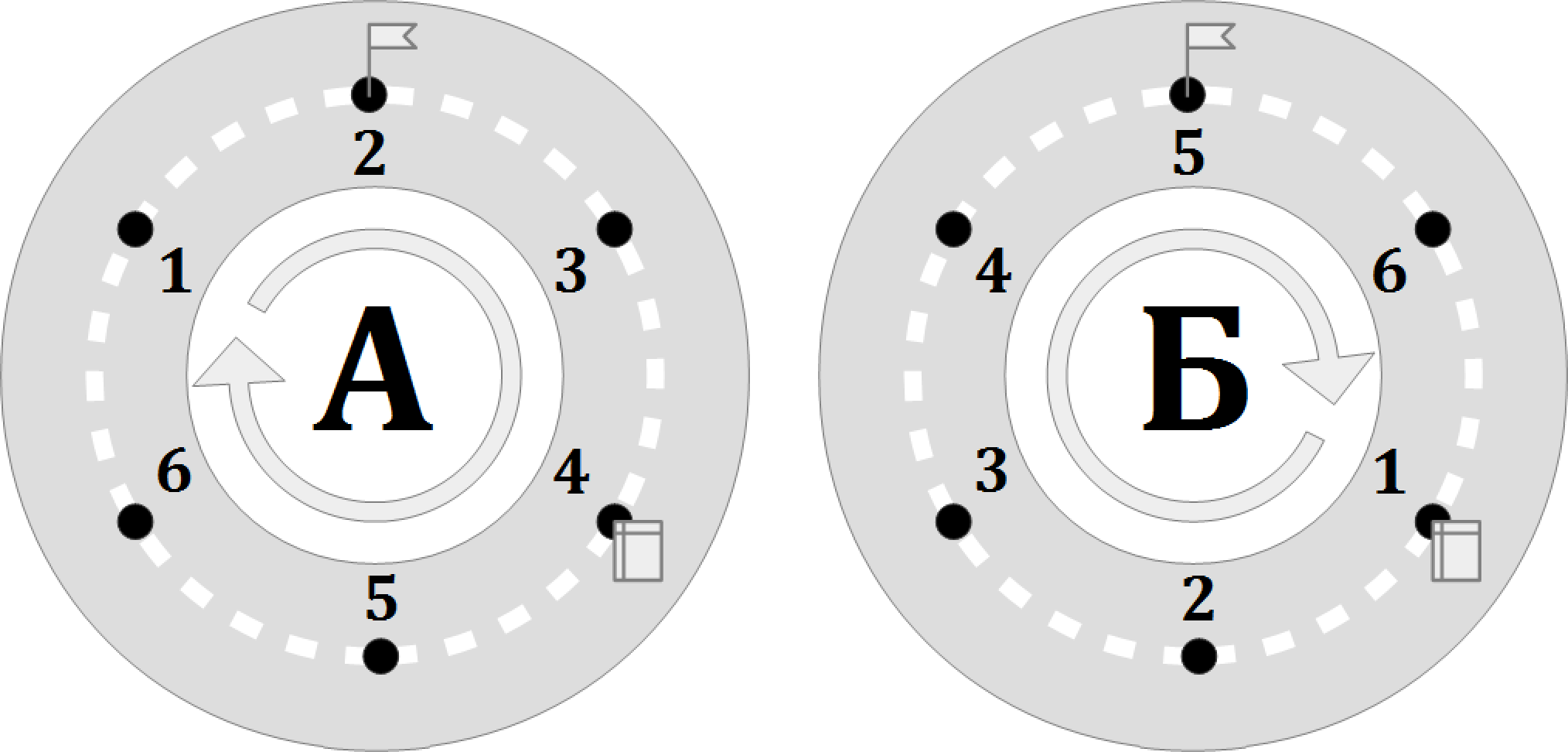
В этом примере N = 6 , A p = 4 , A f = 2 , B p = 1 , B f = 5 .
Первая строка ввода содержит единственное целое число D , которое равно 1 , если мальчики ехали в одном направлении, и - 1 , если в разных. Следующие 4 строки содержат 4 натуральных числа A p , B p , A f , B f , по одному числу в строке, каждое из которых не превосходит 10 6 : A p — номер столба с плакатом в нумерации Андрея, B p — номер этого столба в нумерации Бориса, A f — номер столба с флагом в нумерации Андрея, B f — номер этого столба в нумерации Бориса.
Плакат и флаг могли оказаться на одном столбе — в этом случае каждый из мальчиков должен был бы получить два одинаковых числа, т. е. A p = A f и B p = B f .
Выведите единственное натуральное число N — минимально возможное количество столбов. Если мальчики где-то ошиблись, и таких чисел, как у них, не могло получиться ни при каком зна-че-нии N , выведите число - 1 .
1 4 1 2 5
6
-1 4 9 4 7
-1
Команда туристического клуба «В гору пойдёт!» только что вернулась из очередного похода. Прямо сейчас участники экспедиции с жаром спорят о том, какой же горный хребет они покорили.
Достоверно известно, что на маршруте было N стоянок, причём все — на разной целочисленной высоте от 1 до N над уровнем моря. Альпинисты заблаговременно прибыли на место первой стоянки, а потом шли по маршруту в течении N - 1 дня: в первый день они шли от 1 -й стоянки до 2 -й, во второй — от 2 -й до 3 -й и так далее, пока в последний день не совершили переход от стоянки под номером N - 1 до стоянки под номером N , завершив этим свой маршрут.
Участники экспедиции пытаются понять, на какой высоте находилась каждая стоянка. В их распоряжении имеется запись в журнале, содержащая информацию о том, сколько дней они шли в гору, а сколько — спускались.
Помогите альпинистам! Подскажите им хоть какой-нибудь вариант маршрута, не противоречащий записи в журнале.
Входные данные содержат две строки. В первой строке записано целое неотрицательное число A — это количество дней, в которые альпинисты поднимались в гору. Вторая строка содержит целое неотрицательное число B — количество дней, в которые альпинисты спускались ( A + B + 1 = N , 1 ≤ N ≤ 100 000 ).
Выведите N различных целых чисел от 1 до N , разделённых пробелами, — маршрут, по которому могли пройти альпинисты. Маршрут описывается высотами стоянок в том порядке, в котором их могли посетить участники экспедиции.
0 1
2 1
3 0
1 2 3 4
Что может быть проще простого числа? Казалось бы, объяснить, что такое простое число, можно даже человеку, совершенно далёкому от математики: целое число называется простым , если оно не меньше двух и не делится ни на какое целое положительное число, кроме единицы и самого себя. Это определение будет понятно даже третьекласснику, только-только познакомившемуся с делением. Что может быть проще? Но, как часто случается в математике, за кажущейся простотой определения скрывается очень глубокая теория с множеством нетривиальных фактов, многие из которых остаются недоказанными и по сей день.
Леопольд очень интересуется всем, что связано с простыми числами. Недавно он узнал про Постулат Бертрана — оказывается, на отрезке между N и 2 N всегда найдётся хотя бы одно простое число! Несмотря на простую формулировку и интуитивную очевидность этого утверждения, сформулированного французским математиком Жозефом Луи Франсуа Бертраном, оно было доказано только в середине 19 века русским математиком Пафнутием Львовичем Чебышёвым.
Впечатлённый тем, как можно увековечить своя имя на страницах истории математики, Леопольд решил выдвинуть какую-нибудь не менее важную и серьёзную гипотезу, а потом доказать её, и назвать полученный факт теоремой Леопольда. Для этого ему нужна помощь в отыскании закономерностей, описывающих простые числа. Он просит вас написать для него программу, которая ищет отрезок из L последовательных натуральных чисел, содержащий ровно K простых чисел. Чтобы результаты было легче анализировать, он просит вас ограничиться в поисках первыми тридцатью тысячами натуральных чисел. Помогите ему, и, возможно, и вам удастся оставить след в истории!
На вход программе подаются целые числа L и K ( 1 ≤ L ≤ 30 000, 0 ≤ K ≤ L ), каждое в отдельной строке.
Если в пределах до 30 000 найдётся отрезок из L подряд идущих натуральных чисел, среди которых ровно K простых, выведите минимальное и максимальное число на этом отрезке. В противном случае выведите единственное число - 1 . Если существует несколько отрезков, удовлетворяющих условию, выведите любой.
20 5
8 27
100 66
-1
Склад завода по изготовлению матрёшек переполнен! Нужно как-то освобождать место, поэтому директор завода принял волевое решение продать абсолютно всё, что там лежит. Больше всего места на складе занимают заготовки для матрёшек — нераскрашенные статуэтки целых положительных размеров, которые можно вставлять друг в друга, если размер одной меньше чем размер другой. Увы, в таком неприглядном виде покупать их никто не хочет.
К счастью, завод сотрудничает с союзом художников по матрёшкам. В частности, был заключён договор, позволяющий заводу заказывать роспись матрёшек. В договоре указано, что матрёшка — это упорядоченный набор из M статуэток ( 1 ≤ M ) размеров r 1 < r 2 < r 3 < ... < r M . Там же прописано, что стоимость раскрашивания одной матрёшки равна одному тугрику, при этом количество статуэток, входящих в матрёшку, значения не имеет.
Получается, что для того чтобы продать всё содержимое склада, нужно сначала собрать заготовки в матрёшки и заказать роспись полученных матрёшек у художников. Помогите директору завода сделать это, потратив как можно меньше тугриков!
В первой строке входных данных содержится число N — количество заготовок на складе ( 1 ≤ N ≤ 1 000 ). В последующих N строках содержатся целые числа s 1 , s 2 , s 3 , ..., s N , где s i — это размер i -й заготовки ( 1 ≤ s i ≤ 1 000 ).
В первой строке выходного файла выведите целое число T — минимальное количество тугриков, которое нужно заплатить художникам.
Далее выведите T строк, описывающие матрёшек, которые завод закажет у союза художников. Матрёшка описывается возрастающей последовательностью чисел r 1 , r 2 , r 3 , ..., r M , где r i — размер i -й заготовки, входящей в матрёшку.
5 1 3 2 2 3
2 1 2 3 2 3
6 4 2 1 2 4 2
3 1 2 4 2 4 2
В одном уездном городе Эн было решено построить собственное метро. Все силы города были мобилизованы на выкапывание станций и прокладку подземных путей дедовскими лопатами.
Вся эта история нас бы совершенно не интересовала, если бы однажды в мэрию города не пришло письмо из далёкой страны Емакира. Оказалось, что компания Alpep подозревает администрацию уездного города в нарушении их патента на jMetro и грозится возбудить против города Н дело. Согласно патенту, jMetro — это метро, в котором:
- существует ровно одна узловая станция, в которой начинаются все радиальные линии метро, и это единственная станция, принадлежащая хотя бы двум радиальным линиям;
- количество радиальных линий не меньше пяти;
- существует ровно одна кольцевая линия, все станции которой лежат на радиальных линиях, причём на каждой радиальной линии лежит ровно одна станция кольцевой линии;
- кольцевая линия не проходит через узловую станцию;
- кольцевая линия не проходит через конечные станции радиальных линий.
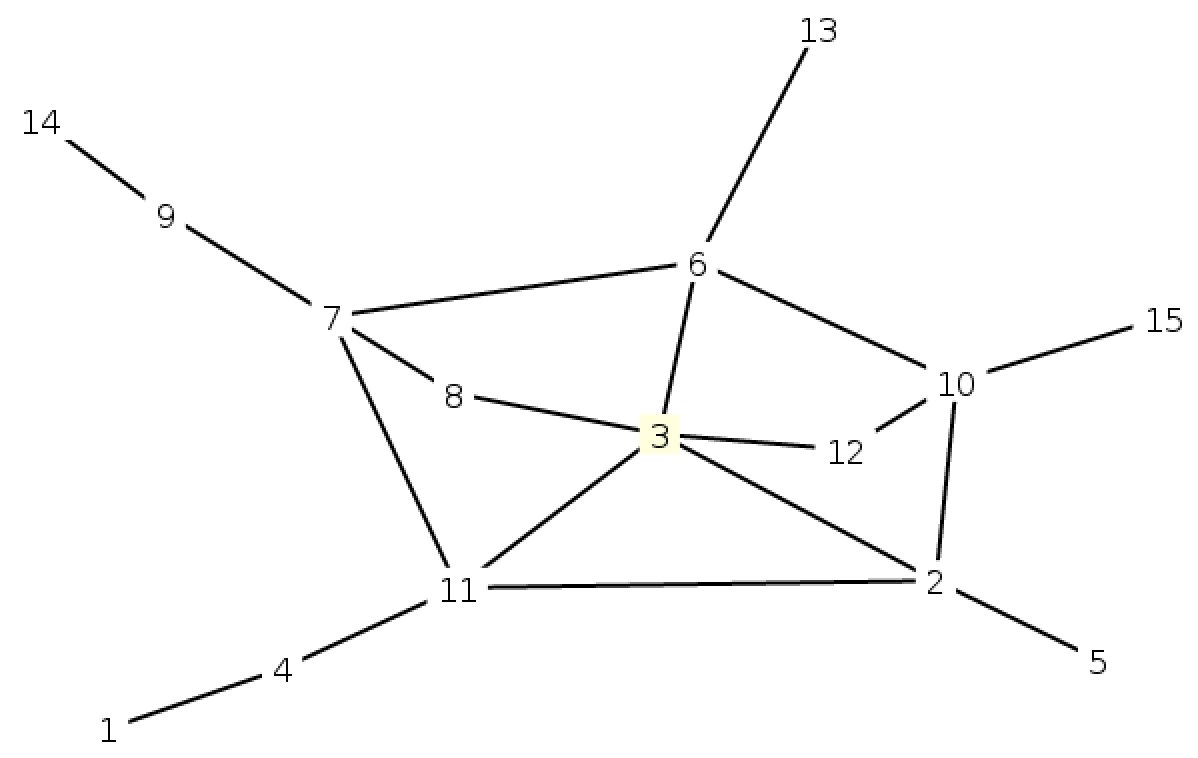
Поскольку компания Alpep известна своими необоснованными обвинениями в нарушениях патентов, мэрия города хочет проверить правомочность заявления компании.
В первой строке заданы два числа N и M ( 1 ≤ N , M ≤ 300 ) — количество станций метро и перегонов между ними. Следующие M строк содержат описания перегонов: каждая из них содержит по два числа — номера станций, между которыми есть перегон. По каждому перегону составы могут ездить как в одну, так и в другую сторону. Между любыми двумя станциями существует не более одного перегона.
Выведите « YES », если метро уездного города Н нарушает патент jMetro, и « NO » в противном случае.
Первый пример соответствует рисунку из условия.
15 19 1 4 4 11 2 10 3 2 8 7 7 6 12 10 15 10 11 2 14 9 6 13 7 9 7 11 2 5 8 3 6 10 3 6 11 3 12 3
YES
4 3 2 1 2 3 2 4
NO