Однажды в далекой-далекой стране правительство создало Министерство по сокращению бумажной волокиты. Как вы наверное догадались, это было крупнейшее министерство за всю историю страны. Количество сотрудников было поистине огромным. Несмотря на это, структура министерства была очень простой: каждый сотрудник имел не более трёх подчинённых, каждый из которых снова имел не более трех подчиненных и так далее...
В результате последних выборов был избран новый министр. Он был молод, умён и непорочен, и сразу же решил оправдать название своего учреждения. Он заметил, что многие части иерархической структуры совпадают, и решил, что должны совпадать и их обязанности. А если две структуры делают одно и тоже, одна из них является лишней, и ее работники должны быть уволены. Ваша задача найти количество различных департаментов и вывести результат в необходимом формате.
Вам дана структура министерства. Каждый работник имеет одного начальника и не более трёх подчинённых(возможно ноль). Единственным исключением является министр — у него нет начальника(но так же не более трех подчинённых). Конечно нет определённого порядка, в котором перечисляются подчинённые. Департамент состоит из должностного лица, всех его подчинённых и их подчинённых, и т.д.
Есть два особых случая:
-
Департамент, в котором должностное лицо — сам министр, тогда этот департамент есть всё министерство.
- Департамент, в котором у должностного лица нет ни одного подчинённого.
Высотой департамента назовем длину максимальной последовательность сотрудников x 1 , ..., x d такую, что сотрудник x i является начальником сотрудника x i + 1 для всех 1 ≤ i < d . Заметим что высота департамента, состоящего из одного сотрудника равна 1 .
Два департамента A и B совпадают, если существует взаимно-однозначное отображение, сопоставляющее каждому сотруднику x A из департамента A сотрудника x B из департамента B , таким образом, что сотрудник x A является начальником сотрудником y A , тогда и только тогда, когда x B является начальником y B . Заметим, что если два департамента совпадают, то они имеют одинаковую высоту, одинаковое количество сотрудников и начальнику первого департамента соответствует начальник второго.
На приведенных картинках департаменты A и B совпадают, а C не совпадает ни с A , ни c B .
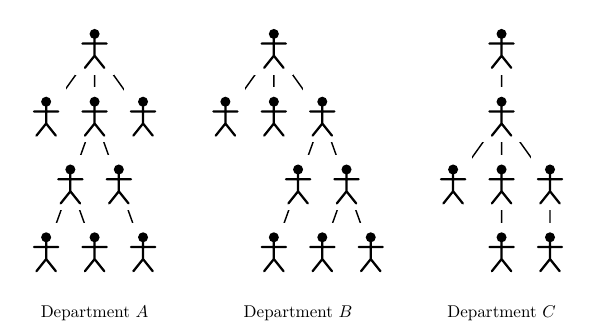
Вам необходимо для каждой высоты вычислить количество различных департаментов имеющих такую глубину. Формально требуется построить последовательность n 1 , ..., n d , где d это высота всего министерства, а n i — количество различных департаментов высоты i .
Входной файл содержит единственную строку, которая описывает иерархическую структуру министерства, используя следующую нотацию. Каждый департамент кодируются строкой "( x 1 ... x k )", где k — количество подчинённых у начальника департамента, а строки x i — коды им подчиняющихся департаментов. Департамент, состоящий из одного человека, кодируется строкой "()". Структура министерства задается кодом всего министерства. Количество сотрудников министерства не превосходит 1 000 000 (включая министра).
Выходной файл должен содержать d строк, где d это высота министерства. i -ая строка должна содержать количество различных департаментов высоты i .
Приведенная картинка иллюстрирует пример из условия.
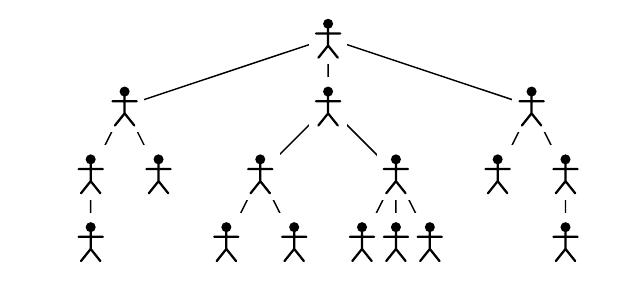
(((())())((()())(()()()))(()(())))
1 3 2 1
Глобальное потепление — это важная проблема, и Джонни знает об этом. Он решил проанализировать историю температур и найти подпоследовательной дней (не обязательно последовательных), в которой температура строго возрастает. Это убедит неверующих!
Джонни нашёл исторические данные за \(n\) последовательных дней. Температура в \(i\)-й день была \(t_i\).
Формально, нам интересно найти длину наибольшей возрастающей подпоследовательности (НВП) последовательности \((t_1, t_2, \ldots, t_n)\), то есть наибольшее такое \(k\), что возможно выбрать возрастающую последовательность индексов \(1 \leq a_1 lt a_2 \lt \ldots \lt a_k \leq n\), для которой \(t_{a_1} \lt t_{a_2} \lt \ldots \lt t_{a_k}\).
Джонни хочет найти действительно длинную подпоследовательность, а поэтому он решил сжульничать. Сначала он выберет непустой отрезок дней и целое число \(d\) (\(-x \leq d \leq x\)), а затем увеличит температуру в каждый из этих дней на \(d\). Такое небольшое изменение, вероятно, не будет обнаружено обществом, но при этом оно может сделать длину НВП больше. Разрешено выбирать \(d = 0\).
Какая максимально возможная длина НВП после такого изменения?
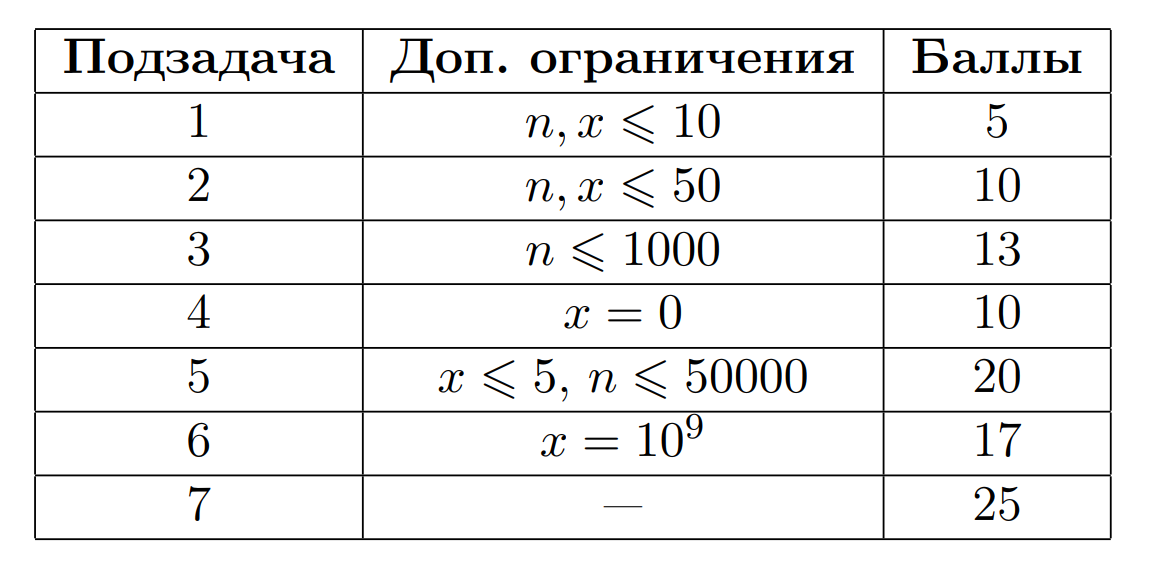
Первая строка содержит два целых числа \(n\) и \(x\) (\(1 \leq n \leq 2 \cdot 10 ^ 5\), \(0 \leq x \leq 10 ^ 9\)) — количество дней и ограничение на модуль числа \(d\).
Вторая строка содержит \(n\) целых чисел \(t_1, t_2, \ldots, t_n\) (\(1 \leq t_i \leq 10 ^ 9\)) — последовательность исторических температур.
Выведите одно целое число — максимально возможную длину НВП после одного изменения.
В примере из условия Джонни может выбрать отрезок \([2; 3]\) и \(d = -5\), что означает уменьшение \(t_2\) и \(t_3\) на 5. Тогда новая последовательность — это \((7, -2, 0, 12, 2, 7, 3, 4)\), в которой можно найти НВП \((-2, 0, 2, 3, 4)\) длины \(5\).
8 10 7 3 5 12 2 7 3 4
5
Обратите внимание на нестандартное ограничение по памяти.
Уже долгое время вы — фанат Байтлото. Примерно столько же времени ваши родственники говорят вам, что все такие игры — это пустая трата денег. Вы уверены, что это так из-за их неумения играть! У вас есть идеальный план, и скоро все увидят, как вы выигрываете.
Есть много типов игр. Вы интересуетесь в одном из них: Битлото. Выбор был прост, так как это самый простой из предлагаемых типов игр: каждый день случайно выпадает ровно одно число. Вы записываете эти числа за \(n\) последовательных дней и получаете последовательность \(a_1, a_2, \ldots, a_n\). Вы уверены, что в этой последовательности есть какая-то закономерность, а именно, в отрезках из \(l\) последовательных дней. Ваша семья всё ещё не верит вам, так что единственный способ убедить их — это использовать серьёзную математику.
Есть \(n - l + 1\) отрезок дней длины \(l\). \(i\)-й отрезок начинается в позиции \(i\) и содержит элементы \(a_i, a_{i + 1}, \ldots, a_{i + l - 1}\). Расстояние между двумя отрезками — это количество несовпадающих элементов на соответствующих позициях. Другими словами, для отрезков \(x\) и \(y\) это количество таких \(i\) (\(0 \leq i < l\)), что \(a_{x + i}\) и \(a_{y + i}\) различны. И наконец, будем говорить, что два отрезка \(k\)-похожи, если расстояние между ними не превосходит \(k\).
Зафиксированы последовательность и число \(l\). Вам даны \(q\) запросов. В каждом запросе вам дано число \(k_j\) и для каждого из \(n - l + 1\) отрезов вы должны найти количество отрезков той же длины, которые \(k\)-похожи на данный (не считая сам этот отрезок).
Первая строка содержит два целых числа \(n\) и \(l\) (\(1 \leq l \leq n \leq 10000\)) — количество дней и длину анализируемых отрезков.
Вторая строка содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(1 \leq a_i \leq 10 ^ 9\)), где \(a_i\)— число, выпавшее в \(i\)-й день.
Третья строка содержит целое число \(q\) (\(1 \leq q \leq 100\)) — количество запросов.
Каждая из следующих \(q\) строк содержит целое число \(k_j\) (\(0 \leq k_j \leq l\)) — параметр похожести для \(j\)-го запроса.
Выведите \(q\) строк. \(j\)-я строка должна содержать \(n - l + 1\) целых чисел, являющихся ответами на \(j\)-й запрос. \(i\)-е число в строке должно являться количеством других отрезков, которые \(k_j\)-похожи на \(i\)-й отрезок.

Пояснение к примеру из условия: в примере есть пять отрезков длины \(2\):
- первый содержит числа \(1\) \(2\)
- второй содержит числа \(2\) \(1\)
- третий содержит числа \(1\) \(3\)
- четвёртый содержит числа \(3\) \(2\)
- пятый содержит числа \(2\) \(1\)
Есть два запроса.
В первом запросе \(k=1\). Первый и ттретий отрезки отличаются только во второй позиции, поэтому расстояние между ними равно \(1\). Первый и четвёртый отрезки отличаются только в первой позиции, поэтому расстояние между ними равно \(1\). Это единственные два отрезка, которые \(1\)-похожи на первый отрезок, поэтому первое выведенное число равно \(2\).
Во втором запросе \(k=2\). Все пары отрезков \(2\)-похожи.
6 2 1 2 1 3 2 1 2 1 2
2 1 1 1 1 4 4 4 4 4
Джонни основывает Bytecomp — компанию, которая предлагает вычислительные мощности в облаке. Компании этого профиля обычно обладают большим количеством быстрых компьютеров, на которых производятся вычислениях их клиентов.
Джонни ещё не купил ни одного компьютера. Он пошёл в компьютерный магазин и получил список из \(n\) доступных компьютеров. Каждый компьютер характеризуется колиеством процессорных ядер \(c_i\), частотой \(f_i\) и ценой \(v_i\). Такой компьютер имеет \(c_i\) независимых ядер, не мешающих друг другу, поэтому они могут быть назначены для выполнения разных задач.
Когда клиент делает заказ на ресурс, он определяет требуемое количество ядер \(C_j\) и минимальную необходимую частоту \(F_j\). Также заказ содержит цену \(V_j\), которую клиент собирается заплатить. Если заказ принимается, Bytecomp должна предоставить эксклюзивный доступ к вычислительным мощностям, требуемым клиентом. Джонни должен выбрать \(C_j\) ядер (возможно, из разных компьютеров), каждое частотой хотя бы \(F_j\). Эти ядра не могут быть назначены какому-нибудь другому заказу.
Помогите Джонни заработать так много денег, как это возможно: выберите оптимальное подмножество заказов для исполнения, а также подмножество компьютеров из магазина, чтобы удовлетворить все принятые заказы. Ваша цель — максимизировать итоговую прибыль, то есть разность между доходом от предоставления вычислительных ресурсов клиентам и стоимостью покупки компьютеров.
Первая строка содержит целое число \(n\) (\(1 \leq n \leq 2000\)) — количество компьютеров, доступных в магазине.
Каждая из следующих \(n\) строк содержит описание одного компьютера. Она содержит три целых числа \(c_i\), \(f_i\) и \(v_i\) (\(1 \leq c_i \leq 50\), \(1 \leq f_i \leq 10^9\), \(1 \leq v_i \leq 10 ^ 9\)) — количество ядер, частота и цена, соответственно.
Следующая строка содержит целое число \(m\) (\(1 \leq m \leq 2000\)) — количество заказов.
Каждая из следующих \(m\) строк содержит описание одного заказа. Она содержит три целых числа \(C_j\), \(F_j\) и \(V_j\) (\(1 \leq C_j \leq 50\), \(1 \leq F_j \leq 10^9\), \(1 \leq V_j \leq 10^9\)) — количество запрашиваемых ядер, минимальная разрешённая частота и бюджет клиента, соответственно.
Выведите единственное целое число — максимально возможную итоговую прибыль.

Пояснение к примеру из условия: есть четыре доступных типа компьютера и три заказа. Оптимально купить четырехъядерные компьютеры стоимостью \(700\) и \(750\) (\(1450\) в сумме) и затем принять первые два заказа, получив \(300 + 1500 = 1800\). Тогда у нас есть четыре ядра с частотой \(2000\) и четыре ядра с частотой \(2200\). Мы можем назначить любые шесть из них второму клиенту (требуемая частота \(1900\)) и одно — второму клиенту (требуемая частота \(1500\)). Одно ядро не будет использоваться, что разрешено.
Итоговая прибыль равна \(1800 - 1450 = 350\).
4 4 2200 700 2 1800 10 20 2550 9999 4 2000 750 3 1 1500 300 6 1900 1500 3 2400 4550
350