Юный Мирко - умный, но озорной мальчик, который часто бродит по паркам в поисках новых идей и друзей. В этот раз он встретился с пенсионерами, которые играли в карточную игру Белот. Они пригласили его помочь им подсчитать количество очков, выигранных в одной игре.
Каждая карта определяется мастью и символом. Набор из 4 карт называется рукой. В каждой игре одна из масть "бьет" все остальные и называется козырной. Количество очков в одной игре равно сумме победных очков всех карт из всех выигравших рук в игре. Мирко заметил, что пенсионерами было выиграно N рук, а козырная масть в игре была B .
Выигрышные очки карт (если масть козырная / если масть не козырная):
А : 11 / 11
K : 4 / 4
Q : 3 / 3
J : 20 / 2
T : 10 / 10
9 : 14 / 0
8 : 0 / 0
7 : 0 / 0
По данным выигравшим рукам и козырной масти определите количество очков, выигранных в этой игре.
Первая строка содержит одно целое число N ( 1 ≤ N ≤ 100 ) и один символ B ( S , H , D или C ) - козырная масть в игре.
Каждая из следующих 4 N строк содержит описание карты K i , состоящее из двух символов: первый - символ карты ( A , K , Q , J , T , 9 , 8 , 7 ), второй - масть карты ( S , H , D или C ).
Выведите одно целое число - количество выигранных очков.
2 S TH 9C KS QS JS TD AD JH
60
4 H AH KH QH JH TH 9H 8H 7H AS KS QS JS TS 9S 8S 7S
92
Мислав любит бывать на природе, особенно в лесу. Мислав решил провести день в лесу и, так как он очень практичен, он решил не брать еду с собой. Мислав следит за фигурой, поэтому он собирается съесть не более C килограмм еды.
У него есть возможность есть грибы, которые он находит во время прогулки. Все грибы, которые ему встречаются, различны, и он собирается съесть как можно больше различных грибов, но не превысить свою норму. Мислав действует так: он идет по лесу и в любой момент может начать действовать по следующему алгоритму. Если он может съесть гриб и не переесть, то он ест его, иначе – проходит мимо.
Вам дан массив из N весов грибов в том порядке, в котором Мислав находит их. Определите, сколько грибов он может съесть.
Первая строка содержит два целых числа N и C ( 1 ≤ N ≤ 1000 , 1 ≤ C ≤ 10 6 ).
Вторая строка содержит N целых чисел w i ( 1 ≤ w i ≤ 1000 ), обозначающих веса грибов.
Выведите одно число – максимальное количество грибов, которое может съесть Мислав, чтобы не ожиреть.
В первом примере если он начнет есть с первого гриба, то он съест 3 гриба (3, 1, 1). Если он начнет со второго, то он сможет съесть 4 гриба (1, 2, 1, 1).
5 5 3 1 2 1 1
4
7 5 1 5 4 3 2 1 1
3
Юная Мирка - начинающий музыкант. Она играет на мульти-пианино. Мульти-пианино имеет бесконечно много мульти-клавиш, обозначенных целыми числами, которые можно воспринимать как ноты. Мульти-композиция (композиция для мульти-пианино) может быть представлено как последовательность чисел, обозначающих мульти-клавиши, которые должны быть нажаты (то есть ноты, которые должны быть сыграны).
Мирка услышала на мульти-радио мульти-композицию, и теперь она хочет сыграть ее. К сожалению, она не не умеет точно узнавать ноты по звуку, но может понимать, была ли нота с радио выше или ниже последней сыгранной ей ноты. Поэтому, она решила сыграть мульти-композицию следующим образом:
1. Перед началом игры, она выберет целое неотрицательное число K .
2. В начале, она сыграет правильную ноту (ее мульти-учитель сказал ей, какую клавишу нужно нажать первой)
3. Когда она услышит ноту выше, чем она только что сыграла, она будет нажимать на мульти-клавишу с числом на K больше, чем она только что сыграла.
4. Когда она услышит ноту ниже, чем она только что сыграла, она будет нажимать на мульти-клавишу с числом на K меньше, чем она только что сыграла.
5. Когда она услышит такую же ноту, как только что сыграла, она будет нажимать на ту же мульти-клавишу, что только что сыграла.
Помогите Мирке выбрать такое K , чтобы она правильно сыграла как можно больше нот мульти-композиции.
Первая строка содержит одно целое число N ( 2 ≤ N ≤ 10 6 ) - количество нот в мульти-композиции. Вторая строка содержит N целых чисел a i ( - 10 9 ≤ a i ≤ 10 9 ) - ноты мульти-композиции.
В первой строке выведите одно целое число - максимальное количество нот, которое Мирка может сыграть правильно. Во второй строке выведите одно неотрицательное целое число - значение K ( 0 ≤ K ≤ 10 9 ), которое должна выбрать Мирка, чтобы сыграть правильно максимальное количество нот. Если существует несколько решений, выведите любое.
5 1 2 0 3 1
3 2
7 2 1 -6 -2 1 6 10
5 4
Мирко и Славко играют в игру. Мирко ходит первым и выбирает непустое множество пар чисел от 1 до N (включительно). При этом числа в одной паре должны быть различны и взаимнопросты. Например, для N = 5 , Мирко может выбрать такое множество пар: {(1, 2), (3, 4), (2, 5), (3, 5)}.
Славко ходит вторым и его задача - найти разделяющий элемент для множества пар Мирко. Разделяющим элементом для множества пар называется такое число x из диапазона [2: N ] , что для каждой пары ( a , b ) из множества выполняется одно из двух условий:
1. a , b < x
2. a , b ≥ x
Например, множество пар {(1, 2), (3, 4)} имеет разделяющий элемент x = 3 .
Если разделяющий элемент существует, Славко обязательно его найдет, и тогда он выиграет. Мирко же выиграет, если Славко не сможет найти разделяющий элемент. Он просит вас помочь: определите, как много множеств пар, удовлетворяющих условию, он может выбрать, чтобы гарантированно выиграть. Так как это число может быть очень большим, выведите его по модулю 1 000 000 000.
Единственная строка содержит одно целое число N ( 1 ≤ N ≤ 20 ).
Выведите одно целое число - ответ на вопрос Мирко по модулю 1000000000.
2
1
3
5
4
21
Одаренный предпринимательским талантом Мистер Картошечка открывает два новых магазина, где, как вы, вероятно, уже догадались, он будет продавать картошечку. Мистер Картошечка получает картошку от N фермеров. Каждый фермер предлагает ровно a i картофелин с мешке общей стоимостью c i . Мистер Картошечка собирается купить по мешку картошки у кадого из фермеров и распределить их в два своих магазина.
Обозначим среднюю цену картошки в магазинах за P 1 и P 2 . Средняя цена равняется отношению суммарной стоимости к количеству картошки в данном магазине. Мистер Картошечка хочет, чтобы значение P 1 · P 2 было минимальным.
Кроме того, хотя бы в одном магазине дожно быть ровно L мешков картошки.
В первой строке содержатся два целых числа N и L ( 1 ≤ L < N ≤ 100 ).
Вторая строка содержит N целых чисел a i ( 1 ≤ a i ≤ 100 ), разделенных пробелами.
Третья строка содержит N целых чисел c i ( 1 ≤ c i ≤ 10 6 ), разделенных пробелами.
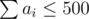 .
.
Выведите одно вещественное число, округлённое до 3 знаков после запятой – минимальное возможное значение P 1 · P 2 .
30 баллов: N ≤ 20 .
3 1 3 2 1 1 2 3
0.556
3 2 2 2 2 3 3 3
2.250