В далекой стране есть N городов. Был избран новый премьер-министр. В настоящее время в этой стране нет ни одной дороги, поэтому премьер-министр решил модернизировать страну, соединив некоторые города с двусторонними автострадами в транспортные сети. Два города будут расположены в одной и той же сети, если можно добраться до одного города от другого, используя недавно построенные дороги. Каждый город будет расположен в какой-то сети. Каждая сеть состоит из одного или нескольких городов.

Города представлены в виде точек в двумерной системе координат. Дорога между двумя городами представлена ​​в виде отрезка, соединяющего две точки, в которых расположены города. Длина дороги равна длине отрезка в километрах.

В настоящее время страна переживает экономический спад, поэтому премьер-министр решил, что из-за отсутствия бюджета они не будут строить дороги длиннее, чем D километров. Кроме того, премьер-министр радуется мелочам, поэтому он будет счастлив, если по крайней мере в одной сети будет существовать непустое подмножество городов (оно может включать все города в сети), где общая сумма жителей делится на К . Например, если K = 4 и есть сеть с городами, в которых есть 3 , 5 , 7 жителей соответственно, премьер-министр будет счастлив, потому что сумма жителей в первых двух городах равна 8 .

Помогите премьер-министру сократить расходы, определив минимальный уровень D , необходимый для того чтобы премьер-министр мог строить дороги и одновременно быть счастливым.

Марко обнаружил новую функцию на его телефоне - Т9. На его телефоне имеется стандартная клавиатура на 9 кнопок:

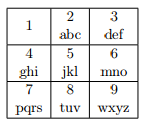
Для того чтобы вводить текст на этой клавиатуре необходимо несколько раз нажимать клавишу с соответствующей буквой. Точнее, если это первая буква на клавише, нужно нажать 1 раз, если вторая буква - 2 раза, и так далее. Например, если мы хотим ввести слово "giht", то необходимо нажать клавиши следующим образом: g-4 i-444 h-44 t-8. Новая возможность, которую открыл Марко, упрощает ввод текста, потому что больше не требуется нажимать по одной клавише несколько раз подряд - достаточно всего одного нажатия. Программа будет пытаться понять, какое слово из словаря вы пытаетесь ввести.

Марко довольно скептически относится к новым технологиями (как минимум к новым для него) и он боится, что ошибки будут довольно часто. Марко наизусть знает весь словарь мобильного телефона. Он состоит из N слов, состоящих из строчных латинских букв, длина каждого слова не превышает 1000000 символов. Марко даст массив нажатий на клавиши S длиной не более 1000, и хочет узнать как много слов из словаря он может получить при такой последовательности нажатий если используется функция Т9.

Учитель отправил своим ученикам письмо со следующим заданием: "Напишите программу, которая определит значение X по следующему выражению: X = number ₁ ^{pot ₁} + number ₂ ^{pot ₂} + ... + number _n ^{pot _n} если известно, что number ₁ , number ₂ , ... , number _n - натуральные числа, а pot ₁ , pot ₂ , ... , pot _n - однозначные натуральные числа."

К сожалению, из-за того что учитель был очень глупый, при записи формулы на компьютер, форматирование текста было потеряно и формула для значения X превратилось в сумму N чисел: X = P ₁ + P ₂ + ... + P _n . Например, без форматирования изначальная формула X =  21 ² + 123 ⁵ превратилась в формулу X =  212 + 1235 . Помогите глупому учителю написать программу, которая по новой формуле (то есть по данным числам P ₁ , P ₂ , ... , P _n ) восстановит изначальное значение X .

Абсолютное зло, называемое выпускным экзаменом, приближается к ученикам старших классов этого года. Одним из заданий должно быть написание эссе на их родном языке. Мирко предчувствует, что правящая партия "Единая Хорватия" выполнит свои предвыборные обещания касательно компьютеризации в государственных учреждениях, поэтому он полагает, что эссе в этом году будут проверяться не человеком, а новейшими японскими супер-компьютерами "Кудахтер-3000". Мирко имеет большие опасения по этому поводу, и хочет написать эссе так, чтобы оно прошло основные критерии проверки. Благодаря тому, что его отец работает в министерстве образования, он их узнать. Эссе пройдет проверку, если:

1. Оно содержит не менее чем A и не более чем B слов.

2. Каждое слово содержит не менее 1 и не более 15 символов.

3. Используемый словарный запас достаточно велик, иными словами, эссе содержит хотя бы 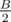различных слов.

Мирко сейчас очень занят, готовясь к экзаменам, поэтмоу он просит вас помочь ему в написании эссе. Оно должно быть выведено в одну строчку, состоять только из строчных латинских букв и пробелов.

Ученые в тайной химической лаборатории в Хорватии изучают химические связи в недавно обнаруженном веществе инопланетного происхождения. Имеющаяся в распоряжении ученых порция вещества состоит из N молекул, соединенных между собой N - 1 ковалентными связями, и все молекулы объединены этими связями (не обязательно напрямую) в единую сеть.

Так как вещество нестабильное, в каждой молекуле регулярно возникают импульсы, перемещающиеся по веществу через существующие связи в обоих направлениях. Ученые собираются стабилизировать вещество, направив ковалентные связи (то есть, дав импульсам возможность путешествовать по ним между молекулами лишь в одном направлении). Показатель нестабильности вещества определяется длиной максимального пути, который может пройти импульс в нем, и ученые хотят сделать эту величину как можно меньше.

Помогите ученым создать вещество с минимальным показателем нестабильности, указав необходимое направление ковалентных связей.