Учитель отправил своим ученикам письмо со следующим заданием: "Напишите программу, которая определит значение X по следующему выражению: X = number 1 pot 1 + number 2 pot 2 + ... + number n pot n если известно, что number 1 , number 2 , ... , number n - натуральные числа, а pot 1 , pot 2 , ... , pot n - однозначные натуральные числа."
К сожалению, из-за того что учитель был очень глупый, при записи формулы на компьютер, форматирование текста было потеряно и формула для значения X превратилось в сумму N чисел: X = P 1 + P 2 + ... + P n . Например, без форматирования изначальная формула X = 21 2 + 123 5 превратилась в формулу X = 212 + 1235 . Помогите глупому учителю написать программу, которая по новой формуле (то есть по данным числам P 1 , P 2 , ... , P n ) восстановит изначальное значение X .
Первая строка содержит одно целое число N ( 1 ≤ N ≤ 10 ), количество чисел в формуле. Каждая из следующих N строк содержит одно целое число P i ( 10 ≤ P i ≤ 9999 ) - соответствующий элемент формулы.
Выведите единственное целое число - изначальное значение X .
2 212 1253
1953566
5 23 17 43 52 22
102
3 213 102 45
10385
Абсолютное зло, называемое выпускным экзаменом, приближается к ученикам старших классов этого года. Одним из заданий должно быть написание эссе на их родном языке. Мирко предчувствует, что правящая партия "Единая Хорватия" выполнит свои предвыборные обещания касательно компьютеризации в государственных учреждениях, поэтому он полагает, что эссе в этом году будут проверяться не человеком, а новейшими японскими супер-компьютерами "Кудахтер-3000". Мирко имеет большие опасения по этому поводу, и хочет написать эссе так, чтобы оно прошло основные критерии проверки. Благодаря тому, что его отец работает в министерстве образования, он их узнать. Эссе пройдет проверку, если:
1. Оно содержит не менее чем A и не более чем B слов.
2. Каждое слово содержит не менее 1 и не более 15 символов.
3. Используемый словарный запас достаточно велик, иными словами, эссе содержит хотя бы
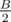 различных слов.
различных слов.
Мирко сейчас очень занят, готовясь к экзаменам, поэтмоу он просит вас помочь ему в написании эссе. Оно должно быть выведено в одну строчку, состоять только из строчных латинских букв и пробелов.
В единственной строке содержатся два целых числа - A и B ( 1 ≤ A ≤ B ≤ 100000 ).
В единственной строке выведите эссе, удовлетворяющее условию задачи при данных A и B .
2 7
b c d e f g h
26 30
b c d e f g h i j ab bb cb db eb fb gb hb ib jb ac bc cc dc ec fc gc hc ic jc ad
19 19
b c d e f g h i j ab bb cb db eb fb gb hb ib jb
Ученые в тайной химической лаборатории в Хорватии изучают химические связи в недавно обнаруженном веществе инопланетного происхождения. Имеющаяся в распоряжении ученых порция вещества состоит из N молекул, соединенных между собой N - 1 ковалентными связями, и все молекулы объединены этими связями (не обязательно напрямую) в единую сеть.
Так как вещество нестабильное, в каждой молекуле регулярно возникают импульсы, перемещающиеся по веществу через существующие связи в обоих направлениях. Ученые собираются стабилизировать вещество, направив ковалентные связи (то есть, дав импульсам возможность путешествовать по ним между молекулами лишь в одном направлении). Показатель нестабильности вещества определяется длиной максимального пути, который может пройти импульс в нем, и ученые хотят сделать эту величину как можно меньше.
Помогите ученым создать вещество с минимальным показателем нестабильности, указав необходимое направление ковалентных связей.
Первая строка содержит одно целое число N ( 2 ≤ N ≤ 100000 ). Каждая из последующих N - 1 строк содержит по два целых числа a i и b i ( 1 ≤ a i , b i ≤ N ), которые показывают что молекулы с номерами a i и b i соединены ковалентной связью.
Выведите N - 1 строку, каждая из которых должна содержать 1 если ковалентная связь должна быть направлена от a i к b i или 0 в противном случае.
Решения, в которых N ≤ 20 , будут оцениваться в 30 баллов.
3 1 2 2 3
0 1
4 2 1 1 3 4 1
1 0 1
Слон постоянно шалит в своей школе. На уроках ему становится скучно, и он начинает хулиганить. Учитель решил успокоить слона, поэтому дал ему очень сложную математическую задачу.
Учитаель дал слону арифметическое выражение A и числа P и M . Слону надо ответить на такой вопрос: "Каково минимальное неотрицательное значение переменной x в выражении A , такое что остаток от деления A на M равно P ?". Гарантируется, что решение всегда существует.
Кроме того, после применения законов распределения к выражению A , x содержится в A только в первой степени.
В первой строке содержится выражение A ( 1 ≤ | A | ≤ 10 5 ). Вторая строка содержит два целых числа P и M ( 0 ≤ P < M ≤ 10 6 ). A состоит только из символов +, -, *, (, ), x и цифр от 0 до 9. Каждый оператор +, -, * применяется ровно к двум значения, умножения всегда обозначены явно.
Выведите одно число – ответ на задачу
Пояснение к первому примеру:
(5 + 3 + x ) mod 10 при x = 0 равно 8.
(5 + 3 + x ) mod 10 при x = 1 равно 9. Значит, ответ x = 1 .
5+3+x 9 10
1
20+3+x 0 5
2
3*(x+(x+4)*5) 1 7
1
|
Дан массив a длины n , состоящий из натуральных чисел в диапозоне [1; k ] . Вам необходимо обработать 2 типа запросов:
1 p u — изменить значение элемента на позиции p на u .
2 — сообщить длину кратчайшего подотрезка, содержащего все числа от 1 до k или - 1 если такого подотрезка не существует.
В первой строке входного файла задано 3 целых числа n , k и m (1 ≤ n , m ≤ 10 5 , 1 ≤ k ≤ 50) — длина массива, максимальное число в массиве и число запросов, соответственно.
В следующей строке содержится n чисел (1 ≤ a i ≤ k ) — элементы массива.
В последующих m строках содержатся запросы в формате, указанном выше.
Для каждого запроса второго типа выведите ответ на него.
11 баллов — (1 ≤ n , m ≤ 40) .
47 балла — (1 ≤ n , m ≤ 5 000) .
42 балла — (1 ≤ n , m ≤ 10 5 ) потестовая оценка.
4 3 5 2 3 1 2 2 1 3 3 2 1 1 1 2
3 -1 4