Каждый год в одном из уголков нашей вселенной проходят Интеллектуальные Олимпийские Игры. В этом году честь проводить это масштабное мероприятие выпала планете Юпитер. Вам предстоит отобрать две команды на Игры из имеющихся n кандидатов в сборную.
Все кандидаты являются школьниками, каждый кандидат учится в определенном классе. Как и на Земле, на Юпитере 11 классов, пронумерованных от 1 до 11. На Игры отбирается две команды по результатам отборочных соревнований. На соревнованиях проводится пять отборочных туров. По итогам каждого тура каждый школьник может набрать от 0 до 300 баллов, чем больше, тем лучше.
В первую команду попадают четыре лучших школьника по сумме баллов, набранных на всех отборочных турах. Во вторую команду попадают четверо лучших по сумме баллов из тех, кто не попал в первую команду, и при этом не учится в 11 классе.
Все туры уже проведены, и получилось так, что любые два кандидата набрали в сумме различное количество баллов. Осталось лишь написать программу, которая по имеющимся данным о кандидатах и результатах туров определит тех восьмерых, которые защитят честь Юпитера на Интеллектуальных Олимпийских Играх и докажут, что Юпитер — суперпланета!
Первая строка входных данных содержит единственное число n — количество кандидатов в сборную Юпитера ( 8 ≤ n ≤ 500 ).
Следующие n строк содержат информацию о кандидатах. Каждая строка содержит 6 целых чисел — номер класса, в котором учится очередной кандидат, и его результаты на отборочных турах.
Номер класса является числом от 1 до 11, а результат на каждом туре — числом от 0 до 300.
Гарантируется, что все участники имеют различные суммарные баллы.
Гарантируется, что есть хотя бы 8 кандидатов, обучающихся не в 11 классе.
Выведите две строки.
Первая строка должна содержать четыре целых числа, разделенных пробелами — номера кандидатов, которые попадут в первую команду Юпитера. Кандидаты нумеруются с единицы в порядке их появления во вводе. Выводить номера следует в порядке возрастания.
Вторая строка должна описывать вторую команду Юпитера в аналогичном формате.
10 9 50 271 287 282 42 10 230 241 137 14 240 10 276 109 300 197 300 8 205 292 194 232 74 10 294 291 299 300 255 9 195 275 265 134 9 11 204 259 96 263 83 7 141 223 85 84 26 11 286 294 289 221 261 10 277 52 117 272 262
3 4 5 9 1 2 6 10
Маше на день рождения подарили набор матрёшек!
Теперь Маша сидит и вкладывает их одна в другую. Она заметила, что матрёшки отличаются по размеру, и одна помещается внутри другой, только если ее размеры строго меньше. Так, если есть две матрёшки i и j , а их размеры a i и a j соответственно, то матрёшка i вкладывается внутрь матрёшки j тогда и только тогда, когда a i < a j . Разумеется, непосредственно внутрь матрёшки можно вложить только одну другую матрёшку, иначе получится неаккуратно, а Маша — очень аккуратная девочка.
Маше особенно нравится, если она может, вкладывая матрёшки друг в друга, добиться того, что все они оказываются внутри одной самой большой матрёшки. Но, к сожалению, это не всегда возможно. Поэтому Маша решила убрать часть матрёшек в шкаф, оставив такой набор, чтобы их все можно было вложить друг в друга. Помогите Маше понять, какое максимальное количество матрёшек может быть в таком наборе.
В первой строке находится число n — количество матрёшек, подаренных Маше ( 1 ≤ n ≤ 1000 ). В следующей строке через пробел находятся n чисел — размеры матрёшек. Число a i , стоящее на месте i , задает размер матрёшки с номером i ( 1 ≤ a i ≤ 10 000 ).
Выведите одно число — максимальное количество матрёшек, которые можно вложить друг в друга.
3 2 10 2
2
6 2 1 2 1 3 4
4
4 3 1 4 2
4
Условие пока не опубликовано...
4 4 /\/\ \../ .\.\ ..\/
8
На Марсе есть большой полигон для испытания роботов. Он представляет собой таблицу из n строк и m столбцов, столбцы которой направлены с севера на юг, а строки — с запада на восток. В каждой клетке таблицы находится ускоритель, направленный в одну из сторон света.
Находясь в клетке, робот может воспользоваться ускорителем в ней. При этом он попадает в соседнюю с текущей клетку в направлении ускорителя и не тратит топливо. Если соседней клетки в направлении ускорителя нет, то им нельзя воспользоваться. Также робот может не пользоваться ускорителем и переместиться в любую из соседних клеток, затратив один литр топлива.
Сегодня роботу дали следующее задание: ему надо доехать из первой клетки первого столбца в последнюю клетку последнего столбца. Напишите программу, которая определит, какое минимальное количество топлива ему придется для этого потратить.
Рисунок ниже показывает полигон, заданный в примере. Ускорители показаны в виде стрелок. Заштрихованы клетки, по которым оптимально проехать роботу. Ускорители, которыми робот воспользовался, показаны жирными стрелками.
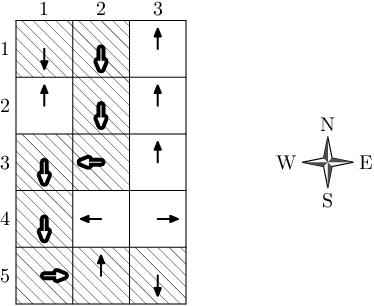
Первая строка входных данных содержит два числа n и m — протяженность полигона с севера на юг и с запада на восток ( 1 ≤ n , m ≤ 20 ).
Следующие n строк содержат по m латинских букв, описывающих направления ускорителей в очередной строке. Буква соответствуют направлению ускорителя: N — на север, W — на запад, S — на юг, E — на восток. Строки занумерованы с севера на юг, а столбцы с запада на восток. Таким образом, направление на север соответствует уменьшению номера строки, направление на юг — увеличению номера строки, направление на запад — уменьшению номера столбца, а направление на восток — увеличению номера столбца.
Выведите одно целое число — минимальное количество литров топлива, которое должен потратить робот, чтобы выполнить задание.
5 3 SSN NSN SWN SWE ENS
2
Петя очень любит компьютерные игры. Недавно он обнаружил в интернете интересную ролевую игру. Управляя героем, надо искать магические артефакты и получать золото.
К сожалению, первый же квест в игре поставил Петю в тупик. Выполнив задание, он получил n магических артефактов, которые можно использовать для получения золота. Для каждого артефакта известна его ценность , для i -го артефакта она равна w i . Для получения золота артефакты можно активировать . Каждый артефакт можно активировать только один раз. Петя может активировать артефакты в произвольном порядке.
У героя, которым управляет Петя, есть магическая сила , исходно она равна нулю. Есть два способа активировать артефакт: с помощью магии и с помощью силы. Если активировать артефакт с ценностью w с помощью магии, то магическая сила героя увеличивается на w . Если же активировать артефакт с ценностью w с помощью силы, то герой получает xw золотых монет, где x — магическая сила героя в момент активации артефакта.
Например, если герой Пети получил 4 артефакта с ценностями 1, 1, 2 и 2, то можно получить 9 золотых монет, действуя следующим образом. Сначала надо активировать с помощью магии по одному артефакту с ценностью 1 и 2. После этого магическая сила героя равна 3, теперь можно активировать с помощью силы оставшиеся артефакты и получить 3 и 6 золотых монет, соответственно.
Помогите Пете определить, какое максимальное количество золотых монет он может получить, активировав артефакты в правильном порядке оптимальным образом.
Первая строка входных данных содержит единственное число n — количество магических артефактов ( 1 ≤ n ≤ 100 ).
Вторая строка входных данных содержит n чисел w 1 , w 2 , ..., w n — ценности артефактов ( 1 ≤ w i ≤ 100 ).
Выведите максимальное возможное число золотых монет, которые можно получить с помощью магических артефактов.
4 1 1 2 2
9