В этой задаче Вам вновь придется помочь Берляндии. Эта страна состоит из \(n\) городов, некоторые пары из которых соединены двусторонними дорогами, каждая дорога характеризуется своей длиной. Все города пронумерованы числами от 1 до \(n\), столица имеет номер 1. Время от време ни Президент объезжает страну, посещая города страны. Целью каждой поездки является один из городов, к которому он едет из столицы вдоль дорог одним из кратчайших путей.
В далекие времена (когда задачи на алгоритм Дейкстры вызывали сложность) специальное ведомство составила такой набор дорог \(T\), вдоль которого можно было проехать из столицы в любой город, причем единственным образом. Разумеется, путь по дорогам из набора \(T\) из столицы в каждый город являлся кратчайшим. Особо умные жители страны попросту называли этот набор дорог "деревом кратчайших путей". Известно, что Президент пользовался дорогами из \(T\) во время своих поездок. За прошедшие годы этот набор перестал быть секретным, и, поэтому, стал объектом повышенного внимания берляндских экстремистов. У специального ведомства новое задание. Для каждого города кроме столицы необходимо вычислить кратчайшее расстояние до него, при условии, что та дорога по которой Президент должен был закончить свой путь в этот город является атакованной и проезжать по ней нельзя.
В первой строке входного файла записана пара целых чисел \(n\) и \(m\) (\(2 \leq n \leq 4\,000\); \( n - 1 \leq m \leq 100\,000\)), где \(n\) — количество городов в стране, а \(m\)— количество дорог в этой стране. Далее в \(m\) строках содержатся описания дорог, по одной дороге в строке. Каждая дорога задается четверкой целых чисел \(a_j\), \(b_j\), \(l_j\), \(t_j\) , где \(a_j\), \(b_j\) это номера городов, соединяемых дорогой (\(1 \leq a_j, b_j \leq n\); \(a_j \neq b_j\)), \(l_j\) — ее длина (\(1 \leq l_j \leq 10^5\)), а \(t_j\) равно 1 если дорога принадлежит дереву кратчайших путей и 0 в противном случае.
Гарантируется, что набор \(T\) удовлетворяет описанным выше свойствам. Между парой городов может быть более одной дороги. Все дороги двусторонние.
Выведите \(n - 1\) число в строку через пробелы. \(i\)-ое число должно быть равно либо длине кратчайшго пути из столицы в город \(i + 1\), при условии, что по той дороге из \(T\), которой Президент заканчивал свой путь в этот город, передвигаться нельзя, либо -1, если добраться до города \(i + 1\) вообще невозможно.
5 9 3 1 3 1 1 4 2 1 2 1 6 0 2 3 4 0 5 2 3 0 3 2 2 1 5 3 1 1 3 5 2 0 4 5 4 0
6 7 8 5
Постановка задачи о {Наименьшем общем предке} такова: дано дерево T с выделенным корнем и две вершины u и v, lca(u, v) - вершина с максимальной глубиной, которая является предком и u, и v. Например, в картинке внизу lca(8, 7) - вершина 3.
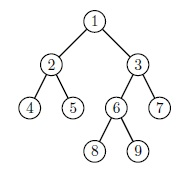
С помощью операции chroot(u) мы можем менять корень дерева, достаточно отметить u, как новый корень, и направить ребра вдоль пути от корня. Наименьшие общие предки вершин поменяются соответствующе. Например, если мы сделаем chroot(6) на картинке сверху, lca(8, 7) станет вершина 6. Получившееся дерево изображено снизу.
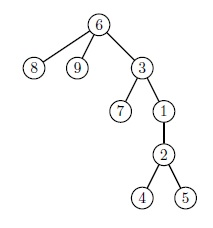
Вам дано дерево T. Изначально корень этого дерева - вершина 1. Напишите программу, которая поддерживает эти две операции: lca(u, v) и chroot(u).
Входной файл состоит из нескольких тестов.
Первая строка каждого теста содержит натуральное число n — количество вершин в дереве (1 ≤ n ≤ 100 000). Следующие n - 1 строки содержат по 2 натуральных числа и описывают ребра дерева. Далее идет строка с единственным натуральным числом m — число операций —. Следующие m строк содержат операции. Строка "? u v" означает операцию lca(u, v), a строка "! u" - chroot(u). Последняя строка содержит число 0.
Сумма n для всех тестов не превосходит 100 000. Сумма m для всех тестов не превосходит 200 000.
Для каждой операции "? u v" выведите значение lca(u, v). Числа разделяйте переводами строк.
Система тестов состоит из двух групп:
Первая группа состоит из тестов, для которых выполняется ограничение \(n \le 100\), \(m \le 10000\). За прохождение всех тестов группы ставится 55 баллов.
Вторая группа стоит из тестов, в которых нет дополнительных ограничений. За прохождение тестов этой группы и всех предыдущих тестов ставится дополнительно 45 баллов.
9 1 2 1 3 2 4 2 5 3 6 3 7 6 8 6 9 10 ? 4 5 ? 5 6 ? 8 7 ! 6 ? 8 7 ? 4 5 ? 4 7 ? 5 9 ! 2 ? 4 3 0
2 1 3 6 2 3 6 2
Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 100000) вершин, пронумерованных от 0 до n - 1. Требуется ответить на m (1 ≤ m ≤ 100000) запросов о наименьшем общем предке для пары вершин.
Запросы генерируются следующим образом. Заданы числа a1, a2 и числа x, y и z. Числа a3, ..., a2m генерируются следующим образом: ai = (x·ai - 2 + y·ai - 1 + z)mod: n. Первый запрос имеет вид (a1, a2). Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид ((a2i - 1 + v)mod: n, a2i).
Первая строка содержит два числа: n и m. Корень дерева имеет номер 0. Вторая строка содержит n - 1 целых чисел, i-е из этих чисел равно номеру родителя вершины i. Третья строка содержит число содержит два целых числа в диапазоне от 0 до n - 1: a1 и a2. Четвертая строка содержит три целых числа: x, y и z, эти числа неотрицательны и не превосходят 109.
Выведите в выходной файл сумму номеров вершин — ответов на все запросы.
3 2 0 1 2 1 1 1 0
2
Чип и Дейл спешат на помощь! Но внимательные зрители знают, что помощь как правило нужна самим Чипу и Дейлу, поэтому сегодня вам надо будет сыграть роль сообразительной Гаечки. Итак, Чип и Дейл снова попали в лапы к Толстопузу. Кот очень не любит грызунов и поэтому приготовил им изощренное испытание. Он собирается поместить их в лабиринт и посмотреть смогут ли они из него выбраться. Лабиринт представляет собой дерево, в котором каждое ребро имеет одно направление. Гаечка подслушала разговор Толстопузу со своими сообщниками и теперь знает несколько возможных вариантов: в какую точку лабиринта поместят её друзей, и где будет выход. Для каждого такого варианта она хочет понять, смогут ли Чип и Дейл найти выход, или нет.
В первой строке записано число \(n\) (\(n \leq 10^5\)) - количество вершин дерева. В следующих \(n-1\) строках описаны ребра дерева. В \(i+1\)-ой строке записано номера вершин \(a_i, b_i\), означающие, что в дереве есть ребро из вершины \(a_i\) в вершину \(b_i\).
Далее на отдельной строке записано число \(m\) (\(m \leq 10^5\)) -- количество запросов. После этого идут \(m\) строк с описанием запросов, в \(n + 1 + i\)-ой строке записаны через пробел числа \(x_i\) и \(y_i\).
Для каждого запроса на отдельной строке требуется вывести Yes, если в графе есть путь между вершинами \(x_i\) и \(y_i\), и No иначе.
| input.txt | output.txt |
4 1 2 3 1 4 1 6 1 2 3 2 2 3 4 2 4 3 2 1 | Yes Yes No Yes No No |
Гора состоит из площадок, соединенных между собой узкими проходами. На каждой площадке лежит какое-то количество камней. У разных площадок разный рейтинг, зависящий от высоты площадки — чем выше площадка, тем больше ее рейтинг среди камней. Очевидно, что на площадках с более высоким рейтингом лежит большее количество камней.
В один солнечный день главный камень одной из площадок обратил внимание, что вокруг стало очень тесно. Но камни не могут катиться вверх, а на нижние площадки они катиться не хотят из-за плохого рейтинга. Поэтому главный камень пошел на хитрость. Он выбрал M камней и сказал каждому из них, что где-то внизу появилась замечательная площадка с самым высоким рейтингом на горе. Для полной правдоподобности он составил карту площадок, на которые можно скатиться с его площадки. Всего (включая переполненную площадку) оказалось N площадок. Поскольку главный камень ленивый, он не стал рисовать все пути между площадками, а просто нарисовал минимальное количество проходов между площадками, чтобы из его площадки можно было добраться в любую, находящуюся ниже. Он показал каждому из M камней эту карту и объяснил, где находится замечательная площадка (чтобы камень запомнил путь). Причем, чтобы главные камни нижних площадок не имели к нему претензий из-за такого нашествия, некоторым камням он показал на другие площадки, чем остальным. Чтобы не создать лавину, он сказал камням катиться с небольшим интервалом между собой. Немного подумав, он решил, что можно пускать камни парами, чтобы пространство быстрее освободилось. Камни ему поверили и стали собираться в дорогу.
Камни не любят скучать, поэтому каждая пара решила посчитать, сколько времени они будут катиться вместе, и, может быть, перестроить пары, чтобы увеличить это время. На то, чтобы скатиться по проходу с одной площадки в следующую, не заходя по пути на другие площадки, камень тратит одну минуту. Но складывать числа камни не умеют, в этом им требуется ваша помощь.
В первой строке входного файла записаны два целых числа - N и K , где 1 ≤ N ≤25000, K = M / 2, 0 ≤ M ≤ 2000 . В следующих ( N –1) строках находятся пары чисел i и j , означающие, что из i -й площадки можно напрямую скатиться на j -ю. Площадки занумерованы числами от 1 до N , верхняя площадка, откуда катятся камни, может иметь любой номер. Записанных пар номеров площадок достаточно, чтобы определить путь из самой верхней площадки до любой другой. Дальше идут K строк, на каждой строке через пробел записана пара чисел a и b (1 ≤ a , b ≤ N ) , обозначающая пункты назначения для очередной пары камней: первый камень катится на площадку a , а второй — на площадку b .
В выходной файл нужно вывести K строк, на каждой строке должно находиться по три целых числа a , b и c , записанных через пробел. Эти числа означают, что пара камней, направляющихся на площадки a и b , будет катиться вместе c минут. Тройки чисел нужно выдавать в том же порядке, в котором перечислены соответствующие им пары во входном файле.
6 2 1 2 1 3 1 4 3 5 3 6 2 4 5 6
2 4 0 5 6 1