#197

Темы: [Размещения с повторениями] [Формула]

Максимальное время работы на одном тесте:

1 секунда

Пусть дана перестановка π. Обозначим φ[i] - количество таких j, что π[j] > π[i], а j < i. φ называется таблицей инверсий перестановки π. Требуется по данной таблице инверсий восстановить перестановку.

Входные данные

В первой строке входных данных содержится число 0 < N <= 2000 - количество чисел в перестановке π. Во второй строке записана таблица инверсий φ.

Выходные данные

Выведите искомую перестановку π.

Примеры

Входные данные

3
0 0 2

Выходные данные

2 3 1

#601

Забор

Темы: [Формула]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Окружная олимпиада, 2007, 2 тур, Задача A ]

Том Сойер получил важное задание по покраске забора. Забор состоит из n досок. Он когда-то был покрашен, однако с некоторых участков забора краска облупилась. Эти доски Тому и необходимо покрасить. Так как забор большой, пришлось подвезти к забору целую цистерну с краской. Цистерна была помещена у края забора и не может перемещаться. У Тома есть ведерко, набрав краски в которое, Том может покрасить $k$ досок забора. При этом Том может в любой момент вернуться за краской к цистерне.

Изначально Том находится у цистерны. Соседние доски находятся на расстоянии 1 фута друг от друга, цистерна находится на расстоянии 1 фута от первой доски. По окончании работы Том должен положить кисточку и ведерко на свою исходную позицию рядом с цистерной.

Требуется выяснить, какое минимальное расстояние Тому необходимо пройти, чтобы покрасить забор.

Входные данные

Первая строка входного файла содержит количество досок в заборе $n$ (1 ≤ $n$ ≤ $10^9$) и вместимость ведерка $k$ (1 ≤ $k$ ≤ 100). Во второй строке содержится количество неокрашенных отрезков забора $m$ (1 ≤ $m$ ≤ 50). Далее следуют $m$ строк, в каждой из которых описан один неокрашенный отрезок. Отрезок описывается своей левой границей $l_i$ и правой границей $r_i$ (1 ≤ $l_i$ ≤ $r_i$ ≤ $n$). Такое описание означает, что не покрашены $l_i$-я, ($l_i$+1)-я, …, ($r_i$–1)-я, $r_i$-я доски забора (доски нумеруются от 1 до $n$). Гарантируется, что неокрашенные отрезки, заданные во входном файле, не пересекаются.

Выходные данные

Выведите одно число — минимальное расстояние в футах, которое необходимо пройти Тому для выполнения своего ответственного задания.

Примеры

Входные данные

Выходные данные

#990

Праздники

Темы: [Перебор с отсечением] [Дата и время] [Формула]

Источники: [ Личные олимпиады, Московская олимпиада школьников, 10-11 классы, 2005, 1 день, Задача A ]

Нерабочими называются выходные, а также праздники: 23 февраля, 8 марта и K первых дней года. Праздник попавшие на выходные, переносятся. По заданному K требуется определить максимальное количество подряд идущих нерабочих дней.

Парламент некоторой страны принял новый закон о праздничных днях. Согласно этому закону первые K дней года, а также 23 февраля (День олимпиады по информатике) и 8 марта объявляются праздничными, а все остальные праздники отменяются. При этом все выходные (суббота и воскресенье), попавшие на праздничные дни, переносятся на следующие за этими праздниками рабочие дни.

В зависимости от того, на какой день недели приходится 1 января, количество нерабочих дней, которые идут подряд, может меняться.

Требуется определить, какое наибольшее количество нерабочих дней может идти подряд.

Входные данные

На вход подается единственное число K (1≤K≤50).

Выходные данные

Требуется вывести единственное число — наибольшее количество нерабочих дней, идущих подряд.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#111405

Ацтекская пирамида

Темы: [Формула]

Император ацтеков Куитлауак собирается построить пирамиду в свою честь. Эта пирамида должна быть выше, чем все предыдущие.

Ацтекская пирамида состоит из каменных блоков. Каждый блок это куб размерами 1 × 1 × 1. Куитлауак располагает первый блок на земле в процессе церемонии закладки пирамиды. Каждый следующий блок должен иметь общую грань с каким-нибудь из предыдущих блоков.

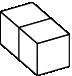
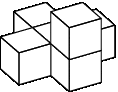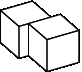
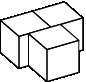
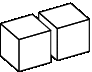
Правильные расположения блоков: $\text{[math]}$ $\text{[math]}$ Неправильные расположения блоков: $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Блок считается устойчивым, если он стоит на земле или на блоке, каждая грань которого соседствует с другим блоком или с землей. Чтобы пройти испытание временем, пирамида должна быть устойчивой, то есть все её блоки должны быть устойчивыми.

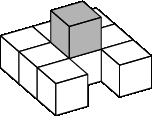
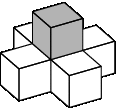
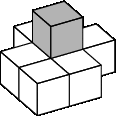
Устойчивые блоки: 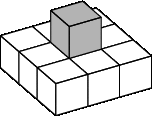$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ Неустойчивые блоки: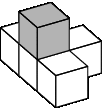 $\text{[math]}$ $\text{[math]}$

Куитлауак просит вас определить высоту самой высокой пирамиды, которую можно построить из имеющихся в наличии блоков.

Входные данные

Единственная строка входного файла содержит одно целое число n — количество имеющихся в наличии блоков, считая заложенный императором (1 ≤ n ≤ 10⁹).

Выходные данные

Выведите одно целое число — высоту самой высокой пирамиды, которую можно построить из имеющихся в наличии блоков.

Примеры тестов

Входные данные

Выходные данные

Входные данные

Выходные данные

Входные данные

Выходные данные

#112033

Берляндолимпстрой

Темы: [Двумерные массивы] [Формула]

Источники: [ Личные олимпиады, Открытая олимпиада школьников, 2012-2013, Заключительный этап - второй тур, Задача B ]

Скоро в Берляндии пройдет очередная Олимпиада. В рамках подготовки к этому важному мероприятию Берляндолимпстрой уже возвел N объектов и теперь хочет разобраться с тем, во сколько Берляндии это обошлось.

Стройка длилась $K + 1$ день со дня номер $0$ по день номер $K$, причем стоимость j-го объекта в нулевой день была равна $a_j$ бурлям. Однако каждый следующий день стоимость каждого объекта увеличивалась согласно следующему правилу: стоимость j-го объекта в i-й день становилась равна сумме стоимостей всех объектов с номерами, меньшими или равными j, в предыдущий день. Иначе говоря, $S_{i,j}$ = $\sum_{m=1}^{j} S_{i-1,m}$, где $S_{i,j}$ — стоимость j-го объекта в i-й день. В итоге на j-й объект было потрачено $S_{K,j}$ , то есть его стоимость в последний $K$-й день. \t{Назовем эту величину итоговой стоимостью j-го объекта.}

Такие увеличения стоимостей проектов для Берляндии не редкость, однако оказалось, что и этих денег не хватило! Выяснилось, что в некоторый день i > 0 стоимость некоторого объекта j дополнительно повысилась на пока не известную следователям сумму X (то есть $S_{i,j}$ = $\sum_{m=1}^{j} S_{i-1,m}$ + X), что повлияло на стоимости объектов в последующие дни. Следователи выяснили, что из-за этого сумма итоговых стоимостей всех объектов увеличилась на $R$ бурлей.

Помогите следователям выяснить минимально возможное значение X.

Входные данные

В первой строке входного файла содержатся три целых числа $N$, $K$, $R$: количество олимпийских объектов ($1 \le N \le 10^5$ ), количество дней увеличения стоимости объектов ($1 \le K \le 10^5$ ) и количество бурлей, на которое незаконно возросла итоговая сумма ($1 \le R \le 10^{18}$). В следующей строке входного файла содержатся N целых чисел $a_i$ — стоимости объектов в нулевой день ($1 \le a_i \le 10^9$).

Выходные данные

Единственная строка выходного файла должна содержать единственное целое число — минимально возможное значение $X$

Система оценки

Тесты к этой задаче состоят из четырех групп.

0. Тест 1. Тест из условия, оцениваемый в ноль баллов.

1. Тесты 2—25. В тестах этой группы $N \le 10, K \le 10, a_i \le 10$, искомое значение $X$ не превосходит $10$. Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.

2. Тесты 26—38. В тестах этой группы $N \le 1 000, K \le 1 000$. Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы. Решение будет тестироваться на тестах этой группы только в случае прохождения всех тестов первой группы.

3. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов. Тесты в этой группе оцениваются \t{независимо}

Примеры

Входные данные

3 3 12
1 3 3

Выходные данные

Страница: 1 2 3 4 >> Отображать по: