Как гласят старые малоярославские легенды, где-то далеко-далеко, где сборная России когда-то готовилась к международной олимпиаде, в одной из общеобразовательных школ живёт Граф. Ориентированность Графа, как следует из легенд, меняется от дня ко дню вместе с количеством вершин и ребер, что позволяет Графине и её отражению не скучать и играть во множество игр на Графе.
Вот уже многие дни Граф обрёл постоянную ориентированность; однако в последнее время Граф часто стал бывать раздражительным и колючим, и для Графини настали нелёгкие дни. Чтобы хоть как-то облегчить себе жизнь, Графиня решила написать программу, которая по текущему состоянию, то есть набору вершин и рёбер, сообщит Графине, является ли граф колючим. По опыту прошлых дней, Графиня заключила, что Граф является колючим, если и только если через любое его ребро проходит не более чем один простой цикл.
Напомним, что последовательность ребер ( u 1 , u 2 ) , ( u 2 , u 3 ) , ..., ( u k - 1 , u k ) , ( u k , u 1 ) является простым циклом, если вершины u 1 , u 2 , ..., u k попарно различны. Простой цикл проходит через ребро e , если ребро e содержится в последовательности ребер цикла.
Петлёй в графе называется ребро ( u , v ) , т.ч. u = v .
Рёбра ( u 1 , v 1 ) и ( u 2 , v 2 ) называются кратными, если u 1 = u 2 и v 1 = v 2 .
Помогите Графине понять, является ли её Граф, являющийся ориентированным графом без петель и кратных ребер, колючим или нет.
В первой строке записаны целые неотрицательные числа n и m ( 1 ≤ n ≤ 500 000 , 0 ≤ m ≤ 10 6 - количество вершин и рёбер графа-Графа.
Далее в следующих m строках записано по паре целых чисел u , v , 1 ≤ u , v ≤ n , u ≠ v .
Гарантируется, что в Графе не существует петель и кратных ребер.
Выведите слово " YES ", если Граф является колючим, и " NO " иначе.
3 3 1 2 2 3 3 1
YES
3 4 1 2 2 3 3 1 1 3
NO
У компании BigData Inc. есть n дата-центров, пронумерованных от 1 до n , расположенных по всему миру. В этих дата-центрах хранятся данные клиентов компании (как можно догадаться из названия — большие данные!)
Основой предлагаемых компанией BigData Inc. услуг является гарантия возможности работы с пользовательскими данными даже при условии выхода какого-либо из дата-центров компании из доступности. Подобная гарантия достигается путём использования двойной репликации данных. Двойная репликация — это подход, при котором любые данные хранятся в двух идентичных копиях в двух различных дата-центрах.
Про каждого из m клиентов компании известны номера двух различных дата-центров c i , 1 и c i , 2 , в которых хранятся его данные.
Для поддержания работоспособности дата-центра и безопасности данных программное обеспечение каждого дата-центра требует регулярного обновления. Релизный цикл в компании BigData Inc. составляет один день, то есть новая версия программного обеспечения выкладывается на каждый компьютер дата-центра каждый день.
Обновление дата-центра, состоящего из множества компьютеров, является сложной и длительной задачей, поэтому для каждого дата-центра выделен временной интервал длиной в час, в течение которого компьютеры дата-центра обновляются и, как следствие, могут быть недоступны. Будем считать, что в сутках h часов. Таким образом, для каждого дата-центра зафиксировано целое число u j ( 0 ≤ u j ≤ h - 1 ), обозначающее номер часа в сутках, в течение которого j -й дата-центр недоступен в связи с плановым обновлением.
Из всего вышесказанного следует, что для любого клиента должны выполняться условия u c i , 1 ≠ u c i , 2 , так как иначе во время одновременного обновления обоих дата-центров, компания будет не в состоянии обеспечить клиенту доступ к его данным.
В связи с переводом часов в разных странах и городах мира, время обновления в некоторых дата-центрах может сдвинуться на один час вперёд. Для подготовки к непредвиденным ситуациям руководство компании хочет провести учения, в ходе которых будет выбрано некоторое непустое подмножество дата-центров, и время обновления каждого из них будет сдвинуто на один час позже внутри суток (то есть, если u j = h - 1 , то новым часом обновления будет 0 , иначе новым часом обновления станет u j + 1 ). При этом учения не должны нарушать гарантии доступности, то есть, после смены графика обновления должно по-прежнему выполняться условие, что данные любого клиента доступны хотя бы в одном экземпляре в любой час.
Учения — полезное мероприятие, но трудоёмкое и затратное, поэтому руководство компании обратилось к вам за помощью в определении минимального по размеру непустого подходящего подмножества дата-центров, чтобы провести учения только на этом подмножестве.
В первой строке находятся три целых числа n , m и h ( 2 ≤ n ≤ 100 000 , 1 ≤ m ≤ 100 000 , 2 ≤ h ≤ 100 000 ) — число дата-центров компании, число клиентов компании и количество часов в сутках.
Во второй строке вам даны n чисел u 1 , u 2 , ..., u n ( 0 ≤ u j < h ), j -е из которых задаёт номер часа, в который происходит плановое обновление программного обеспечения на компьютерах дата-центра j .
Далее в m строках находятся пары чисел c i , 1 и c i , 2 ( 1 ≤ c i , 1 , c i , 2 ≤ n , c i , 1 ≠ c i , 2 ), задающие номера дата-центров, на которых находятся данные клиента i .
Гарантируется, что при заданном расписании обновлений в дата-центрах любому клиенту в любой момент доступна хотя бы одна копия его данных.
В первой строке выведите минимальное количество дата-центров k ( 1 ≤ k ≤ n ), которые должны затронуть учения, чтобы не потерять гарантию доступности. Во второй строке выведите k различных целых чисел — номера кластеров x 1 , x 2 , ..., x k ( 1 ≤ x i ≤ n ), на которых в рамках учений обновления станут проводиться на час позже. Номера кластеров можно выводить в любом порядке.
Если возможных ответов несколько, разрешается вывести любой из них. Гарантируется, что хотя бы один ответ, удовлетворяющий условиям задачи, существует.
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при про- хождении всех тестов группы и всех тестов предыдущих групп.

Рассмотрим первый тест из условия. Приведённый ответ является единственным способом провести учения, затронув только один дата-центр. В таком сценарии третий сервер начинает обновляться в первый час дня, и никакие два сервера, хранящие данные одного и того же пользователя, не обновляются в один и тот же час.
С другой стороны, например, сдвинуть только время обновления первого сервера на один час вперёд нельзя — в таком случае данные пользователей 1 и 3 будут недоступны в течение нулевого часа.
3 3 5 4 4 0 1 3 3 2 3 1
1 3
4 5 4 2 1 0 3 4 3 3 2 1 2 1 4 1 3
4 1 2 3 4
Центр Гдынии расположен на острове посередине реки Кацза. Каждое утро тысячи машин едут из жилых районов на западном берегу в индустриальные на восточном.
Остров можно представить в виде прямоугольника \(A\times B\) со сторонами, параллельными осям координат, углами \((0, 0)\) и \((A, B)\).
На острове есть \(n\) перекрёстков, пронумерованных натуральными числами от \(1\) до \(n\). Перекрёсток номер \(i\) имеет координаты \((x_i, y_i)\). Если координаты какого-то перекрёстка имеют вид \((0, y)\), то он находится на западном берегу, если \((A, y)\) - на восточном. Перекрёстки соединены дорогами, каждая - отрезок на плоскости, они не пересекаются (кроме концов). Дороги бывают односторонними и двусторонними. Нет никаких мостов и туннелей! Некоторые дороги могут идти по краям прямоугольника.
Поскольку плотность траффика растёт, мэр города нанял Вас (кого же ещё) проверить, достаточно ли текущей сети дорог. Он попросил написать программу, которая по карте города определит для каждого перекрёстка на западном берегу, сколько из него достижимых на восточном.
В первой строке входных данных дано четыре целых числа \(n\), \(m\), \(A\) и \(B\) (\(1\leq n\leq 300 000\), \(0\leq m\leq 900 000\), \(1\leq A\leq 10^9\), \(1\leq B\leq 10^9\). Это количества перекрёстков, дорог и размеры города, соответственно.
В каждой из следующих \(n\) строк есть два целых числа \(x_i\), \(y_i\) (\(0\leq x_i\leq A\), \(0\leq y_i\leq B\)), описывающих координаты перекрёстка номер \(i\). Перекрёстки не совпадают.
Следующие \(m\) строк описывают дороги, каждая одну. Это описание состоит из трёх чисел: \(c_i\) - номер перекрёстка, откуда (\(1\leq c_i\leq n\)), \(d_i\) - куда (\(1\leq d_i\leq n\)), \(k_i\in\{1, 2\}\) - тип дороги (сколькосторонняя). Разные дороги соединяют разные неупорядоченные пары перекрёстков.
Есть хотя бы один перекрёсткок на западном берегу, из которого можно добраться хотя бы в один на восточном по дорогам.
Выведите для каждого перекрёстка на западном берегу в своей строчке количество достижимых из него перекрёстков на восточном берегу.
Выводите в порядке уменьшения \(y\)-координаты.
1. (30 баллов) \(n, m\leq 6 000\).
2. (70 баллов) \(n\leq 300 000\), \(m\leq 900 000\).
5 3 1 3 0 0 0 1 0 2 1 0 1 1 1 4 1 1 5 2 3 5 2
2 0 2
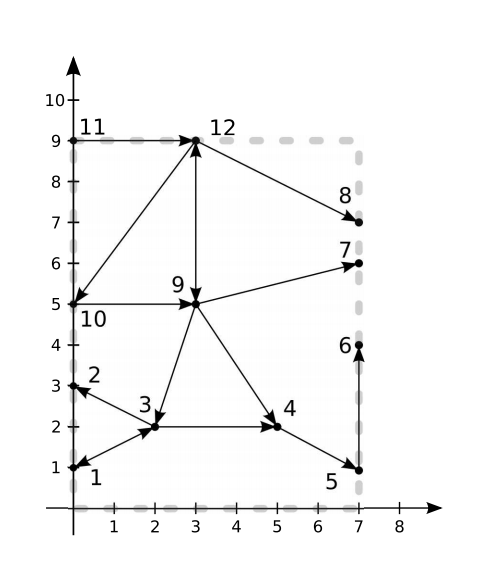
12 13 7 9 0 1 0 3 2 2 5 2 7 1 7 4 7 6 7 7 3 5 0 5 0 9 3 9 1 3 2 3 2 1 3 4 1 4 5 1 5 6 1 9 3 1 9 4 1 9 7 1 9 12 2 10 9 1 11 12 1 12 8 1 12 10 1
4 4 0 2