Рассмотрим ориентированный граф G, имеющий n вершин, пронумерованных натуральными числами от 1 до n. В графе G возможно наличие нескольких дуг между одной и той же парой вершин, а также дуг, ведущих из вершины в нее саму. Каждая дуга графа помечена некоторой буквой латинского алфавита. Каждому пути в графе G можно поставить в соответствии строку, состоящую из букв, написанных на последовательно проходимых в соответствии с этим путем дугах. Эта строка называется путевой меткой пути. Назовем строку
Ваша задача посчитать остаток от деления на 1 000 000 количества путевых строк графа G, состоящих ровно из L символов.
В первой строке входных данных записаны целые числа n, m, L (1 ≤ n ≤ 10, 1 ≤ m ≤ 10 000, 1 ≤ L ≤ 100), равные количеству вершин и ребер графа G, а также длине путевых строк, которые нужно искать. Следующие m строк задают дуги графа G. Каждая из этих строк содержит два натуральных числа a, b (1 ≤ a, b ≤ n) и маленькую латинскую букву c, что означает наличие дуги из вершины a в вершину b, помеченной символом c. Элементы каждой строки отделены друг от друга пробелами.
Единственная строка выходных данных должна содержать одно число, равное остатку от деления количества путевых строк длины L в графе G на 1 000 000.
4 4 100 1 2 a 2 3 b 3 4 a 4 1 b
2
Дан прямоугольник N x M, состоящий из квадратиков 1 x 1. Некоторые квадратики вырезали. Надо найти наименьшее количество прямоугольников, на которое можно разрезать оставшуюся фигуру.
В первой строке входных данных заданы числа N и M, (1 ≤ N, M ≤ 10). Далее следует N строк. В (i+1)-ой содержится M чисел; j-е число равно 1, если клетку на i-й строке и в j-м столбце вырезали из доски, 0 – если оставили.
Выведите единственное число – минимальное количество прямоугольников, на которое можно разрезать полученную фигуру.
2 2 0 0 1 0
2
Ограничение по времени: 3 секунды
Ограничение по памяти: 64 мегабайта
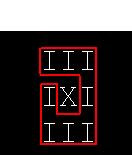
На этот раз Вася увлекся выращиванием арбузов. Его огород имеет форму прямоугольника \(N \times M\) метров, разделенного на одинаковые ячейки размером \(1 \times 1\) метр, в каждой из которых растет по арбузу. Как-то раз он решил осмотреть некоторые из них, начав в левом верхнем углу, пройдясь по огороду и вернувшись обратно. Ячейки, оказавшиеся внутри цикла, считаются осмотренными, остальные – не осмотренными. По некоторым банальным соображениям Вася не ходит по грядкам, а только лишь по специальным дорожкам, расположенным на границах ячеек с арбузами. Вдобавок, он хочет, чтобы его путь получился без самопересечений. К счастью, дорожки достаточно широкие для того, чтобы гулять по ним много раз, не считая это за самопересечение (см. рисунки к примерам).
Ваша задача – узнать, за какое минимальное время Васе удастся обойти ровно i арбузов. Можно считать, что он двигается равномерно со скоростью 1 метр в секунду.
Формат входных данных
В первой строке входных данных содержатся два числа \(N, M (1 \le N, M \le 50)\). В следующих N строках идет описание огорода. В (i + 1)-й строке содержатся M символов. Символ "I" на j-й позиции означает, что Вася хочет осмотреть арбуз, расположенный в i-й строке и j-м столбце огорода; символ " ." означает, что ему не важно, что происходит в соответствующей ячейке; символ "X" означает, что он не хочет осматривать это растение. Других символов в строке нет.
Гарантируется, что суммарное количество символов "I" и "X" не превосходит 10, и присутствует хотя бы один символ "I".
Формат выходных данных
Выведите ровно K чисел, разделенных пробелами, где K – количество арбузов, которые Вася хочет осмотреть (количество символов "I" во входном файле). Число номер i должно быть равно минимальному времени, за которое он успеет осмотреть ровно i арбузов, соответствующих символам "I".
Не забудьте учесть, что арбузы, помеченные ".", могут быть осмотрены или нет, но арбузы "X" Вася осматривать не хочет ни в коем случае.
Примеры
|
Входные данные |
Выходные данные |
|
1 1 |
4 |
|
2 2 |
8 |
|
3 3 |
4 6 8 10 12 14 16 18 |
|
3 3 |
8 10 14 |
|
1 10 |
4 6 12 14 20 26 28 |
По данному числу N выведите все строки длины N из нулей и единиц в лексикографическом порядке.
Задано единственное число N. (натуральное, 1 ≤ N ≤ 10)
Необходимо вывести все строки длины N из нулей и единиц в лексикографическом порядке, по одной на строке
2
00 01 10 11
По данному числу N выведите все строки длины N из нулей и единиц в обратном лексикографическом порядке.
Задано единственное число N. (1 ≤ N ≤ 10)
Необходимо вывести все строки длины N из нулей и единиц в обратном лексикографическом порядке.
2
11 10 01 00