Новый Президент Тридевятой республики начал свою деятельность с полной ревизии системы общественного транспорта страны. В результате на основе социологических опросов населения было составлено идеальное ежедневное расписание движения междугородних автобусов, утвержденное Парламентом республики.
Более того, было решено заменить весь автобусный парк одинаковыми новыми, очень дорогими, но гораздо более надежными, красивыми и удобными машинами.
Автобусная сеть страны охватывает N городов, занумерованных целыми числами от 1 до N.
Идеальное расписание содержит M ежедневных рейсов, i-й рейс начинается в городе Fi в момент времени Xi и заканчивается в некотором другом городе Gi в момент времени Yi. Продолжительность каждого рейса ненулевая и строго меньше 24 часов. Рейс i выполняется одним из автобусов, находящихся в момент времени Xi в городе Fi.
Новые автобусы не требуют ремонта и могут работать круглосуточно, поэтому автобус, прибывший в некоторый момент времени в некоторый город, всегда готов в тот же самый момент времени или позже отправиться в путь для обслуживания любого другого рейса из данного города. Автобус может выехать из города, только выполняя какой-либо рейс из расписания.
Предполагается, что расписание будет действовать неограниченное время, поэтому может оказаться так, что его невозможно обслужить никаким конечным числом автобусов.
Определите наименьшее количество новых автобусов, достаточное для обеспечения движения по расписанию в течение неограниченного периода времени.
В первой строке задаются целые числа N и М (1 ≤ N, M ≤ 100 000) — количество городов и рейсов автобусов соответственно.
В каждой из следующих M строк содержится описание рейса автобуса: номер города отправления Fi, время отправления Xi, номер города назначения Gi (Fi ≠ Gi), время прибытия Yi, отделенные друг от друга одним пробелом. Время прибытия и отправления задается в формате HH:MM, где HH — часы от 00 до 23, MM — минуты от 00 до 59.
Выведите одно число — минимально необходимое количество автобусов. Если расписание невозможно обслуживать в течение неограниченного периода времени конечным числом автобусов, выведите число -1.
4 6 1 10:00 2 12:00 1 10:00 3 09:00 3 12:00 4 23:00 2 11:00 4 13:00 4 12:00 1 11:00 4 12:00 1 10:30
8
Известный математик Соломон В. Голомб предложил название полимино для связной фигуры, вырезанной из клетчатой бумаги по линиям сетки. Фигура называется связной, если из любой ее клетки можно добраться в любую другую, переходя из клетки в клетку через их общую сторону. Шахматист, добавил Голомб, сказал бы, что из любой клетки полимино можно дойти ладьей в любую другую. На рис. 1 приведены примеры восьми полимино.
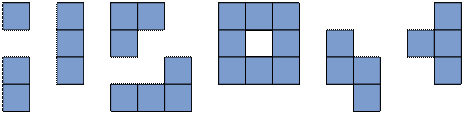
Рис. 1
Саша увлекается полимино. Для своих экспериментов она вырезает новое полимино из бумаги в клеточку или из старых полимино, оставшихся после предыдущих попыток. Далеко не всегда из старого полимино (рис. 2а, слева) можно вырезать новое (рис. 2а, справа). Поэтому Саша может перед вырезанием нового полимино разделить каждую клетку старого полимино на K2 одинаковых квадратных клеток меньшего размера (см. рис. 2б, здесь K = 2).
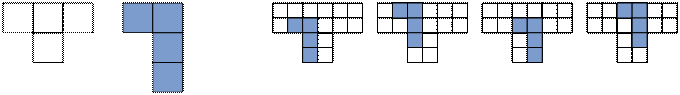
Рис. 2а Рис. 2б
Сашу заинтересовало, сколько существует различных способов вырезать новое полимино из старого при заданном значении K, если повороты, отражения и переворачивания как нового полимино, так и старого, недопустимы.
Например, на рис. 2б приведены все возможные способы вырезания полимино, приведенного на рис. 2а, при K = 2.
Напишите программу, которая ответит на интересующий Сашу вопрос.
Первая строка входных данных содержит число K (1 ≤ K ≤ 10 000).
Далее следуют описания двух полимино, сначала нового, затем старого. Каждое полимино задается следующим образом — в первой строке описания задаются размеры H (высота) и W (ширина) минимально возможного прямоугольника, в котором можно разместить данное полимино. Следующие Н строк содержат по W символов описания клеток. При этом клетка, входящая в полимино, обозначается символом « X» (прописная латинская буква «икс»), а не входящая — символом «.» (точка). Количество клеток в каждом полимино не превышает 300.
Выведите одно число — количество различных способов вырезать заданное новое полимино из старого, каждая клетка которого разбита на K2 клеток.
2 6 6 XXXXXX X....X X....X X....X X....X XXXXXX 5 5 XXXXX XXXXX XX.XX XXXXX XXXXX
9
Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.
Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.
Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.
Формат входных данных
В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.
Формат выходных данных
В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.
Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.
В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.
Если искомых разбиений несколько, выведите любое из них.
Примеры
-
Входные данные
Выходные данные
Рисунок к тесту
4
0 0
1 0
1 1
0 12
1
1 1 0 0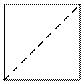
10
-6 0
0 2
6 0
3 3
6 4
2 4
0 6
-2 4
-6 4
-3 34
3
2 4 -2 4
0 2 3 3
-3 3 0 2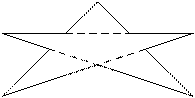
Сегодня в 5-А классе праздник — урок физкультуры. Традиционно ребята в это время после небольшой разминки играют в футбол. Коля очень любит футбол, но сегодня, проходя мимо учительской, он случайно услышал, что несколько самых сильных школьников из 5-А во время урока физкультуры должны помочь разгружать новые парты. Что же делать? Ведь Коля предпочитает поиграть в футбол!
В голове Коли моментально созрел план. Коля знает, что в 5-А классе N школьников. Он хочет воспользоваться тем, что учитель физкультуры Иван Петрович на уроках вместо обычной расстановки школьников в шеренгу по росту практикует расстановку «по силе». Для этого Иван Петрович сначала расставляет N школьников по росту, а затем (N – 1) раз проходит вдоль шеренги слева направо, каждый раз начиная с самого левого (первого) школьника и заканчивая предпоследним школьником справа. Проходя мимо школьника, который стоит на i-м месте (1 ≤ i ≤ N – 1), Иван Петрович просит его помериться силой с соседом справа, который стоит на (i + 1)-м месте. Если школьник, стоящий левее, оказывается сильнее своего соседа справа, то они меняются местами. Если же силы школьников оказываются равны, либо слева стоит более слабый школьник, то школьники остаются на своих местах. После этого Иван Петрович просит помериться силой школьников, стоящих на местах (i + 1) и (i + 2), и т. д., заканчивая каждый проход школьниками, которые стоят на местах (N – 1) и N. При любом сравнении «по силе» все школьники, включая Колю, показывают свою реальную силу, так как не хотят прослыть слабаками.
Для увеличения шансов поиграть в футбол, Коля хотел бы оказаться как можно левее в получившейся шеренге. Силу каждого из своих одноклассников он знает. По предыдущим занятиям Коля заметил, что если присесть «завязывать шнурки» при каком-либо из проходов учителя, то Иван Петрович во время такого прохода не будет просить Колю мериться силой ни с соседом слева, ни с соседом справа, и, тем более, не будет просить мериться силой соседей Коли, так как они не стоят рядом. Однако, чтобы сохранить силы для игры в футбол, Коля не может присесть более k раз.
Требуется написать программу, которая определит, как нужно действовать Коле, чтобы после проведения расстановки «по силе» оказаться в шеренге как можно левее.
В первой строке входных данных задаются три целых числа: N — число школьников в классе, p — место Коли в шеренге по росту, и k — количество приседаний, которое Коля может сделать, не потеряв при этом способность играть в футбол (2 ≤ N ≤ 100 000, 1 ≤ p ≤ N, 1 ≤ k ≤ N – 1).
Во второй строке задаются целые числа a1, a2, ..., aN (1 ≤ ai ≤ 109). Число ai показывает силу школьника, который стоит на i-м месте по росту. Школьник, который стоит на i-м месте в расстановке по росту, сильнее школьника, который стоит j-м месте в расстановке по росту, если ai > aj.
В первой строке выведите самую левую позицию в шеренге, в которой может оказаться Коля после построения школьников «по силе». Во второй строке выведите любую из возможных стратегий Коли, приводящую к этому результату. Стратегия выводится в виде строки из (N – 1) символов, j-й символ этой строки должен быть равен символу «+», если на j-м проходе Коле необходимо присесть, и символу «-» — в противном случае.
Примечание
Решения, корректно работающие при N ≤ 3000, будут оцениваться, исходя из 70 баллов.
10 5 6 10 1 8 3 6 5 4 7 2 9
5 ---++++++
На пригородной железной дороге N станций и M соединяющих их перегонов. Любые две станции соединены не более чем одним перегоном. Сеть перегонов устроена так, что, отправившись от любой станции, можно вернуться на нее, только проехав хотя бы один перегон дважды. На железной дороге организовано движение электричек. Каждая электричка ходит в обоих направлениях по своему маршруту между двумя конечными станциями и останавливается на всех промежуточных станциях
Для удобства пассажиров руководство железной дороги решило ввести новую систему оплаты проезда. По этой системе каждой станции присваивается некоторое целое число, называемое тарифным номером этой станции. Стоимость проезда между двумя станциями без пересадок определяется модулем разности тарифных номеров этих станций. Тарифные номера станций вдоль маршрута каждой электрички должны изменяться монотонно, то есть при движении в каком-либо направлении строго возрастать и, следовательно, строго убывать при движении в обратном направлении. Это обеспечивает рост стоимости проезда с увеличением количества пройденных перегонов.
Требуется написать программу, которая назначит каждой станции тарифный номер.
|
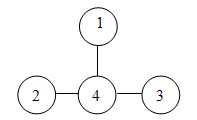
|
4 станции, 3 перегона: 1-4, 2-4, 3-4 Маршруты: 1-4-2, 2-4-3, 3-4-1. Ответ: решения нет |
|
|
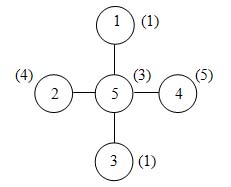
5 станций, 4 перегона: 1-5, 2-5, 3-5, 4-5 Маршруты: 1-5-2, 2-5-3, 3-5-4, 4-5-1. Ответ: решение есть; например, следующее: номер станции: 1 2 3 4 5 тарифный номер: 1 4 1 5 3 Замечание: тарифные номера разных станций могут совпадать. |
В первой строке входных данных содержатся два целых числа: N — количество станций (2 ≤ N ≤ 100 000), и M — количество перегонов между ними (1 ≤ M ≤ N – 1). В последующих M строках записаны пары целых чисел a, b (a ≠ b, 1 ≤ a ≤ N, 1 ≤ b ≤ N), означающие наличие перегона между станциями a и b. За ними в отдельной строке записано единственное целое положительное число K — количество маршрутов электричек. В последующих K строках идут описания маршрутов электричек, по одному на строке. Каждое описание представляет собой последовательность целых чисел — номеров всех станций маршрута в порядке одного из двух возможных направлений следования электрички. Описание маршрута заканчивается числом 0.
Все номера станций в описании маршрута различны. Количество станций в каждом маршруте не менее двух. Любые две последовательные станции в маршруте каждой электрички соединены перегоном. Суммарное количество станций в описаниях всех маршрутов не превосходит 200 000. Могут быть станции и перегоны, через которые не проходит ни одна электричка.
В первую строку выведите «NO», если искомого назначения тарифных номеров не существует. В противном случае в первую строку выведите «YES», а в следующей строке — N целых положительных чисел, где i-е число — тарифный номер i-й станции. Тарифный номер каждой станции должен находиться в диапазоне от 1 до N.
Если существует несколько решений, необходимо вывести любое из них.
Система оценивания
Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
- Группа 1 (20 баллов): N, K <= 20
- Группа 2 (30 баллов): N, K <= 2000
- Группа 3 (50 баллов): без дополнительных ограничений
6 5 1 2 5 2 5 6 4 5 3 2 6 1 2 0 5 6 0 3 2 1 0 5 2 3 0 4 5 2 0 6 5 4 0
YES 2 3 4 1 2 3