В Волшебной стране используются монетки достоинством A1, A2,…, AM. Волшебный человечек пришел в магазин и обнаружил, что у него есть ровно по две монетки каждого достоинства. Ему нужно заплатить сумму N. Напишите программу, определяющую, сможет ли он расплатиться без сдачи.
Сначала вводится число N (1≤N≤109), затем — число M (1≤M≤15) и далее M попарно различных чисел A1, A2,…, AM (1≤Ai≤109).
Выведите сначала K — количество монет, которое придется отдать Волшебному человечку, если он сможет заплатить указанную сумму без сдачи. Далее выведите K чисел, задающих достоинства монет. Если решений несколько, выведите вариант, в котором Волшебный человек отдаст наименьшее возможное количество монет. Если таких вариантов несколько, выведите любой из них.
Если без сдачи не обойтись, то выведите одно число 0. Если же у Волшебного человечка не хватит денег, чтобы заплатить указанную сумму, выведите одно число –1 (минус один).
Оценка задачи
1 балл получат программы, правильно решающие задачу с дополнительными ограничениями Ai≤106, M≤10.
5 2 1 2
3 2 2 1
7 2 1 2
-1
5 2 3 4
0
В компании MacroHard в последнее время резко участились опоздания сотрудников. Проанализировав ситуацию, руководство решило, что это вызвано большим разбросом в показаниях наручных часов сотрудников. После дополнительного совещания руководящего состава было постановлено, что все сотрудники должны перевести часы на одно и то же время (не важно какое).
Все сотрудники компании носят исключительно электронные часы одного образца. Время на них отображается в формате HH:MM:SS (где HH — часы, MM — минуты, SS — секунды, всегда отображаются в виде двух цифр, 00≤HH≤23, 00≤MM≤59, 00≤SS≤59). Перевод часов осуществляется с помощью двух кнопок. Первая кнопка меняет поле редактирования следующим образом: после первого нажатия часы переходят из режима отображения времени в режим редактирования поля HH, после второго — в режим редактирования поля MM, после третьего — в режим редактирования поля SS, а после четвертого возвращаются в режим отображения времени и т.д. по циклу. Каждое нажатие второй кнопки приводит к увеличению редактируемого поля на единицу (в режиме отображения времени ничего не происходит). При переполнении секунд поле SS обнуляется, а MM увеличивается на единицу, при переполнении минут поле MM обнуляется, а HH увеличивается на единицу, а при переполнении часов просто обнуляется поле HH.
И все бы хорошо, но, в силу своей природной лени, сотрудники хотят минимизировать суммарное число нажатий кнопок при переводе часов. При этом после перевода часов все часы должны оказаться в режиме отображения времени, в начале все часы также находятся в этом режиме.
Напишите программу, определяющую минимальное суммарное количество нажатий кнопок, достаточное для перевода часов всеми сотрудниками к одному времени.
Первая строка входных данных содержит натуральное число N (1≤N≤200) — количество сотрудников компании. Последующие N строк содержат показания часов каждого из сотрудников в формате "HH:MM:SS".
Выведите одно число — минимальное суммарное количество нажатий.
Система оценки 1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤2.
2 08:01:01 07:59:00
7
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
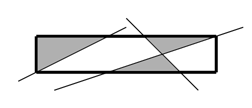
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала на вход программы поступают два положительных числа X и Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее вводится целое число N — количество разрезов (1≤N≤200). Затем описываются сами разрезы. Каждый разрез делался вдоль некоторой прямой. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все входные данные (кроме N) – вещественные числа, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число — количество частей исходного прямоугольника, имеющих треугольную форму.
Система оценки
1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤50.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4
Рассмотрим фигуру, аналогичную показанной на рисунке (большой равносторонний треугольник, составленный из маленьких равносторонних треугольников). На рисунке приведена фигура, состоящая из 4-х уровней треугольников.
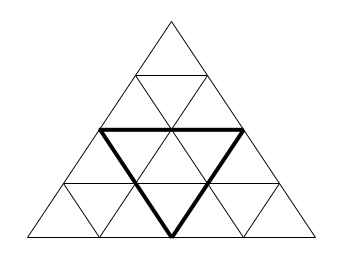
Напишите программу, которая будет определять, сколько всего в ней треугольников (необходимо учитывать не только "маленькие" треугольники, а вообще все треугольники — в частности, треугольник, выделенный жирным, а также вся фигура, являются интересующими нас треугольниками).
Вводится одно число \(N\) — количество уровней в фигуре (\(1\le N \le 100000\)).
Выведите количество треугольников в такой фигуре.
1
1
2
5
4
27
Пусть a1 = 2, a2 = 3, an = a1∙a2∙...∙an-1 – 1 при n ≥ 3. Назовем числа ai псевдопростыми. Для заданного натурального числа X нужно ответить на вопрос: можно ли X однозначно представить в виде произведения псевдопростых чисел (представления, отличающиеся только порядком множителей, считаются одинаковыми), и, если можно — выдать разложение.<
Вводится одно натуральное число X, 1 < X ≤ 109.
Выведите псевдопростые числа, произведение которых равно X, в произвольном порядке. Если разложения не существует или оно не единственно, выдать 0.
Оценка задачи
1 балл будет набирать программа, верно работающая для X ≤ 100.
6
2 3
5
5
7
0