Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 124 125 126 127 128 129 130 >> Отображать по:
#721
Шнурки
  
Темы: [Целые числа]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N.

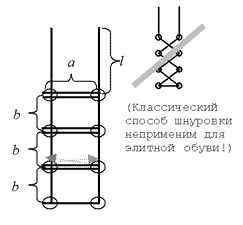Рис. 1 Шнуровка должна происходить элитным способом «наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.» (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l.

Какова должна быть длина шнурка для этих ботинок?

Входные данные

Вводятся четыре натуральных числа a, b, l и N.

Выходные данные

Ваша программа должна выводить одно число – искомую длину шнурка.

Примеры
Входные данные
2 1 3 4
Выходные данные
26
#722
Пересадки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На Новом проспекте для разгрузки было решено пустить два новых автобусных маршрута на разных участках проспекта.  Известны конечные остановки каждого из автобусов. Определите количество остановок, на  которых можно пересесть с одного автобуса на другой.

Входные данные

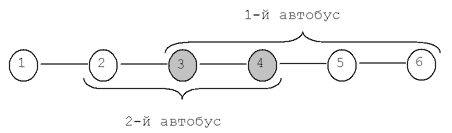
Вводятся четыре числа, не превосходящие 100, задающие номера конечных остановок. Сначала для первого, потом второго автобуса (см. примеры и рисунок).

Выходные данные

Ваша программа должна выводить одно число – искомое количество остановок.

 Задача В, рис. 2

Пояснения

Первый пример (см. рисунок): первый автобус ходит с 3-й остановки по 6-ю и обратно, а второй с 2-й по 4-ю и обратно. Пересесть с одного автобуса на другой можно на 3-й и 4-й остановках. Их две.

Второй пример: автобусы не имеют общих остановок.

Примеры
Входные данные
3 6 4 2
Выходные данные
2
Входные данные
3 1 5 10
Выходные данные
0
#723
Метод бутерброда
  
Темы: [Строки]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

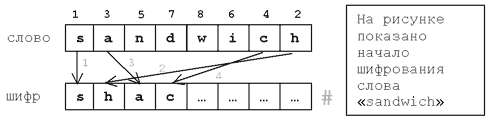
Секретное агентство «Super-Secret-no» решило для шифрования переписки своих сотрудников использовать «метод бутерброда». Сначала буквы слова нумеруются в таком порядке: первая буква получает номер 1, последняя буква - номер 2, вторая – номер 3, предпоследняя – номер 4, потом третья … и так для всех букв (см. рисунок). Затем все буквы записываются в шифр в порядке своих номеров. В конец зашифрованного слова добавляется знак «диез» (#), который  нельзя использовать в сообщениях.

Например, слово «sandwich» зашифруется в «shacnidw#».

 Задача С, рис. 3

К сожалению, программист «Super-Secret-no», написал только программу шифрования и уволился. И теперь агенты не могут понять, что же они написали друг другу. Помогите им.

Входные данные

Вводится слово, зашифрованное методом бутерброда. Длина слова не превышает 20 букв.

Выходные данные

Выведите расшифрованное слово.

Примеры
Входные данные
Aabrrbaacda#
Выходные данные
Abracadabra
#724
Берляндия атакует
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В этой задаче Вам вновь придется помочь Берляндии. Эта страна состоит из \(n\) городов, некоторые пары из которых соединены двусторонними дорогами, каждая дорога характеризуется своей длиной. Все города пронумерованы числами от 1 до \(n\), столица имеет номер 1. Время от време ни Президент объезжает страну, посещая города страны. Целью каждой поездки является один из городов, к которому он едет из столицы вдоль дорог одним из кратчайших путей.

В далекие времена (когда задачи на алгоритм Дейкстры вызывали сложность) специальное ведомство составила такой набор дорог \(T\), вдоль которого можно было проехать из столицы в любой город, причем единственным образом. Разумеется, путь по дорогам из набора \(T\) из столицы в каждый город являлся кратчайшим. Особо умные жители страны попросту называли этот набор дорог "деревом кратчайших путей". Известно, что Президент пользовался дорогами из \(T\) во время своих поездок. За прошедшие годы этот набор перестал быть секретным, и, поэтому, стал объектом повышенного внимания берляндских экстремистов. У специального ведомства новое задание. Для каждого города кроме столицы необходимо вычислить кратчайшее расстояние до него, при условии, что та дорога по которой Президент должен был закончить свой путь в этот город является атакованной и проезжать по ней нельзя.

Входные данные

В первой строке входного файла записана пара целых чисел \(n\) и \(m\) (\(2 \leq n \leq 4\,000\); \( n - 1 \leq m \leq 100\,000\)), где \(n\) — количество городов в стране, а \(m\)— количество дорог в этой стране. Далее в \(m\) строках содержатся описания дорог, по одной дороге в строке. Каждая дорога задается четверкой целых чисел \(a_j\), \(b_j\), \(l_j\), \(t_j\) , где \(a_j\), \(b_j\) это номера городов, соединяемых дорогой (\(1 \leq a_j, b_j \leq n\); \(a_j \neq b_j\)), \(l_j\) — ее длина (\(1 \leq l_j \leq 10^5\)), а \(t_j\) равно 1 если дорога принадлежит дереву кратчайших путей и 0 в противном случае.

Гарантируется, что набор \(T\) удовлетворяет описанным выше свойствам. Между парой городов может быть более одной дороги. Все дороги двусторонние.

Выходные данные

Выведите \(n - 1\) число в строку через пробелы. \(i\)-ое число должно быть равно либо длине кратчайшго пути из столицы в город \(i + 1\), при условии, что по той дороге из \(T\), которой Президент заканчивал свой путь в этот город, передвигаться нельзя, либо -1, если добраться до города \(i + 1\) вообще невозможно.

Примеры
Входные данные
5 9
3 1 3 1
1 4 2 1
2 1 6 0
2 3 4 0
5 2 3 0
3 2 2 1
5 3 1 1
3 5 2 0
4 5 4 0
Выходные данные
6 7 8 5
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

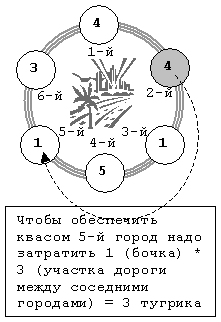
Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
Страница: << 124 125 126 127 128 129 130 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест