Страница: << 149 150 151 152 153 154 155 >> Отображать по:

#954

Сад пчел

Темы: [Обход в глубину] [Элементарная геометрия]

В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.

Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.

Входные данные

На вход сначала подается число n — количество ульев ($1 \leq n \leq 200$).

Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих $n$ строках входных данных записаны координаты ульев в саду Бена. Они не превосходят $10000$ по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от $1$ до $n$.

Следующие $n$ строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.

Выходные данные

Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.

Примеры

Входные данные

Выходные данные

0 3

#955

Преобрзование матрицы

Темы: [Двумерные массивы]

Введем следующие операции надо прямоугольной таблицей символов. Пусть нам дана матрица $А$, состоящая из $m$ строк (первый индекс) и $n$ столбцов (второй индекс). Определим результирующую матрицу $В$ для каждой из операций следующим образом:

Транспозиция относительно главной диагонали (код операции '1'): $B_{j,i}=A_{i,j}$
Транспозиция относительно другой диагонали (код операции '2'): $B_{n-j+1,m-i+1}=A_{i,j}$
Горизонтальное отражение (код операции 'H'): $B_{m-i+1,j}=A_{i,j}$
Горизонтальное отражение (код операции 'V'): $B_{i,n-j+1}=A_{i,j}$
Поворот на 90 ('A'), 180 ('B'), или 270 ('C') градусов по часовой стрелке: $B_{j,m-i+1}=A_{i,j}$ (для $90^{\circ}$)
Поворот на 90 ('X'), 180 ('Y'), или 270 ('Z') градусов против часовой стрелки: $B_{n-j+1,i}=A_{i,j}$ (для $90^{\circ}$)

Вам дана последовательность не более $100000$ операций над исходной матрицей. Выведите полученную в результате этих операций матрицу.

Входные данные

В первой строке входных данных находятся значения $m$ и $n$ ($0 < m, n \leq 300$). В каждой из следующих $m$ строк находятся по $n$ печатных символов (т.е. не используются символы с кодами от 33 до 126).

Последняя строка содержит описание операций, которые были выполнены над этой матрицей, путем записи без пробелов из кодов. Операции выполняются по порядку слева направо.

Выходные данные

Выведите сначала два целых числа $-$ число строк и столбцов в результирующей матрице. Затем выведите саму матрицу в том же формате, что и во входных данных.

Примеры

Входные данные

3 4
{uf=
v-fn
("C%
1

Выходные данные

4 3
{v(
u-"
ffC
=n%

#957

Даша и кризис

Темы: [Бинарный поиск по ответу]

Даша имеет $n$ ювелирных украшений. Каждое украшение имеет стоимость $w_i$ и значимость для Даши $v_i$. В связи с финансовым кризисом Даша решила продать некоторые украшения и сохранить только $k$ из имеющихся. Чтобы решить, что именно сохранить, Даша вводит параметр важности для набора из выбранных $k$ украшений, который вычисляет по следующей формуле:

$\frac{\sum_{j=1}^k v_i}{\sum_{j=1}^k w_i}$

Даша решает сохранить такие $k$ украшений, для которых параметр важности будет максимально возможным. Помогите ей правильно выбрать украшения.

Входные данные

Первая строка ввода содержит числа $n$ – количество ювелирных изделий у Даши и $k$ – количество ювелирных изделий, которые планируется оставить $ (1 \leq k \leq n \leq 100\,000) $.

В следующих $n$ строках содержатся по два числа – $v_i$ и $w_i (0 \leq v_i \leq 10^6, 1 \leq w_i \leq 10^6$, обе суммы всех значений $v_i$ и $w_i$ не превосходят $10^7$ каждая).

Выходные данные

Выведите $k$ чисел – номера ювелирных украшений, которые следует оставить. Если существует несколько решений, то выведите любое из них.

Примеры

Входные данные

Выходные данные

1
2

#961

Фен шуй

Темы: [Многоугольники. Выпуклые оболочки]

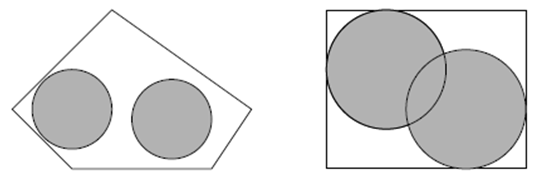
Фен шуй – это древняя китайская практика размещения предметов в пространстве для достижения гармонии. В ней говорится, что пол не должен быть пустым, поэтому Фил разместил на полу два одинаковых круглых ковра (по фен шуй надо избегать прямых линий и острых углов).

К сожалению, ими нельзя покрыть пол комнаты полностью, так как она имеет форму выпуклого многоугольника. Фил хочет минимизировать непокрытую часть пола, располагая ковры оптимальным образом.

Помогите ему расположить два ковра в комнате так, чтобы общая покрытая площадь была максимальна. Ковры можно накладывать друг на друга, но их нельзя загибать и резать.

Входные данные

Первая строка входных данных содержит два целых числа $n$ и $r$ — число углов в комнате $(3 \le n \le 100)$ и радиус ковров ($1 \le r \le 1000$, оба ковра имею один и тот же радиус). Следующие n строк содержат по два числа $x_i$ и $y_i$ — координаты $i$-го угла \((–1000 \le x_i; y_i \le 1000). Углы описаны в порядке обхода комнаты по часовой стрелке. Координаты углов различны и соседние стены не коллинеарны.

Выходные данные

Выведите \)x_1, y_1, x_2, y_2$, где $(x_1, y_1)$ и $(x_2, y_2)$ обозначаю центры ковров. Координаты должны иметь точность не менее 4 цифр после точки. Выведите любое оптимальное расположение. Входные данные гарантируют, что решение существует (Фил не стал бы покупать ковер, который не помещается в комнату).

Примеры

Входные данные

Выходные данные

-2.1715728753 3.0000000000 4.2617090669 2.4981148759

Входные данные

Выходные данные

3.0000000000 5.0000000000 7.0000000000 3.0000000000

#963

Японский кроссворд

Темы: [Бинарный поиск по ответу]

Наиболее известная игра, дошедшая до нас из Японии – это Судоку. Новая игра должна затмить ее славу. Про нее известно следующее. Нам дан квадрат, разделенный сеткой на n×n клеток, а каждая клетка содержит картинку одного из k типов. Игрок должен переместить их, чтобы получить максимально возможное число одинаковых первых рядов (два ряда считаются одинаковыми, если оба заполнены одинаковыми картинками и в одинаковом порядке). По виду таблицы определите, сколько одинаковых рядов в ней можно сложить (если менять картинки как угодно).

Например, если нам дана такая таблица:

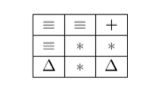
одно из результирующих состояний в игре будет

Входные данные

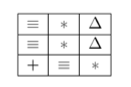
Первая строка входных данных содержит два числа n ($1\leq n \leq 40000$) и k ($1 \leq k \leq 50000$). Каждая из следующих k строк содержит число картинок в таблице каждого из k типов. Все числа больше 0, их сумма в точности равна $n^2$.

Выходные данные

Выведите в первой строке максимальное количество одинаковых рядов, которые можно построить из этих картинок. В следующих n строках выведите содержание таких рядов: в каждой строке должно находиться одно число – номер соответствующей картинке в порядке ее появления во входных данных. Если решений несколько, выведите любое из них.

Примеры

Входные данные

Выходные данные

Страница: << 149 150 151 152 153 154 155 >> Отображать по:

Выбрано

Отменить

Добавить в контест